
3、此时北京时间是
A、6月22日4时 B、6月23日2时
C、12月22日2时 D、6月21日13时
2、如果此时北京时间为6月22日14点,关于图
中A、B两点说法正确的是
 A、A所在国著名的人文景观有大金塔
A、A所在国著名的人文景观有大金塔
B、A所在地吹西南风,附近盛产黄麻
C、B处附近洋流为寒流,并由东向西流动
D、B处附近洋流为暖流,并由西向东流动
下图为某日太阳高度分布示意图,图中AB所在纬线为赤道,CD为经线圈,C经度为西经90度。回答下列问题:
1、图中a、b两条等太阳高度线上的太阳高度分别是
A、30°、60° B、60°、30°
C、23°26′、66°34′ D、66°34′、23°26′
10. 某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率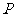 与日产量
与日产量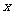 (件)之间大体满足关系:
(件)之间大体满足关系:
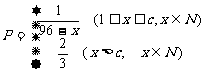 (其中c为小于96的正常数)
(其中c为小于96的正常数)
注:次品率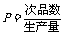 ,如
,如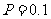 表示每生产10件产品,约有1件为次品.其余为合格品.
表示每生产10件产品,约有1件为次品.其余为合格品.
已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损 元,故厂方希望定出合适的日产量.
元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器每天的盈利额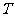 (元)表示为日产量
(元)表示为日产量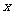 (件)的函数;
(件)的函数;
(2)当日产量为多少时,可获得最大利润?
讲解 (1)当 时,
时,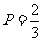 ,所以,每天的盈利额
,所以,每天的盈利额 ;
;
当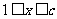 时,
时,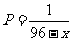 ,所以,每日生产的合格仪器约有
,所以,每日生产的合格仪器约有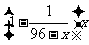 件,次品约有
件,次品约有 件.故,每天的盈利额
件.故,每天的盈利额
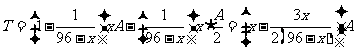 .
.
综上,日盈利额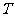 (元)与日产量
(元)与日产量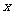 (件)的函数关系为:
(件)的函数关系为:

(2)由(1)知,当 时,每天的盈利额为0.
时,每天的盈利额为0.
当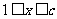 时,
时,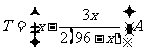 .
.
令 ,则
,则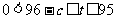 .故
.故
 .
.
当且仅当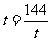 ,即
,即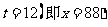 时,等号成立.
时,等号成立.
所以(i)当 时,
时,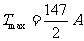 (等号当且仅当
(等号当且仅当 时成立).
时成立).
(ii)
当 时,由
时,由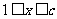 得
得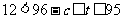 ,
,
易证函数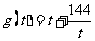 在
在 上单调递增(证明过程略).
上单调递增(证明过程略).
所以,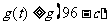 .所以,
.所以,
 即
即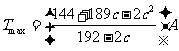 .(等号当且仅当
.(等号当且仅当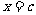 时取得)
时取得)
综上,若 ,则当日产量为88件时,可获得最大利润;若
,则当日产量为88件时,可获得最大利润;若 ,则当日产量为
,则当日产量为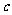 时,可获得最大利润.
点评:分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
时,可获得最大利润.
点评:分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
[探索题](2006福建)已知函数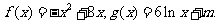
(I)求 在区间
在区间 上的最大值
上的最大值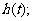
(II)是否存在实数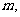 使得
使得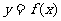 的图象与
的图象与 的图象有且只有三个不同的交点?若存在,求出
的图象有且只有三个不同的交点?若存在,求出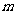 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
解:(I)
当 即
即 时,
时, 在
在 上单调递增,
上单调递增,
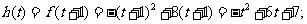
当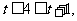 即
即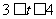 时,
时,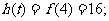
当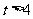 时,
时, 在
在 上单调递减,
上单调递减,

综上,
(II)函数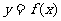 的图象与
的图象与 的图象有且只有三个不同的交点,即函数
的图象有且只有三个不同的交点,即函数
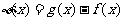 的图象与
的图象与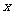 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。

当 时,
时, 是增函数;
是增函数;
当 时,
时,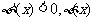 是减函数;
是减函数;
当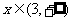 时,
时, 是增函数;
是增函数;
当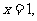 或
或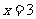 时,
时,
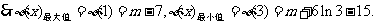
 当
当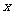 充分接近0时,
充分接近0时,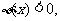 当
当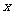 充分大时,
充分大时,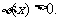
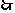 要使
要使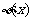 的图象与
的图象与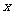 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
 即
即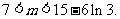
所以存在实数m,使得函数y =f(x)与y=g(x)的图象有且只有三个不同的交点,m的取值范围为(7,15-ln3)
9. (2005浙江)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
(Ⅲ)若h(x)=g(x)-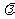 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数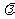 的取值范围.
的取值范围.
解:(I)设函数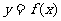 的图象上任一点
的图象上任一点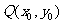 关于原点的对称点为
关于原点的对称点为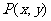 ,
,
则 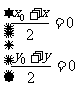 即
即
 .
.
∵点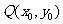 在函数
在函数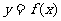 的图象上.
的图象上.
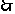
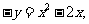 即
即 故g(x)=
故g(x)=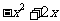 .
.
(II)由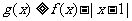 可得:
可得: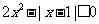
当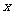
 1时,
1时,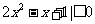
此时不等式无解。
当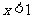 时,
时,
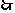
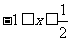
因此,原不等式的解集为[-1,  ].
].
(III) 
①
当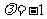 时,
时,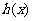 =
=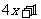 在[-1,1]上是增函数,
在[-1,1]上是增函数,
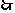
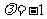
②当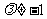 时,对称轴的方程为
时,对称轴的方程为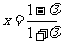
(i) 当 时,
时,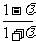
 ,解得
,解得 。
。
(ii) 当 时,
时,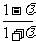
 1时,解得
1时,解得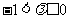
综上,
8.设A={x||x|=kx+1},若A∩R+=φ,A∩R-≠φ,求实数k的取值范围.
解法1:方程|x|=kx+1的解是函数y=|x|和y=kx+1交点的横坐标,结合图形知,当直线y=kx+1在α范围内时,方程有负根,且没有正根,故k≥1.
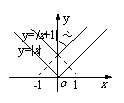 解法2:由题意须
解法2:由题意须 ①有解,
①有解,
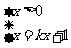 ②无解.
②无解.
①中k=-1时无解,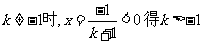 ;
;
②中k=1时无解,k≠0时,若 则②有解,
则②有解,
所以, k≥1.
7.求函数 的反函数。
解:∵ f(x)在R上是单调减函数, ∴ f(x)在R上有反函数。
∵ y=x2+1(x≤0)的反函数是
的反函数。
解:∵ f(x)在R上是单调减函数, ∴ f(x)在R上有反函数。
∵ y=x2+1(x≤0)的反函数是 (x≥1),
y=1-x(x>0)的反函数是y=1-x(x<1),
∴ 函数f(x)的反函数是
(x≥1),
y=1-x(x>0)的反函数是y=1-x(x<1),
∴ 函数f(x)的反函数是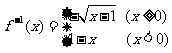 注 :求分段函数的反函数只要分别求出其反函数即可。
注 :求分段函数的反函数只要分别求出其反函数即可。
6.已知函数f(x)=|x2-2x-3|的图象与直线y=a有且仅有3个交点,则a= 。
简答提示:1-3. C DA; 4.分段解取并集{x|x≤1}; 5.(-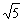 ,+∞);6. 由图象易知a=4。
,+∞);6. 由图象易知a=4。
[解答题]
5.(2005北京东城模拟)定义“符号函数”f(x)=sgnx=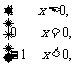 则不等式x+2>(x-2)sgnx的解集是______________.
则不等式x+2>(x-2)sgnx的解集是______________.
4.已知f(x)=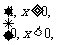 则不等式xf(x)+x≤2的解集是________________.
则不等式xf(x)+x≤2的解集是________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com