
77.(2009年新疆乌鲁木齐市)有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元.依此类推,即每多买一台则所买各台单价均再减20元,但最低不能低于每台440元;乙公司一律按原售价的75%促销.某单位需购买一批图形计算器:
(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?
(2)若此单位恰好花费7 500元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?
76.(09湖南邵阳)如图(十二),直线 的解析式为
的解析式为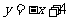 ,它与
,它与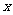 轴、
轴、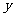 轴分别相交于
轴分别相交于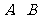 两点.平行于直线
两点.平行于直线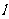 的直线
的直线 从原点
从原点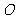 出发,沿
出发,沿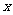 轴的正方形以每秒1个单位长度的速度运动,它与
轴的正方形以每秒1个单位长度的速度运动,它与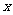 轴、
轴、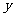 轴分别相交于
轴分别相交于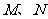 两点,设运动时间为
两点,设运动时间为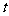 秒(
秒(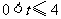 ).
).
(1)求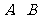 两点的坐标;
两点的坐标;
(2)用含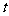 的代数式表示
的代数式表示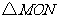 的面积
的面积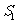 ;
;
(3)以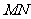 为对角线作矩形
为对角线作矩形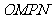 ,记
,记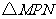 和
和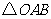 重合部分的面积为
重合部分的面积为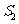 ,
,
①当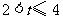 时,试探究
时,试探究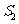 与
与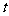 之间的函数关系式;
之间的函数关系式;
②在直线 的运动过程中,当
的运动过程中,当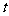 为何值时,
为何值时,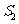 为
为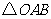 面积的
面积的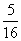 ?
?
75.(2009年山西省)解方程: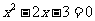
74.(2009年广东省)某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
73.(2009年潍坊)要对一块长60米、宽40米的矩形荒地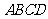 进行绿化和硬化.
进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形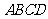 面积的
面积的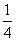 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为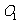 和
和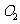 ,且
,且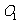 到
到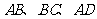 的距离与
的距离与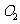 到
到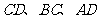 的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
72.(2009年宁波市)2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年投入6000万元用于改善医疗卫生服务,比2008年增加了1250万元.投入资金的服务对象包括“需方”(患者等)和“供方”(医疗卫生机构等),预计2009年投入“需方”的资金将比2008年提高30%,投入“供方”的资金将比2008年提高20%.
(1)该市政府2008年投入改善医疗卫生服务的资金是多少万元?
(2)该市政府2009年投入“需方”和“供方”的资金各多少万元?
(3)该市政府预计2011年将有7260万元投入改善医疗卫生服务,若从2009~2011年每年的资金投入按相同的增长率递增,求2009~2011年的年增长率.
71.(2009年中山)某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
70. (2009年湖州)随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1) 若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆?
(2) 为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
68.(2009年兰州)用配方法解一元二次方程:
[关键词]解一元二次方程的配方法
[答案]解:移项,得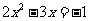 ,二次项系数化为1,得
,二次项系数化为1,得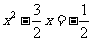
配方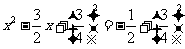 ,
,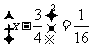 ,由此可得
,由此可得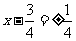 ,
,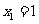 ,
,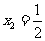
69(2009年包头)某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量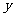 (件)与销售单价
(件)与销售单价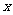 (元)符合一次函数
(元)符合一次函数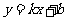 ,且
,且 时,
时,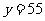 ;
;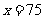 时,
时,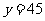 .
.
(1)求一次函数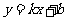 的表达式;
的表达式;
(2)若该商场获得利润为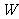 元,试写出利润
元,试写出利润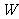 与销售单价
与销售单价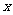 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价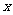 的范围.
的范围.
67.(2009年新疆)解方程: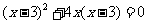 .
.
[关键词]解一元二次方程
[答案]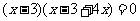 ,
,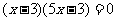 ,
,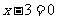 或
或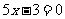 ,
,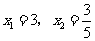
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com