
12、(2009年天津市)已知函数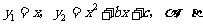 为方程
为方程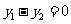 的两个根,点
的两个根,点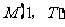 在函数
在函数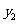 的图象上.
的图象上.
(Ⅰ)若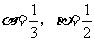 ,求函数
,求函数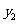 的解析式;
的解析式;
(Ⅱ)在(Ⅰ)的条件下,若函数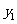 与
与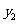 的图象的两个交点为
的图象的两个交点为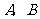 ,当
,当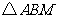 的面积为
的面积为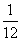 时,求
时,求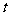 的值;
的值;
(Ⅲ)若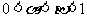 ,当
,当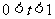 时,试确定
时,试确定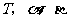 三者之间的大小关系,并说明理由.
三者之间的大小关系,并说明理由.
11、(2009年新疆)(1)用配方法把二次函数 变成
变成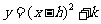 的形成.
的形成.
(2)在直角坐标系中画出 的图象.
的图象.
(3)若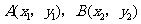 是函数
是函数 图象上的两点,且
图象上的两点,且 ,请比较
,请比较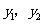 的大小关系.(直接写结果)
的大小关系.(直接写结果)
(4)把方程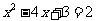 的根在函数
的根在函数 的图象上表示出来.
的图象上表示出来.
[
10、(2009年孝感)已知抛物线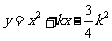 (k为常数,且k>0).
(k为常数,且k>0).
(1)证明:此抛物线与x轴总有两个交点;
(2)设抛物线与x轴交于M、N两点,若这两点到原点的距离分别为OM、ON,且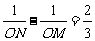 ,求k的值.
,求k的值.
9、(2009烟台市)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
7、(2009年娄底)已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)探究m满足什么条件时,二次函数y的图象与x轴的交点的个数.
(2)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且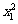 +
+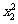 =5,与y轴的交点为C,它的顶点为M,求直线CM的解析式.
=5,与y轴的交点为C,它的顶点为M,求直线CM的解析式.
6、(2009年杭州市)已知平行于x轴的直线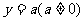 与函数
与函数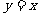 和函数
和函数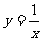 的图象分别交于点A和点B,又有定点P(2,0).
的图象分别交于点A和点B,又有定点P(2,0).
(1)若 ,且tan∠POB=
,且tan∠POB=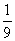 ,求线段AB的长;
,求线段AB的长;
(2)在过A,B两点且顶点在直线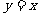 上的抛物线中,已知线段AB=
上的抛物线中,已知线段AB= ,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
,且在它的对称轴左边时,y随着x的增大而增大,试求出满足条件的抛物线的解析式;
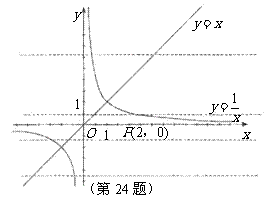
 (3)已知经过A,B,P三点的抛物线,平移后能得到
(3)已知经过A,B,P三点的抛物线,平移后能得到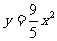 的图象,求点P到直线AB的距离.
的图象,求点P到直线AB的距离.
5、(2009年内蒙古包头)某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量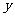 (件)与销售单价
(件)与销售单价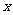 (元)符合一次函数
(元)符合一次函数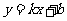 ,且
,且 时,
时, ;
;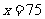 时,
时,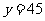 .
.
(1)求一次函数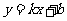 的表达式;
的表达式;
(2)若该商场获得利润为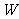 元,试写出利润
元,试写出利润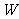 与销售单价
与销售单价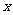 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价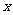 的范围.
的范围.
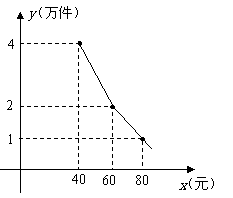
4、(2009年湖南长沙)为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量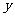 (万件)与销售单价
(万件)与销售单价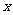 (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求月销售量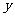 (万件)与销售单价
(万件)与销售单价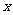 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)当销售单价定为50元时,为保证公司月利润达到5万元(利润=销售额-生产成本-员工工资-其它费用),该公司可安排员工多少人?
(3)若该公司有80名员工,则该公司最早可在几个月后还清无息贷款?

3、(2009年常德市)已知二次函数过点A (0, ),B(
),B( ,0),C(
,0),C(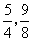 ).
).
(1)求此二次函数的解析式;
(2)判断点M(1, )是否在直线AC上?
)是否在直线AC上?
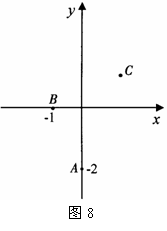 (3)过点M(1,
(3)过点M(1, )作一条直线
)作一条直线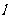 与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
与二次函数的图象交于E、F两点(不同于A,B,C三点),请自已给出E点的坐标,并证明△BEF是直角三角形.
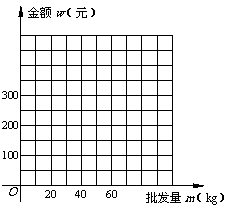
2、(2009 安徽)已知某种水果的批发单价与批发量的函数关系如图(1)所示.
(1)请说明图中①、②两段函数图象的实际意义.
[解]

(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的
函数关系式;在下图的坐标系中画出该函数图象;指出金额在什
么范围内,以同样的资金可以批发到较多数量的该种水果.
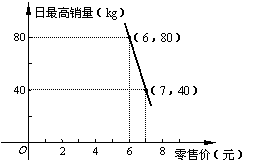
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函
数关系如图(2)所示,该经销商拟每日售出60kg以上该种水果,
且当日零售价不变,请你帮助该经销商设计进货和销售的方案,
使得当日获得的利润最大.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com