
3.(2009年泸州)如图l,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,则∠PBP’的度数是
A.45° B.60°
C.90° D.120°
2. (2009年株洲市)如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四个完全相同的四边形 拼成的.测得
拼成的.测得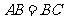 ,
,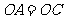 ,
, ,
, ,则
,则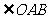 的度数是
的度数是
A. B.
B.
C. D.
D.
1.  (2009年株洲市)下列四个图形中,不是轴对称图形的是
(2009年株洲市)下列四个图形中,不是轴对称图形的是
A. B. C. D.
13. (2009年达州)如图10,⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E,AC∥DE交BD于点H,DO及延长线分别交AC.BC于点G、F.
(1)求证:DF垂直平分AC;
(2)求证:FC=CE;
(3)若弦AD=5㎝,AC=8㎝,求⊙O的半径.
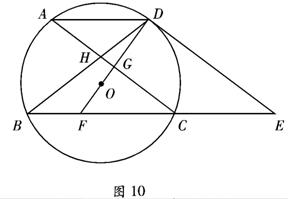
[关键词]圆,平行四边形,勾股定理
[答案]
(1)∵DE是⊙O的切线,且DF过圆心O
∴DF⊥DE
又∵AC∥DE
∴DF⊥AC
∴DF垂直平分AC
(2)由(1)知:AG=GC
又∵AD∥BC
∴∠DAG=∠FCG
又∵∠AGD=∠CGF
∴△AGD≌△CGF(ASA)
∴AD=FC
∵AD∥BC且AC∥DE
∴四边形ACED是平行四边形
∴AD=CE
∴FC=CE5分
(3)连结AO; ∵AG=GC,AC=8cm,∴AG=4cm
在Rt△AGD中,由勾股定理得 GD=AD2-AG2=52-42=3cm
设圆的半径为r,则AO=r,OG=r-3
在Rt△AOG中,由勾股定理得 AO2=OG2+AG2
有:r2=(r-3)2+42解得 r=256
∴⊙O的半径为256cm.
12.(2009年山东青岛市)如图,在梯形ABCD中, ,
,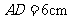 ,
, ,
,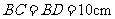 ,点
,点 由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交
由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交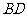 于Q,连接PE.若设运动时间为
于Q,连接PE.若设运动时间为 (s)(
(s)( ).解答下列问题:
).解答下列问题:
(1)当 为何值时,
为何值时,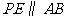 ?
?
(2)设 的面积为
的面积为 (cm2),求
(cm2),求 与
与 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻 ,使
,使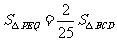 ?若存在,求出此时
?若存在,求出此时 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(4)连接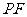 ,在上述运动过程中,五边形
,在上述运动过程中,五边形 的面积是否发生变化?说明理由.
的面积是否发生变化?说明理由.


[关键词]全等三角形的性质与判定、相似三角形判定和性质、平行四边形有关的计算
[答案]


解:(1)∵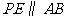
∴ .
.
而 ,
,
∴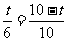 ,
,
∴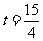 .
.
∴当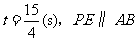 .
.
(2)∵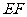 平行且等于
平行且等于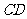 ,
,
∴四边形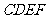 是平行四边形.
是平行四边形.
∴ .
.
∵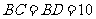 ,
,
∴ .
.
∴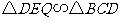 .
.
∴ .
.
 .
.
∴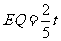 .
.
过B作 ,交
,交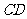 于
于 ,过
,过 作
作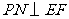 ,交
,交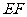 于
于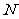 .
.
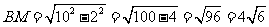 .
.
∵ ,
,
∴ .
.
又 ,
,
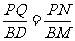 ,
,
 ,
,

 .
.
(3)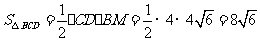 .
.
若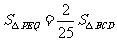 ,
,
则有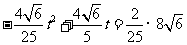 ,
,
解得 .
.
(4)在 和
和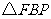 中,
中,
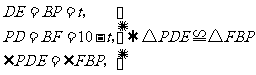
∴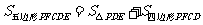

 .
.
∴在运动过程中,五边形 的面积不变.
的面积不变.
11.(2009年宁德市)(本题满分8分)如图:点A.D.B.E在同一直线上,AD=BE,AC=DF,AC∥DF,请从图中找出一个与∠E相等的角,并加以证明.(不再添加其他的字母与线段)


[关键词]平行四边形的判定
[答案]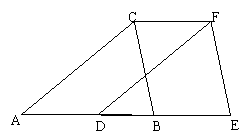 解法1:图中∠CBA=∠E
解法1:图中∠CBA=∠E
证明:∵AD=BE
∴AD+DB=BE+DB即AB=DE
∵AC∥DF ∴∠A=∠FDE
又∵AC=DF
∴△ABC≌△DEF
∴∠CBA=∠E


解法2:图中∠FCB=∠E
证明:∵AC=DF,AC∥DF
∴四边形ADFC是平行四边形
∴CF∥AD,CF=AD
∵AD=BE ∴CF=BE,CF∥BE
∴四边形BEFC是平行四边形
∴∠FCB=∠E
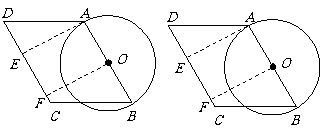
10.(2009年中山)在 中,
中,
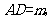
 ,
,
以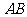 为直径作
为直径作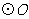 ,
,
(1)求圆心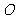 到
到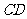 的距离(用含
的距离(用含 的代数式来表示);
的代数式来表示);
(2)当 取何值时,
取何值时,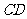 与
与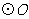 相切.
相切.


[关键词]利用平行四边形证明线段相等
[答案](1)分别过 两点作
两点作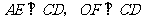 ,垂足分别为点
,垂足分别为点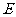 ,点
,点 ,
,
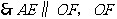 就是圆心
就是圆心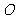 到
到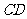 的距离.
的距离.
 四边形
四边形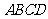 是平行四边形,
是平行四边形,
 .
.

在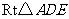 中,
中, ,
,
 ,
,
圆心到CD的距离PF为 .
.
(2)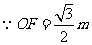 ,
,
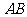 为
为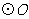 的直径,且
的直径,且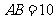 ,
,
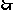 当
当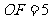 时,
时,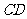 与
与 相切于
相切于 点,
点,
即 ,
,
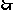 当
当 时,
时, 与
与 相切.
相切.
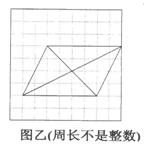
9.(2009年温州)在所给的9×9方格中,每个小正方形的边长都是1.按要求画平行四边形,使它的四个顶点以及对角线交点都在方格的顶点上.
(1)在图甲中画一个平行四边形,使它的周长是整数;(2)在图乙中画一个平行四边形,使它的周长不是整数.(注:图甲、图乙在答题纸上)
[关键词]平行四边形的性质,判定
[答案]解:(1)


(2)

8.(2009年莆田)已知:如图在 中,过对角线
中,过对角线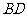 的中点
的中点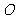 作直线
作直线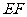 分别交
分别交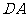 的延长线、AB、DC、BC的延长线于点E、M、N、F。
的延长线、AB、DC、BC的延长线于点E、M、N、F。
(1)观察图形并找出一对全等三角形: ________
________
 ____________,请加以证明;
____________,请加以证明;
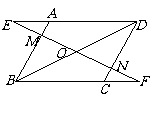



(2)在(1)中你所找出的一对全等三角形,其中一个三角形可由另一个三角形经过怎样的变换得到?
[关键词]四边形、全等三角形、变换
(1)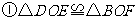 ;
;
证明:∵四边形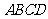 是平行四边形
∴
是平行四边形
∴
∴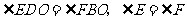
又∵
∴
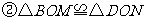
证明:∵四边形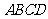 是平行四边形
∴
是平行四边形
∴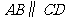
∴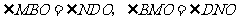
又∵
∴
 ;
;
证明:∵四边形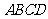 是平行四边形
∴
是平行四边形
∴
又∵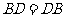
∴
(2)绕点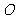 旋转
旋转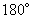 后得到或以点
后得到或以点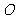 为中心作对称变换得到. 8分
为中心作对称变换得到. 8分
7.(2009年包头)已知二次函数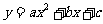 (
( )的图象经过点
)的图象经过点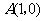 ,
, ,
,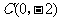 ,直线
,直线 (
(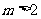 )与
)与 轴交于点
轴交于点 .
.
(1)求二次函数的解析式;
(2)在直线 (
(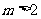 )上有一点
)上有一点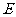 (点
(点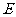 在第四象限),使得
在第四象限),使得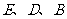 为顶点的三角形与以
为顶点的三角形与以 为顶点的三角形相似,求
为顶点的三角形相似,求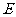 点坐标(用含
点坐标(用含 的代数式表示);
的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点 ,使得四边形
,使得四边形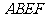 为平行四边形?若存在,请求出
为平行四边形?若存在,请求出 的值及四边形
的值及四边形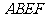 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.


[关键词]二次函数、相似三角形、运动变化、抛物线
解:(1)根据题意,得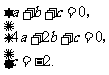
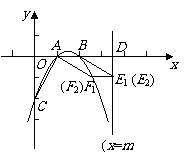

解得 .
.
 .
.
(2)当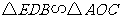 时,
时,
得 或
或 ,
,
∵ ,
,
当 时,得
时,得 ,
,
∴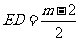 ,
,
∵点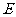 在第四象限,∴
在第四象限,∴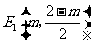 .
.
当 时,得
时,得 ,∴
,∴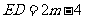 ,
,
∵点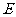 在第四象限,∴
在第四象限,∴ .
.
(3)假设抛物线上存在一点 ,使得四边形
,使得四边形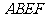 为平行四边形,则
为平行四边形,则
 ,点
,点 的横坐标为
的横坐标为 ,
,
当点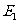 的坐标为
的坐标为 时,点
时,点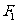 的坐标为
的坐标为 ,
,
∵点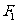 在抛物线的图象上,
在抛物线的图象上,
∴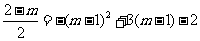 ,
,
∴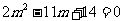 ,
,
∴ ,
,
∴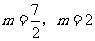 (舍去),
(舍去),
∴ ,
,
∴ .
.
当点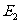 的坐标为
的坐标为 时,点
时,点 的坐标为
的坐标为 ,
,
∵点 在抛物线的图象上,
在抛物线的图象上,
∴ ,
,
∴ ,
,
∴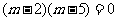 ,∴
,∴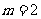 (舍去),
(舍去),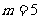 ,
,
∴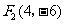 ,
,
∴ .
.
注:各题的其它解法或证法可参照该评分标准给分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com