
3、(2009年重庆)如图,直线 相交于点
相交于点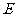 ,
, .若
.若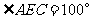 ,
,
则 等于( )
等于( )
A.70° B.80° C.90° D.100°

2、(2009年福州)已知∠1=30°,则∠1的余角度数是( )
A.160° B.150° C.70° D.60°
1、(2009年日照)如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于
A .70° B .65° C .50° D .25°

7.(2009年安徽)19.学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示.已知每个菱形图案的边长 cm,其一个内角为60°.
cm,其一个内角为60°.

(1)若d=26,则该纹饰要231个菱形图案,求纹饰的长度L;
(2)当d=20时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?
[答案](1)6010 cm(2)需300个这样的菱形图案.
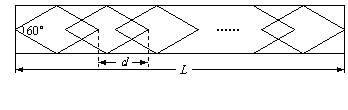
6.(2009年衢州)如图,AD是⊙O的直径.
(1) 如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是 ,∠B2的度数是 ;
(2) 如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,
∠B3的度数;
(3) 如图③,垂直于AD的n条弦B1C1,B2C2,B3 C3,…,BnCn把圆周2n等分,请你用含n的代数式表示∠Bn的度数(只需直接写出答案).

[答案]解:(1) 22.5°,67.5°
(2) 45°, 75°.
(3) 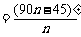 .(或
.(或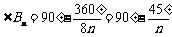 )
)
5.(2009白银市)29.本试卷第19题为:若 ,
,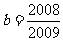 ,试不用将分数化小数的方法比较a、b的大小.
,试不用将分数化小数的方法比较a、b的大小.
观察本题中数a、b的特征,以及你比较大小的过程,直接写出你发现的一个一般结论.
[答案]29.解:学生可能写出不同程度的一般的结论,由一般化程度不同得不同分.
若m、n是任意正整数,且m>n,则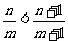 .
.
若m、n是任意正实数,且m>n,则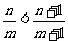 .
.
若m、n、r是任意正整数,且m>n;或m、n是任意正整数,r是任意正实数,且m>n,则 .
.
若m、n是任意正实数,r是任意正整数,且m>n;或m、n、r是任意正实数,且m>n,则 .
.
4.(2009恩施市) 宽与长之比为
宽与长之比为 ∶
∶ 的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图9,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
的矩形叫黄金矩形,黄金矩形令人赏心悦目,它给我们以协调,匀称的美感,如图9,如果在一个黄金矩形里画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.
[答案]解: 留下的矩形CDFE是黄金矩形 。
3.(2009年杭州市)如图,在等腰梯形ABCD中,∠C=60°,AD∥BC,且AD=DC,E、F分别在AD、DC的延长线上,且DE=CF,AF、BE交于点P.
(1)求证:AF=BE;
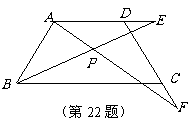 (2)请你猜测∠BPF的度数,并证明你的结论.
(2)请你猜测∠BPF的度数,并证明你的结论.
[答案](1)BE=AF;
(2)猜想∠BPF=120° .
2.(2009年台州市)将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则
①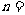 ;②第
;②第 行第
行第 列的数为 (用
列的数为 (用 ,
, 表示).
表示).
|
|
第 列 列 |
第 列 列 |
第 列 列 |
… |
第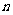 列 列 |
第 行 行 |
1 |
 |
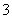 |
… |
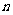 |
第 行 行 |
 |
 |
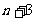 |
… |
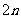 |
第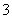 行 行 |
 |
 |
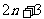 |
… |
 |
|
… |
… |
… |
… |
… |
… |
[答案]10,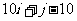 (第一空2分,第二空3分;答
(第一空2分,第二空3分;答 给3分,答
给3分,答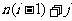 给2分)
给2分)
1.(2009仙桃)如图所示,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,如图①,然后将△ADE绕A点顺时针旋转一定角度,得到图②,然后将BD、CE分别延长至M、N,使DM= BD,EN=
BD,EN= CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:
(1)若AB=AC,请探究下列数量关系:
①在图②中,BD与CE的数量关系是________________;
②在图③中,猜想AM与AN的数量关系、∠MAN与∠BAC的数量关系,并证明你的猜想;
(2)若AB=k·AC(k>1),按上述操作方法,得到图④,请继续探究:AM与AN的数量关系、∠MAN与∠BAC的数量关系,直接写出你的猜想,不必证明.
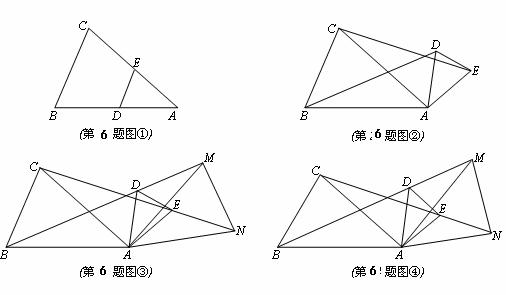
[答案]解:(1)①BD=CE;②AM=AN,∠MAN=∠BAC.
(2)AM= AN,∠MAN=∠BAC.
AN,∠MAN=∠BAC.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com