
2.解决匀速圆周运动问题的一般方法
(1)明确研究对象,必要时将它从转动系统中隔离出来。
(2)找出物体圆周运动的轨道平面,从中找出圆心和半径。
(3)分析物体受力情况,千万别臆想出一个向心力来。
(4)建立直角坐标系(以指向圆心方向为x轴正方向)将力正交分解。
(5)
5.竖直平面内的圆周运动
竖直平面内的圆周运动是典型的变速圆周运动研究物体通过最高点和最低点的情况,并且经常出现临界状态。(圆周运动实例)
①火车转弯
②汽车过拱桥、凹桥3
③飞机做俯冲运动时,飞行员对座位的压力。
④物体在水平面内的圆周运动(汽车在水平公路转弯,水平转盘上的物体,绳拴着的物体在光滑水平面上绕绳的一端旋转)和物体在竖直平面内的圆周运动(翻滚过山车、水流星、杂技节目中的飞车走壁等)。
⑤万有引力--卫星的运动、库仑力--电子绕核旋转、洛仑兹力--带电粒子在匀强磁场中的偏转、重力与弹力的合力--锥摆、(关健要搞清楚向心力怎样提供的)
(1)火车转弯:设火车弯道处内外轨高度差为h,内外轨间距L,转弯半径R。由于外轨略高于内轨,使得火车所受重力和支持力的合力F合提供向心力。
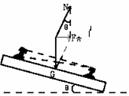

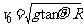 (是内外轨对火车都无摩擦力的临界条件)
(是内外轨对火车都无摩擦力的临界条件)
①当火车行驶速率V等于V0时,F合=F向,内外轨道对轮缘都没有侧压力
②当火车行驶V大于V0时,F合<F向,外轨道对轮缘有侧压力,F合+N=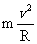
③当火车行驶速率V小于V0时,F合>F向,内轨道对轮缘有侧压力,F合-N'=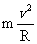
即当火车转弯时行驶速率不等于V0时,其向心力的变化可由内外轨道对轮缘侧压力自行调节,但调节程度不宜过大,以免损坏轨道。
(2)无支承的小球,在竖直平面内作圆周运动过最高点情况:
①
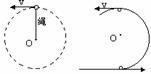 临界条件:由mg+T=mv2/L知,小球速度越小,绳拉力或环压力T越小,但T的最小值只能为零,此时小球以重力提供作向心力,恰能通过最高点。即mg=
临界条件:由mg+T=mv2/L知,小球速度越小,绳拉力或环压力T越小,但T的最小值只能为零,此时小球以重力提供作向心力,恰能通过最高点。即mg=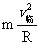
结论:绳子和轨道对小球没有力的作用(可理解为恰好通过或恰好通不过的速度),只有重力提供作向心力,临界速度V临=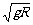
②能过最高点条件:V≥V临(当V≥V临时,绳、轨道对球分别产生拉力、压力)
③不能过最高点条件:V<V临(实际上球还未到最高点就脱离了轨道)
最高点状态: mg+T1=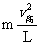 (临界条件T1=0, 临界速度V临=
(临界条件T1=0, 临界速度V临=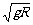 , V≥V临才能通过)
, V≥V临才能通过)
最低点状态: T2- mg = 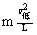
高到低过程机械能守恒: 
T2- T1=6mg(g可看为等效加速度)
半圆:mgR=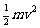 T-mg=
T-mg=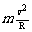
 T=3mg
T=3mg
(3)有支承的小球,在竖直平面作圆周运动过最高点情况:
①临界条件:杆和环对小球有支持力的作用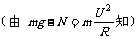 当V=0时,N=mg(可理解为小球恰好转过或恰好转不过最高点)
当V=0时,N=mg(可理解为小球恰好转过或恰好转不过最高点)
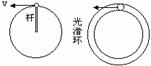


恰好过最高点时,此时从高到低过程 mg2R=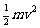 低点:T-mg=mv2/R
低点:T-mg=mv2/R
 T=5mg
T=5mg
注意物理圆与几何圆的最高点、最低点的区别 (以上规律适用于物理圆,不过最高点,最低点, g都应看成等效的)
4.平抛运动:匀速直线运动和初速度为零的匀加速直线运动的合运动
(1)运动特点:a、只受重力;b、初速度与重力垂直.尽管其速度大小和方向时刻在改变,但其运动的加速度却恒为重力加速度g,因而平抛运动是一个匀变速曲线运动。在任意相等时间内速度变化相等。
(2)平抛运动的处理方法:平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动。
水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.
(3)平抛运动的规律:以物体的出发点为原点,沿水平和竖直方向建成立坐标。
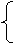
 ax=0……①
ay=0……④
ax=0……①
ay=0……④
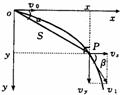 水平方向 vx=v0 ……② 竖直方向 vy=gt……⑤
水平方向 vx=v0 ……② 竖直方向 vy=gt……⑤
x=v0t……③ y=½gt2……⑥
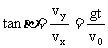 Vy
= Votgq Vo
=Vyctgβ
Vy
= Votgq Vo
=Vyctgβ
V = 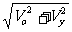 Vo = Vcosq Vy
= Vsinβ
Vo = Vcosq Vy
= Vsinβ
在Vo、Vy、V、X、y、t、q七个物理量中,如果 已知其中任意两个,可根据以上公式求出其它五个物理量。
证明:做平抛运动的物体,任意时刻速度的反向延长线一定经过此时沿抛出方向水平总位移的中点。
证:平抛运动示意如图
设初速度为V0,某时刻运动到A点,位置坐标为(x,y ),所用时间为t.
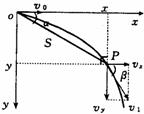 此时速度与水平方向的夹角为
此时速度与水平方向的夹角为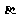 ,速度的反向延长线与水平轴的交点为
,速度的反向延长线与水平轴的交点为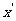 ,
,
位移与水平方向夹角为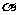 .依平抛规律有:
.依平抛规律有:
速度: Vx= V0
Vy=gt

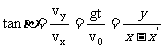 ①
①
位移: Sx= Vot 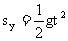
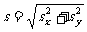
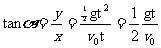 ②
②
由①②得: 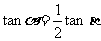 即
即 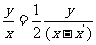 ③
③
所以: 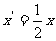 ④
④
④式说明:做平抛运动的物体,任意时刻速度的反向延长线一定经过此时沿抛出方向水总位移的中点。
3.匀速圆周运动
线速度: V=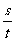 =
=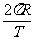 =wR=2
=wR=2 f R
角速度:w=
f R
角速度:w=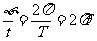 追及问题:wAtA=wBtB+n2π
追及问题:wAtA=wBtB+n2π
向心加速度: a =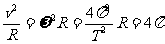 2 f2
R
2 f2
R
向心力: F= ma = m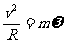 2 R= m
2 R= m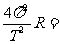 m4
m4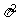 n2 R
n2 R
注意:(1)匀速圆周运动的物体的向心力就是物体所受的合外力,总是指向圆心.
(2)卫星绕地球、行星绕太阳作匀速圆周运动的向心力由万有引力提供。
(3)氢原子核外电子绕原子核作匀速圆周运动的向心力由原子核对核外电子的库仑力提供。
2.竖直上抛运动:(速度和时间的对称)
分过程:上升过程匀减速直线运动,下落过程初速为0的匀加速直线运动.
全过程:是初速度为V0加速度为-g的匀减速直线运动。
(1)上升最大高度:H = 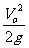
(2)上升的时间:t= 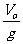
(3)上升、下落经过同一位置时的加速度相同,而速度等值反向
(4)上升、下落经过同一段位移的时间相等。
(5)从抛出到落回原位置的时间:t =2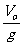
(6)适用全过程S = Vo t - g t2 ;
Vt = Vo-g t ; Vt2-Vo2 = -2gS (S、Vt的正、负号的理解)
g t2 ;
Vt = Vo-g t ; Vt2-Vo2 = -2gS (S、Vt的正、负号的理解)
8.巧用匀变速直线运动的推论解题
①某段时间内的平均速度 = 这段时间中时刻的即时速度
②连续相等时间间隔内的位移差为一个恒量
③位移=平均速度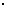 时间
时间
解题常规方法:公式法(包括数学推导)、图象法、比例法、极值法、逆向转变法
7.用比例法解题
6.应用运动学图象解题
5.逆向思维法解题
4.利用运动的对称性解题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com