5．下列各句，没有语病的一项是　　　　　　　　　　　　　　　　　　　　 (　　 )

A．奥运会后各主办城市的经济状况与奥运会市场化运作程度、全球经济形势、各主办国经济发展阶段以及产业结构特点等因素密切相关。

B．生产性消费在我国消费结构中占有比发达国家明显重要得多的地位，这些年来积累率占GDP的比重一般比发达国家要高出至少15%以上。

C．国学热的出现在一定意义上是对当前值得堪忧的社会人文环境的一种回应，在很大程度上，社会人文环境的恶劣直接导致人们渴望去寻求一种精神归属。

D．优秀近现代建筑的保护现状不尽如人意，其主要原因是缺乏有效的法律、法规和手段对近现代建筑进行保护和管理造成的。

4．下列各句，没有语病的一项是　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．为帮助绵竹灾区中小学尽快恢复正常的教育教学秩序，江苏教育部门派出了第一批支教团由来自南京、无锡、徐州、扬州等9个市、县(市、区)的58名中小学教师组成。

B．在社会竞争和生活压力不断增大的今天，将大众化的文艺作品仅仅看作学习、工作之余的消遣、休闲，通过娱乐来获得休息，逐渐成为一种主流的生活方式。

C．纵观我国的这些奥运题材电影，它们都在努力向公众传达努力拼搏、重在参与、超越自我的体育精神以及中华民族的奥运梦想。

D．《加油，中国》运用大量珍贵的影像资料、图片资料和历史资料，以文献片的形式回顾了我国竞技体育不断突破的骄人成绩，展现了中国的百年奥运史和体育发展史。

3．下列各句，没有语病的一项是　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．影片的震撼力来自它深邃的立意、厚重的内涵、完美无缺的人物刻画和精到完整的舞台结构，来自它为人物所构设的悲剧命运的不可逆转性，这些共同构建了它的美学品位。

B．宋代著名文学家、历史学家、政治家欧阳修在滁州任知州期间，写下了流传千古的散文名篇《醉翁亭记》，至今，关于欧阳修和他的《醉翁亭记》的报道还屡屡见诸于报端。

C．《立秋》是用传统创作方法反映地方文化的戏剧，它所蕴含的很深刻的一个意义就是要提醒现代人，我们的华夏五千年文明是令人骄傲的，它的文化积淀广博而深厚，

D．中国传统文化的“悲秋”情结延续了几千年，秋之肃杀与人之断肠总是紧紧地连接在一起。而艺术作品，要有一个可以“组成本质的个别标志”来作为寄寓主题、情感。

2．下列各句，没有语病的一项是　　　　　　　　　　　　　　　　　　　　　 (　　 )

A．在高温下，成熟的香蕉放不过3天，而从去年每斤1元五角钱的收购价到现在每斤一角钱，价格暴跌10倍却依然无人问津，使蕉农苦不堪言。

B．如何使青少年既懂得保持本民族价值规范体系，又能汲取世界优秀文化营养，既有国际眼光、世界意识，又有民族自信心、自尊心，这是一个极其重要的教育课题。

C．商品零售场所必须对塑料购物袋明码标价，并在商品价外收取塑料购物袋价款。这让很多消费者担心，自己负担的环保成本，会不会成为商家创收的一个来源。

D．大师所代表的不仅仅是学术、思想或文艺等某一领域的辉煌，更重要的是，他以广博的学识、深刻的心灵和不朽的经典向人们展示了什么才是真正的伟大作品。

1．下列各句，不是“成分残缺”语病的一项是　　　　　　　　　　　　　　　 (　　 )

　　 A．话题作文给当时限制过死、封闭的作文教学以振聋发聩的一击，它对激发学生的想象和联想，推动作文教学的改革，起了一定的积极作用。

　　 B．我国的经济发展正面临越来越大的资源、环境压力，高消耗、高污染、粗放式经济增长方式尚未扭转。

C．以建设社会治安综合治理先进省为载体，从建设平安市县区着手，使社会治安明显改善，防止发生重特大刑事案件。

D．明年在基本完成城市集中连片5万平方米以上棚户区的改造任务基础上，着手探索改造分散的棚户区。

2．已知直线l₁：mx－y＝0，l₂：x+my－m－2＝0.

　 (1)求证：对m的任意实数值，l₁和l₂的交点P在一定圆上；

　 (2)若l₁与定圆另一交点P₁，l₂与定圆另一交点为P₂，求当m在实数范围内取值时，△PP₁P₂的面积的最大值，并求此时l₁的方程．

　 解答：(1)证明：由mx－y＝0，得m＝代入x+my－m－2＝0中得x+y－－2＝0，即x²+y²－y－2x＝0，亦即(x－1)²+(y－)²＝，所以，l₁和l₂的交点在定圆上．

　 (2)由消去y，得(1+m²)x²－(m+2)x＝0，

　 ∴P₁(0,0)，P(，)．∴|P₁P|＝ ＝.

　 由

　 得P₂(2,1)，∵|P₂P|＝ ＝，

　 又∵l₁⊥l₂，∴△PP₁P₂为直角三角形．

　 ∴S△PP₁P₂＝|P₁P|·|P₂P|＝·＝·.

　 令y＝，则(y－2)m²－3m+y+2＝0.①

　 当y≠2时，应有Δ＝(－3)²－4(y－2)(y+2)≥0.得－≤y≤，

　 ∴||的最大值为，∴△PP₁P₂的最大面积为，

　 此时y＝±代入①式中求得m＝3或－.

　 ∴此时l₁的方程为y＝3x或y＝－x.

1．一直线经过点P(－3，－)被圆x²+y²＝25截得的弦长为8，求此弦所在直线方程．

　 解答： (1)当斜率k不存在时，过点P的直线方程为x＝－3，代入x²+y²＝25，得y₁＝4，y₂＝－4.

　 ∴弦长为|y₁－y₂|＝8，符合题意．

　 (2)当斜率k存在时，设所求直线方程为y+＝k(x+3)，即kx－y+3k－＝0.

　 由已知，弦心距|OM|＝ ＝3，∴＝3，解得k＝－.

　 所以此直线方程为y+＝－(x+3)，即3x+4y+15＝0.

　 所以所求直线方程为x+3＝0或3x+4y+15＝0.

10．如右图所示，已知圆C₁：x²+y²－2mx－2ny+m²－1＝0和圆

　 　C₂：x²+y²+2x+2y－2＝0交于

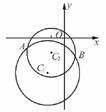
　 A、B两点且这两点平分圆C₂的圆周．求圆C₁的圆心C₁的轨迹方程，并求出当圆C₁的半径最小时圆C₁的方程．

　 解答：圆C₁：(x－m)²+(y－n)²＝n²+1，圆C₂：(x+1)²+(y+1)²＝4，而C₁C₂⊥AB且AB为圆C₂直径．

　 ∴|AC₂|＝rc₂＝2，又|AC₁|²＝rc₁²＝1+n²，|AC₂|²＝4，|C₁C₂|²＝(m+1)²+(n+1)².

　 在Rt△AC₂C₁中，由勾股定理，得4+(m+1)²+(n+1)²＝1+n²，∴(m+1)²＝－2(n+2)即为点C₁的轨迹方程．

　 又－2(n+2)≥0，n≤－2，当n＝－2时，m＝－1，

　 rc₁min＝，此时圆C₁的方程为(x+1)²+(y+2)²＝5.

★选做题

9．如右图，已知直角坐标平面上点Q(2,0)和圆C：x²+y²＝1，动点M到圆C的切线长与|MQ|的比等于常数λ(λ>0)．

　 求动点M的轨迹方程，说明它表示什么曲线．

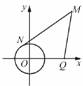
　 解答：如右图，设M(x，y)，MN切圆于N，则＝λ，即|MN|＝λ|MQ|.又|MN|²＝|MO|²－1＝x²+y²－1，∴|MN|＝，又|MQ|＝，∴＝λ整理得　(λ²－1)(x²+y²)－4λ²x+(1+4λ²)＝0，即为所求的轨迹方程．当λ＝1时，方程化为x＝，表示一条直线；当λ≠1时，方程化为(x－)²+y²＝，它表示圆，圆心为(，0)，半径为.

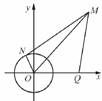
8．过圆x²+y²＝r²(r＞0)外一点P(x₀，y₀)作圆的两条切线，切点分别为M、N，证明直线MN的方程是x₀x+y₀y＝r².

　 证明：证法一：设M、N的坐标分别为(x₁，y₁)、(x₂，y₂)．∵M、N在圆x²+y²＝r²上，

　 ∴过M、N的切线方程分别是：x₁x+y₁y＝r²，x₂x+y₂y＝r²，又P是两切线公共点，即有：x₁x₀+y₁y₀＝r²，x₂x₀+y₂y₀＝r²，上两式表明点M(x₁，y₁)，N(x₂，y₂)都在二元一次方程x₀x+y₀y＝r²表示的直线上．所以直线MN的方程是x₀x+y₀y＝r².

　 证法二：以OP为直径的圆的方程为：(x－x₀)²+(y－y₀)²＝(x+y)，即x²+y²－x₀x－y₀y＝0，又圆的方程是x²+y²＝r²，两式相减得x₀x+y₀y＝r²，这便是过切点M、N的直线方程．