
4. (2006山东)已知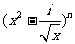 的展开式中第三项与第五项的系数之比为
的展开式中第三项与第五项的系数之比为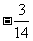 ,其中
,其中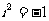 ,则展开式中常数项是
( )
,则展开式中常数项是
( )
A.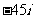 B.
B.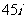 C.
C.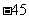 D.
D.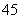
3.在复平面内,若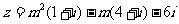 所对应的点在第二象限,则实数m的取值范围是
( )
所对应的点在第二象限,则实数m的取值范围是
( )
A.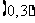 B.
B. C.
C.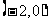 D.
D.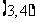
2.(2006浙江)已知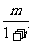 =1-ni,其中m,n是实数,i是虚数单位,则m+ni= ( )
=1-ni,其中m,n是实数,i是虚数单位,则m+ni= ( )
(A) (B)
(B) 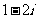 (C)
(C)
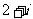 (D)
(D)
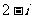
1.(2006全国Ⅰ)如果复数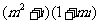 是实数,则实数
是实数,则实数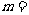 ( )
( )
A. 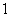 B.
B. 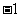 C .
C .  D.
D. 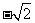
8.由复数相等的定义知:实系数一元二次方程ax2+bx+c=0在当Δ<0时,有一对共轭虚根.
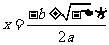
7.掌握复数的和、差、积、商运算法则:
z1±z2=(a+bi) ±(c+di)=(a±c)+(b±d)i; (a+bi)(c+di)=(ac-bd)+(bc+ad)i;
(a+bi)÷(c+di)=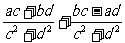 i(即分子分母同乘以分母的共轭复数,再化简).
i(即分子分母同乘以分母的共轭复数,再化简).
复数运算满足加、乘的交换律、结合律、分配律.
6.复平面、实轴、虚轴:--
复数z=a+bi(a、b∈R)可用点Z(a,b)表示,,虚轴上的点,除原点外,都表示纯虚数.
和向量一样,复数也可用有向线段表示,复数的加减法运算也可按平行四边形法则或三角形法则进行.
5.共轭复数:实部相等,虚部互为相反数:a+bi和a–bi(a,b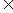 R);
R);
Z的共轭复数用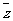 表示,特别地:
表示,特别地: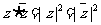
4. 复数的模: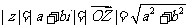 .
.
两个复数不能比较大小,但它们的模可以比较大小;
3.复数相等:设a,b,c,d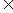 R,则a+bi=c+di
R,则a+bi=c+di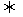 a=c,b=d;a+bi=0
a=c,b=d;a+bi=0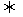 a=b=0;
a=b=0;
利用复数相等的条件转化为实数问题是解决复数问题的常用方法;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com