4．若实数x，y满足等式，那么的最大值是(　)

　A．　　B．　　 C．　　　D．

3．如果函数(a＞0，)是增函数，那么函数的图像大致是(　)

2． 要从其中有50个红球的1000个球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为(　)

　A．5个　　 B．10个　　C．20个　　D．45个

1．设全集U＝R，，，那么下列关系中正确的是(　)

　A．M＝N　　 B．　C．　 D．

15．(1)设装置由静止释放到导体棒运动到磁场下边界的过程中，作用在线框上的安培力做功为W

　　　 由动能定理　

且

解得　

(2)设线框刚离开磁场下边界时的速度为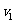，则接着向下运动

由动能定理　

装置在磁场中运动时收到的合力

感应电动势　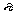 =Bd

感应电流　　 =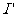

安培力　　　

由牛顿第二定律，在t到t+时间内，有

则

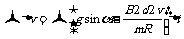
有

解得　

(3)经过足够长时间后，线框在磁场下边界与最大距离之间往复运动

　　 由动能定理　

　　 解得　　

例17 在如图11－24所示的水平导轨上(摩擦、电阻忽略不计)，有竖直向下的匀强磁场，磁感强度B，导轨左端的间距为L₁=4L₀，右端间距为L₂=L₀。今在导轨上放置AC，DE两根导体棒，质量分别为m₁=2m₀，m₂=m₀，电阻R₁=4R₀，R₂=R₀。若AC棒以初速度V₀向右运动，求AC棒运动的过程中产生的总焦耳热Q_AC，以及通过它们的总电量q。

　[错解分析]错解：AC棒在磁场力的作用下，做变速运动。运动过程复杂，应从功能关系的角度来分析。由于没有摩擦，最后稳定的状态应为两棒做匀速运动。根据动量守恒定律m₁v₀=(m₁+m₂)v′

　整个回路产生的焦耳热

　因为R₁=4R₀，R₂=R₀。所以AC棒在运动过程中产生的焦耳热

　对AC棒应用动量定理：BIL₁·△t=m₁v′－m₁v₀

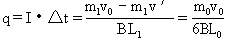
　AC棒在磁场力的作用下做变速运动，最后达到运动稳定，两棒都做匀速运动的分析是正确的。但是以此类推认为两棒的运动速度相同是错误的。如果两棒的速度相同则回路中还有磁通量的变化，还会存在感应电动势，感应电流还会受到安培力的作用，AC，DE不可能做匀速运动。

　[正确解答]

　由于棒L₁向右运动，回路中产生电流，L_l受安培力的作用后减速，L₂受安培力加速使回路中的电流逐渐减小。只需v₁，v₂满足一定关系，

　两棒做匀速运动。

　两棒匀速运动时，I=0，即回路的总电动势为零。所以有

BL_lv₁=BL₂v₂

　再对DE棒应用动量定理BL₂I·△t = m₂v₂

　[小结]

　以前我们做过类似的题。那道题中的平行轨道间距都是一样的。有一些同学不假思索，把那道题的结论照搬到本题中来，犯了生搬硬套的错误。差异就是矛盾。两道题的差别就在平行导轨的宽度不一样上。如何分析它们之间的差别呢？还是要从基本原理出发。平行轨道间距一样的情况两根导体棒的速度相等，才能使回路中的磁通量的变化为零。本题中如果两根导轨的速度一样，由于平行导轨的宽度不同导致磁通量的变化不为零，仍然会有感应电流产生，两根导体棒还会受到安培力的作用，其中的一根继续减速，另一根继续加速，直到回路中的磁通量的变化为零，才使得两根导体棒做匀速运动。抓住了两道题的差异之所在，问题就会迎刃而解。

　例18 如图 11－25所示光滑平行金属轨道abcd，轨道的水平部分bcd处于竖直向上的匀强磁场中，bc部分平行导轨宽度是cd部分的2倍，轨道足够长。将质量相同的金属棒P和Q分别置于轨道的ab段和cd段。P棒位于距水平轨道高为h的地方，放开P棒，使其自由下滑，求P棒和Q棒的最终速度。

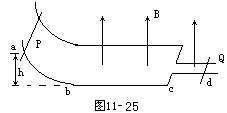
　[错解分析]错解：

　设P，Q棒的质量为m，长度分别为2L和L，磁感强度为B，P棒进入水平轨道的速度为v₀，对于P棒，运用机械能守恒定律得

　当P棒进入水平轨道后，切割磁感线产生感应电流。P棒受到安培力作用而减速，Q棒受到安培力而加速，Q棒运动后也将产生感应电动势，与P棒感应电动势反向，因此回路中的电流将减小。最终达到匀速运动时，回路的电流为零，所以

ε_p=ε_Q

即2BLv_p=BLv_Q

2v_p=v_Q

　对于P，Q棒，运用动量守恒定律得到

mv₀=mv_p+mv_Q

　错解中对P，Q的运动过程分析是正确的，但在最后求速度时运用动量守恒定律出现错误。因为当P，Q在水平轨道上运动时，它们所受到的合力并不为零。F_p=2BIL，F_Q=BIL(设I为回路中的电流)，因此P，Q组成的系统动量不守恒。

　[正确解答]

　设P棒从进入水平轨道开始到速度稳定所用的时间为△t，P，Q 对PQ分别应用动量定理得

　[小结]

　运用动量守恒定律和机械能守恒定律之前，要判断题目所给的过程是否满足守恒的条件。动量守恒的条件是：系统所受的合外力为零，或者是在某一方向上所受的合外力为零，则系统在该方向上动量的分量守恒。

15.(16分)如图所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨间距为l、

　　 足够长且电阻忽略不计，导轨平面的倾角为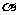，条形匀强磁场的宽度为d，磁感应强度大小为B、方向与导轨平面垂直。长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“”型装置，总质量为m，置于导轨上。导体棒中通以大小恒为I的电流(由外接恒流源产生，图中未图出)。线框的边长为d(d < l)，电阻为R，下边与磁场区域上边界重合。将装置由静止释放，导体棒恰好运动到磁场区域下边界处返回，导体棒在整个运动过程中始终与导轨垂直。重力加速度为g。

求：(1)装置从释放到开始返回的过程中，线框中产生的焦耳热Q；

　 (2)线框第一次穿越磁场区域所需的时间t₁ ；

　 (3)经过足够长时间后，线框上边与磁场区域下边界的最大距离_m 。

14、⑴由动能定理得：

　　　　　　　 解得：

⑵设在最大距离y_m处的速率为v_m，有：

　　　　　 解得：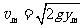

　　　　　　 得：

⑶小球运动如图所示

　　　 由动能定理得：

　　　 由圆周运动得：

　　　　　　　 　且：

　　　　　　　 解得：

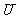在如图所师的闪光灯电路中，电源的电动势为，电容器的电容为。当闪光灯两端电压达到击穿电压时，闪光灯才有电流通过并发光，正常工作时，

　 闪光灯周期性短暂闪光，则可以判定　 D

　　　 A．电源的电动势一定小于击穿电压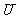　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　 B．电容器所带的最大电荷量一定为

　　　 C．闪光灯闪光时，电容器所带的电荷量一定增大

　　　 D．在一个闪光周期内，通过电阻的电荷量与通过闪光灯的电

　　　　　 荷量一定相等

如图所示，理想变压器的原、副线圈匝数比为1：5，原线圈两端

　 的交变电压为 氖泡在两端电压达到100V

　 时开始发光，下列说法中正确的有 AB

　　　 A．开关接通后，氖泡的发光频率为100Hz

　　　 B．开关接通后，电压表的示数为100 V

　　　 C．开关断开后，电压表的示数变大

　　　 D．开关断开后，变压器的输出功率不变

空间某一静电场的电势在轴上分布如图所示，轴上两点B、C

　 点电场强度在方向上的分量分别是、，下列说法中正确的有AD

　　　 A．的大小大于的大小

　　　 B．的方向沿轴正方向

　　　 C．电荷在点受到的电场力在方向上的分量最大

　　　 D．负电荷沿轴从移到的过程中，电场力先做正功，后做负功

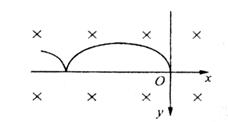
14、(16分)在场强为B的水平匀强磁场中，一质量为m、带正电q的小球在O静止释放，小球的运动曲线如图所示．已知此曲线在最低点的曲率半径为该点到x轴距离的2倍，重力加速度为g．求：

⑴小球运动到任意位置P(x，y)的速率v；

　 ⑵小球在运动过程中第一次下降的最大距离y_m；

⑶当在上述磁场中加一竖直向上场强为E()的匀强电场时，小球从O静止释放后获得的最大速率v_m．

15、⑴a和b不受安培力作用，由机械能守恒得

⑵由能量守恒得：

　 在磁场区域有：

　 在无磁场区域：

　　　　　 解得：

⑶在无磁场区域有：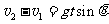

　　　　　 　　且：

　 在有磁场区域，对a棒：

　　　　　　　 且：

　　　　　　 则有：

　　　　　　 解得：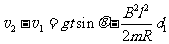

在如图所示的逻辑电路中，当A端输入电信号“1”、B端输入电信号“0”时，则在C和D端输出的电信号分别为(C)

　A．1和0　　 　B．0和1　　

　C．1和l　　　 　D．0和0

如图所示的电路中，三个相同的灯泡a、b、c和电感L₁、L₂与直流电源连接，电感的电阻忽略不计．电键K从闭合状态突然断开时，下列判断正确的有AD　

　 　A．a先变亮，然后逐渐变暗

B．b先变亮，然后逐渐变暗

C．c先变亮，然后逐渐变暗

D．b、c都逐渐变暗

17．(14分)

⑴ 从A点射出的粒子，由A到A′的运动时间为T，根据运动轨迹和对称性可得

　 　　　x轴方向　 　　　　　　(1分)

　 　　y轴方向 　　(1分)

　 　　得：　 (2分)

⑵ 设到C点距离为△y处射出的粒子通过电场后也沿x轴正方向，粒子第一次达x轴用时△t，水平位移为△x，则 　　　(1分)

若满足，则从电场射出时的速度方向也将沿x轴正方向 (2分)

解之得：　 (2分)

即AC间y坐标为 (n = 1，2，3，……) (1分)

⑶ 当n=1时，粒子射出的坐标为

当n=2时，粒子射出的坐标为

当n≥3时，沿x轴正方向射出的粒子分布在y₁到y₂之间(如图)y₁到y₂之间的距离为

L= y₁－y₂= 则磁场的最小半径为 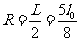　(2分)

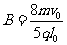若使粒子经磁场偏转后汇聚于一点，粒子的运动半径与磁场圆的半径相等(如图)，(轨迹圆与磁场圆相交，四边形PO₁QO₂为棱形) 由 得：　 (2分)

08高考

如图所示，间距为L的两条足够长的平行金属导轨与水平面的夹角为θ，导轨光滑且电阻忽略不计．场强为B的条形匀强磁场方向与导轨平面垂直，磁场区域的宽度为d₁，间距为d₂．两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上，并与导轨垂直．(设重力加速度为g)

⑴若a进入第2个磁场区域时，b以与a同样的速度进入第1个磁场区域，求b穿过第1个磁场区域过程中增加的动能△E_k；

⑵若a进入第2个磁场区域时，b恰好离开第1个磁场区域；此后a离开第2个磁场区域时，b 又恰好进入第2个磁场区域．且a．b在任意一个磁场区域或无磁场区域的运动时间均相．求b穿过第2个磁场区域过程中，两导体棒产生的总焦耳热Q；

⑶对于第⑵问所述的运动情况，求a穿出第k个磁场区域时的速率v．