
366. 在正方体ABCD-A1B1C1D1中,期棱长为a.
(1)求证BD⊥截面AB1C;
(2)求点B到截面AB1C的距离;
(3)求BB1与截面AB1C所成的角的余弦值。
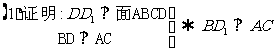
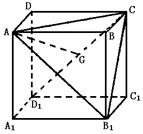
同理BD1⊥AB1.∴BD1⊥面ACB1.
(2)AB=BC=BB1 G为△AB1C的中心.AC=
G为△AB1C的中心.AC=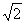 a
a
AG=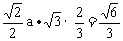 a
a
∴BG=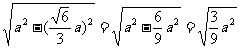 =
=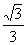 a
a
(3)∠BB1G为所求
cos∠BB1G=
365. 设棱锥M-ABCD的底面是正方形,且MA=MD,MA⊥AB,如果ΔAMD的面积为1,试求能够放入这个棱锥的最大球的半径.
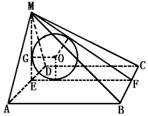
解析: ∵AB⊥AD,AB⊥MA,
∴AB⊥平面MAD,
由此,面MAD⊥面AC.
记E是AD的中点,
从而ME⊥AD.
∴ME⊥平面AC, ME⊥EF
设球O是与平面MAD、AC、平面MBC都相切的球.
不妨设O∈平面MEF,于是O是ΔMEF的内心.
设球O的半径为r,则r=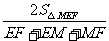
设AD=EF=a,∵SΔAMD=1.
∴ME=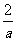 .MF=
.MF=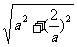 ,
,
r=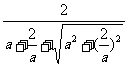 ≤
≤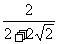 =
=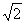 -1
-1
当且仅当a=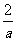 ,即a=
,即a=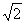 时,等号成立.
时,等号成立.
∴当AD=ME=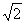 时,满足条件的球最大半径为
时,满足条件的球最大半径为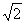 -1.
-1.
364. 在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为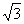 米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
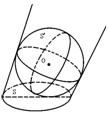
解析:由题意知,光线与地面成60°角,设球的阴影部分面积为S,垂直于光线的大圆面积为S′,则Scos30°=S′,并且S′=9π,所以S=6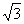 π(米2)
π(米2)
363. 湖结冰时,一个球漂在其上,取出后(未弄破冰),冰面上留下了一个直径为24cm,深为8cm的空穴,求该球的半径.
解析:设球的半径为R,依题意知截面圆的半径r=12,球心与截面的距离为d=R-8,由截面性质得:r2+d2=R2,即122+(R-8)2=R2.
得R=13 ∴该球半径为13cm.
362. 若四面体各棱长是1或2,且该四面体不是正四面体,则其体积的值是 .(只须写出一个可能的值)
解析: 该题的显著特点是结论发散而不惟一.本题表面上是考查锥体求积公式这个知识点,实际上主要考查由所给条件构造一个四面体的能力,首先得考虑每个面的三条棱是如何构成的.
排除{1,1,2},可得{1,1,1},{1,2,2},{2,2,2},然后由这三类面在空间构造满足条件的一个四面体,再求其体积.
由平时所见的题目,至少可构造出二类满足条件的四面体,五条边为2,另一边为1,对棱相等的四面体.
对于五条边为2,另一边为1的四面体,参看图1所示,设AD=1,取AD的中点为M,平面BCM把三棱锥分成两个三棱锥,由对称性可知AD⊥面BCM,且VA-BCM=VD-BCM,所以
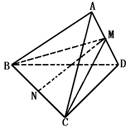
VABCD=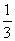 SΔBCM·AD.
SΔBCM·AD.
CM=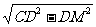 =
=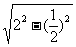 =
=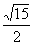 .设N是BC的中点,则MN⊥BC,MN=
.设N是BC的中点,则MN⊥BC,MN=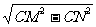 =
=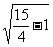 =
=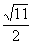 ,从而SΔBCM=
,从而SΔBCM=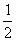 ×2×
×2×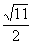 =
=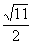 ,
,
故VABCD=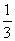 ×
×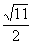 ×1=
×1=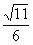 .
.
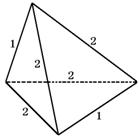
对于对棱相等的四面体,可参见图2.其体积的计算可先将其置于一个长方体之中,再用长方体的体积减去四个小三棱锥的体积来进行.亦可套公式V=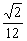 ·
·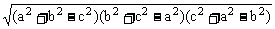 ,
,
不妨令a=b=2,c=1,则
V=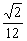 ·
·
=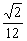 ·
·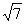 =
=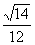 .
.
361. 有一个三棱锥和一个四棱锥,棱长都相等,将它们一个侧面重叠后,还有几个暴露面?
解析:有5个暴露面.
如图所示,过V作VS′∥AB,则四边形S′ABV为平行四边形,有∠S′VA=∠VAB=60°,从而ΔS′VA为等边三角形,同理ΔS′VD也是等边三角形,从而ΔS′AD也是等边三角形,得到以ΔVAD为底,以S′与S重合.
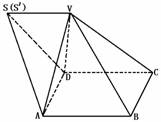
这表明ΔVAB与ΔVSA共面,ΔVCD与ΔVSD共面,故共有5个暴露面.
21.(本小题满分13分)
设函数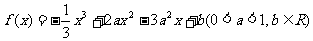
(Ⅰ)求函数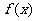 的单增区间和极值;
的单增区间和极值;
(Ⅱ)若对任意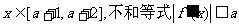 恒成立,求a的取值范围。
恒成立,求a的取值范围。
20.设数列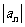 的前n项和
的前n项和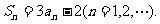
(Ⅰ)求数列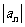 的通项公式;
的通项公式;
(Ⅱ)若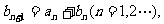 且b1=-3,求数列
且b1=-3,求数列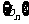 的前n项和Tn
的前n项和Tn
19.(本小题满分13分)
已知椭圆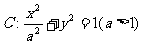 的上顶点为A,左右焦点分别为F1、F2,直线AF2与圆
的上顶点为A,左右焦点分别为F1、F2,直线AF2与圆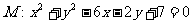 相切。
相切。
(Ⅰ)求椭圆的方程;
(Ⅱ)若椭圆C内的动点P,使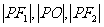 成等比数列(O为坐标原点,)求
成等比数列(O为坐标原点,)求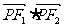 的取值范围。
的取值范围。
18.(本小题满分12分)
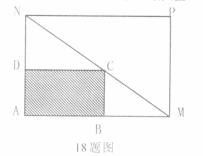
某建筑工地在一块长AM=30米,宽AN=20米的矩形地块AMPN上施工,规划建设占地如图中矩形ABCD的学生公寓,要求顶点C在地块的对角线MN上,B,D分别在边AM,AN上,假设AB长度为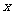 米。
米。
(Ⅰ)要使矩形学生公寓ABCD的面积不小于144平方米,AB的长度应在什么范围?
(Ⅱ)长度AB和宽度AD分别为多少米时矩形学生公寓ABCD的面积最大?最大值是多少平方米?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com