
21.(本小题满分14分)
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.
(1)求证:函数y=f(x)与y=g(x)的图象有两个交点;
(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围;
(3)求证:当x≤-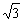 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).
20.(本小题满分12分)
已知定点Q(6,0)和抛物线y2=8x上的两个动点A(x1,y1)、B(x2,y2),其中A、B的横坐标x1、x2满足x1≠x2,且x1+x2=4.
(I)证明线段AB的垂直平分线过定点Q;
(Ⅱ)当A、B两点的距离为何值时,△AQB的面积最大?
19.(本小题满分12分)
某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建设面积为1000平方米,球场的总建筑面积的每平方米的平均建设费用与球场数有关,当该球场建x个时,每平方米的平均建设费用用f(x)表示,且f(n)=f(m)(1+ )(其中n>m,n∈N),又知建五座球场时,每平方米的平均建设费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),公司应建几个球场?
)(其中n>m,n∈N),又知建五座球场时,每平方米的平均建设费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和),公司应建几个球场?
(16)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知 ,
, ,于A处测得水深
,于A处测得水深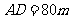 ,于B处测得水深
,于B处测得水深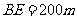 ,于C处测得水深
,于C处测得水深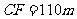 ,求∠DEF的余弦值。 21世纪教育网
,求∠DEF的余弦值。 21世纪教育网
(17)如图,在三棱锥 中,⊿
中,⊿ 是等边三角形,∠PAC=∠PBC=90 º
是等边三角形,∠PAC=∠PBC=90 º
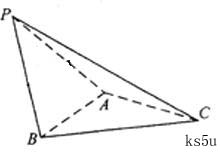 (Ⅰ)证明:AB⊥PC
(Ⅰ)证明:AB⊥PC
(Ⅱ)若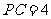 ,且平面
,且平面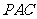 ⊥平面
⊥平面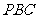 ,
,
求三棱锥 体积。
体积。
18.(本小题满分12分)
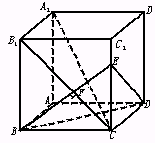 已知长方体AC1中,棱AB=BC=3,棱BB1=4,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
已知长方体AC1中,棱AB=BC=3,棱BB1=4,连结B1C,过B点作B1C的垂线交CC1于E,交B1C于F.
(1)求证A1C⊥平面EBD;
(2)求点A到平面A1B1C的距离;
(3)求平面A1B1C与平面BDE所成角的度数;
(4)求ED与平面A1B1C1所成角的大小;
15. 五位同学围成一圈依序循环报数,规定:
①第一位同学首次报出的数为1.第二位同学首次报出的数也为1,之后每位同学所报出的数都是前两位同学所报出的数之和;
②若报出的是为3的倍数,则报该数的同学需拍手一次,21世纪教育网
当第30个数被报出时,五位同学拍手的总次数为 。
14. 若曲线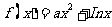 存在垂直于
存在垂直于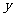 轴的切线,则实数
轴的切线,则实数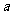 的取值范围是
的取值范围是
13. 点A为周长等于3的圆周上的一个定点,若在该圆周上随机取一点B,则劣弧 AB的长
AB的长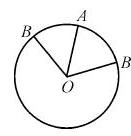 度小于1的概率为
。
度小于1的概率为
。
12. 复数 的实部是
。
的实部是
。
11.在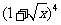 的展开式中,
的展开式中, 的系数为
(用数字作答). 21世纪教育网
的系数为
(用数字作答). 21世纪教育网
10.若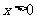 ,则
,则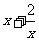 的最小值为
的最小值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com