
2.(2006江西).已知集合 ,
,
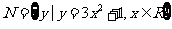 则
则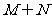 等于 ( )
等于 ( )
A.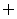 B.
B. 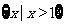 C.
C. 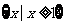 D.
D. 
1.(2006福建)已知全集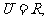 且
且 ,
,
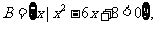 则
则 等于
等于
(A)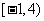 (B)
(B) (C)
(C)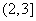 (D)
(D)
6.高次不等式的解法:分解因式,用穿根法.
5.分式不等式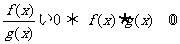 (带等号时分母不为0)
(带等号时分母不为0)
4.含参数的不等式ax +bx+c>0问题一般要分类讨论,具体解法是:
+bx+c>0问题一般要分类讨论,具体解法是:
(1)看 ; (2)
; (2)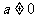 时,先看能否分解因式求方程的根,否则再按
时,先看能否分解因式求方程的根,否则再按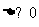 分类讨论;
分类讨论;
(3)看两根大小,依二次函数图象与出不等式的解集。
3.一元二次函数、方程、不等式的的关系:
二次函数 ,与相应的方程
,与相应的方程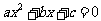 ,不等式
,不等式 有如下关系:(解二次不等式的依据)
有如下关系:(解二次不等式的依据)
|
|
 |
 |
 |
二次函数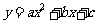 ( ( )的图象 )的图象 |
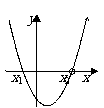 |
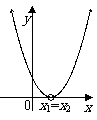 |
 |
一元二次方程 |
有两相异实根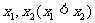 |
有两相等实根 |
无实根 |
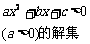 |
 |
 |
R |
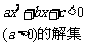 |
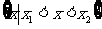 |
 |
 |
对于 的情况可以化为
的情况可以化为 的情况解决
的情况解决
2.解含绝对值不等式的关键是去绝对值符号,去绝对值符号的方法有:
(1)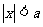
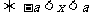 ;
;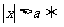
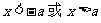
可用于解形如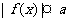 的不等式,(式中a>0,对a≤0时也成立)
的不等式,(式中a>0,对a≤0时也成立)
(2)平方去绝对值:( ,次数不高时)
,次数不高时)
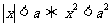 ;
;
注意: 。
。
(3)分段去绝对值:根据绝对值定义,按绝对值符号里面式子的正负号分段去掉绝对值符号。
有些含绝对值不等式需要用到换元法。
1.一元一次不等式 的解集:
的解集:
① ②
②
3.掌握简单的分式不等式,初步了解简单高次不等式的解法。
2.理解一元二次函数、方程、不等式的关系,掌握图象法解一元二次不等式的方法以及含参数的不等式的讨论;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com