
1 解含绝对值不等式,一般是去掉绝对值符号,将其转化为一般的不等式(组)或用换元法来解,所以关键是掌握去绝对值符号的方法;
解含绝对值不等式,一般是去掉绝对值符号,将其转化为一般的不等式(组)或用换元法来解,所以关键是掌握去绝对值符号的方法;
2 解一元二次不等式,要将一元二次不等式与相应的一元二次方程和二次函数结合起来,根据二次函数的图像写出解集;
解一元二次不等式,要将一元二次不等式与相应的一元二次方程和二次函数结合起来,根据二次函数的图像写出解集;
3.如果二次不等式的系数含有字母,则应该根据情况予以讨论,如开口方向,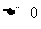 ,两根的大小等;
,两根的大小等;
[例1]解不等式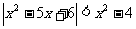
解:(1)当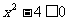 时,不等式的解集为
时,不等式的解集为
(2)当 即
即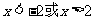 时,有
时,有
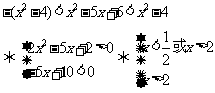
解集为{x|x>2}
[例2] 已知A={x|x3+3x2+2x>0},B={x|x2+ax+b≤0}且A∩B={x|0<x≤2},A∪B={x|x>-2},求a、b的值.
解:A={x|-2<x<-1或x>0},
设B=[x1,x2],由A∩B=(0,2]知x2=2,
且-1≤x1≤0, ①
由A∪B=(-2,+∞)知-2≤x1≤-1. ②
由①②知x1=-1,x2=2,
∴a=-(x1+x2)=-1,b=x1x2=-2.
方法提炼:本题解本题的关键是确定B中方程的两个根,还要熟练掌握在数轴上表示集合(区间)的交与并的方法.
例3.(2007启东中学质检)
解不等式组: ,其中x、y都是整数.
,其中x、y都是整数.
思路点拨: 由绝对值非负及x,y是整数,对y或x作初步限定,再进一步由不等式组求解.
解法一:原不等式组可化为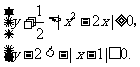
得-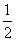 <y<2. ∴y=0或1.
<y<2. ∴y=0或1.
当y=0时, 解得
解得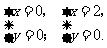
当y=1时,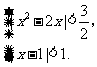 解得
解得 综上,
综上,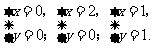
解法二:不等式组化为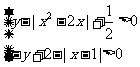 ,两式相加得
,两式相加得
∵x为整数,∴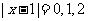
当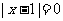 时,x=1,y=1
时,x=1,y=1
当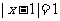 时,
时,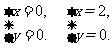
当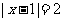 时,无解.
时,无解.
综上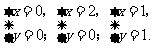
[例4]若不等式 对于x取任何实数均
对于x取任何实数均
成立,求k的取值范围
解:∵4x2+6x+3恒正
∴ 
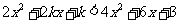
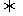
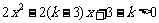 ,
,
∴题设即不等式2x2-2(k-3)x+3-k>0对x取任何实数均成立
∴ =[-2(k-3)]2-8(3-k)<0
=[-2(k-3)]2-8(3-k)<0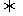 k2-4k+3<0
k2-4k+3<0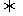 1<k<3
1<k<3
∴k的取值范围是(1,3)。
思路.方法:(1)若非分母符号确定,一般把分式不等式化为一边为零的形式;
(2)不等式恒成立一般方法是:大于须最小值大于,小于须最大值小于。二次式恒>0(或<0)也可利用判别式。
[研讨.欣赏]解关于x的不等式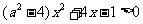
解:原式
当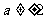 时,方程的根为
时,方程的根为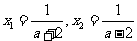 ;
;
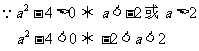
且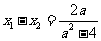 所以
所以
(1)当a<-2时 ,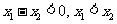
原不等式的解集为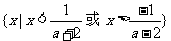
(2)当-2<a<0时, ,原不等式的解集为:
,原不等式的解集为:
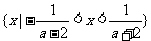 ;
;
(3)当0<a<2时,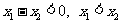 ,原不等式的解集为:
,原不等式的解集为:
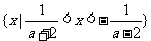
(4)当a>2时, ,原不等式的解集为:
,原不等式的解集为: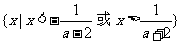
(5)当a=0时,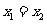 ,原不等式的解集为Φ
,原不等式的解集为Φ
(6) 当a=±2时 ,原不等式的解集为
方法提炼:解含参数二次不等式的分类讨论方法--(见上面建构知识网络)
6、由韦达定理得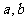 的值
的值
5、法1:用绝对值的几何意义借助数轴分析;
法2:借助于函数的图象,数形结合;
4、分段去绝对值;
3、借助于函数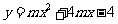 的图象分析;
的图象分析;
6.已知不等式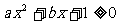 的解集为
的解集为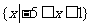 ,则
,则 的值依次是
的值依次是
答案提示:1-3、CBC; 4、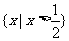 ;5、a>3; 6、
;5、a>3; 6、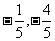
5.关于x的不等式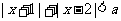 有解,则实数a的取值范围是
有解,则实数a的取值范围是
4. 不等式|x-3|-|x+1|<1的解集为
3.(2004湖北)设集合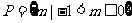 ,Q={
,Q={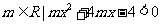 对任意实数都成立},则下列关系中成立的是
( )
对任意实数都成立},则下列关系中成立的是
( )
A.
 Q B.Q
Q B.Q P C.P=Q D.
P C.P=Q D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com