
4.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面
A1B1C1D1的中心,则O到平面AB C1D1的距离为( B )
A、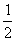 B、
B、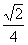 C、
C、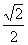 D、
D、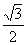
3. 在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角是( D
)
在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角是( D
)
A. 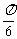 B.
B. 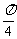 C.
C. 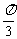 D.
D. 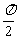
2.长方体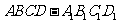 的8个顶点在同一个球面上,且AB=2,AD=
的8个顶点在同一个球面上,且AB=2,AD=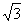 ,
, 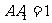 ,则顶点A、B间的球面距离是( B )
,则顶点A、B间的球面距离是( B )
A.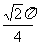 B.
B.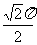 C.
C.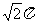 D.2
D.2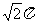
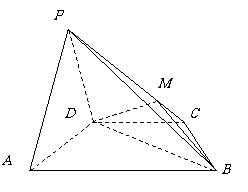 例8.如图,在四棱锥
例8.如图,在四棱锥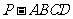 中,平面
中,平面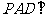 平面
平面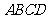 ,
,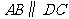 ,
, 是等边三角形,已知
是等边三角形,已知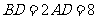 ,
,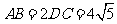 .
.
(Ⅰ)设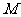 是
是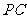 上的一点,证明:平面
上的一点,证明:平面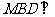 平面
平面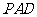 ;
;
(Ⅱ)求四棱锥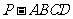 的体积.
的体积.
变式:
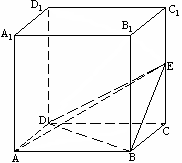 正方体
正方体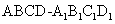 ,
,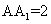 ,E为棱
,E为棱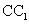 的中点.
的中点.
(Ⅰ)
求证: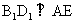 ;
;
(Ⅱ)
求证: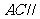 平面
平面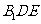 ;
;
(Ⅲ)求三棱锥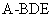 的体积.
的体积.
 反馈练习:
反馈练习:
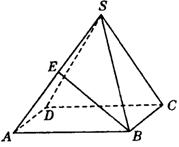
1.如图所示,已知正四棱锥S-ABCD侧棱长为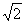 ,底
,底
面边长为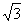 ,E是SA的中点,则异面直线BE与SC
,E是SA的中点,则异面直线BE与SC
所成角的大小为( B )
A.90° B.60° C.45° D.30°
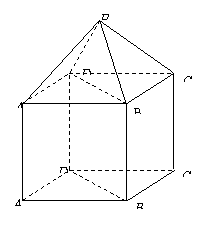
例7.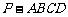 是正四棱锥,
是正四棱锥,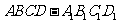 是正方体,其中
是正方体,其中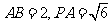 .
.
(Ⅰ)求证: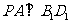 ;
;
 (Ⅱ)求平面
(Ⅱ)求平面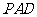 与平面
与平面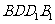 所成的锐二面角
所成的锐二面角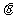 的大小;
的大小;
(Ⅲ)求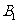 到平面
到平面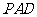 的距离.
的距离.
变式:
如图4,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
(Ⅰ)证明PQ⊥平面ABCD;
(Ⅱ)求异面直线AQ与PB所成的角;
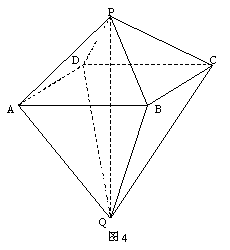 (Ⅲ)求点P到平面QAD的距离.
(Ⅲ)求点P到平面QAD的距离.
例6.已知正方形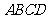
 、
、 分别是
分别是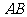 、
、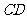 的中点,将
的中点,将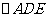 沿
沿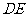 折起,如图所示,记二面角
折起,如图所示,记二面角 的大小为
的大小为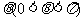
(1) 证明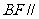 平面
平面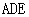 ;
;
(2)若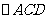 为正三角形,试判断点
为正三角形,试判断点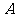 在平面
在平面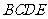 内的射影
内的射影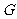 是否在直线
是否在直线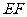 上,证明你的结论,并求角
上,证明你的结论,并求角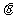 的余弦值。
的余弦值。

变式:
如图,在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=6,BC=3,DC=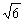 ,A是P1D的中点,E是线段AB的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角.
,A是P1D的中点,E是线段AB的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角.
 (Ⅰ)求证:PA⊥平面ABCD;(Ⅱ)求平面PEC和平面PAD所成的锐二面角的大小.
(Ⅰ)求证:PA⊥平面ABCD;(Ⅱ)求平面PEC和平面PAD所成的锐二面角的大小.
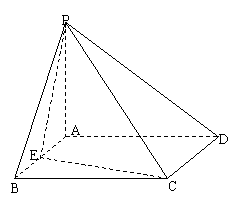
例5.在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
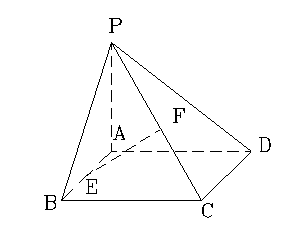 (1)求证:
(1)求证: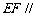 平面PAD;
平面PAD;
(2)当平面PCD与平面ABCD成多大二面角时, 直线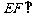 平面PCD?
平面PCD?
变式:
 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=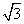 ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
(1)求证:AD^BC
(2)求二面角B-AC-D的大小
(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若不存在,说明理由.
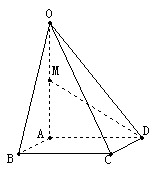 例3.如图,在四棱锥
例3.如图,在四棱锥 中,底面
中,底面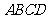 四边长为1的 菱形,
四边长为1的 菱形,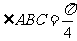 ,
,  ,
, 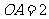 ,
,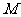 为
为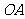 的中点。
的中点。
(Ⅰ)求异面直线AB与MD所成角的大小 ;
;
(Ⅱ)求点B到平面OCD的距离。
例4. 如图,四面体ABCD中,O、E分别BD、BC的中点,CA=CB=CD=BD=2
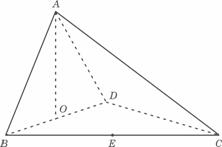 (Ⅰ)求证:AO⊥平面BCD;
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的大小;
(Ⅲ)求点E到平面的距离.
变式:
 如图,正三棱锥
如图,正三棱锥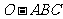 的三条侧棱
的三条侧棱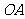 、
、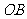 、
、 两两垂直,且长度均为2.
两两垂直,且长度均为2. 、
、 分别是
分别是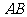 、
、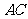 的中点,
的中点,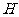 是
是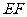 的中点,过
的中点,过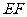 的平面与侧棱
的平面与侧棱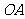 、
、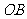 、
、 或其延长线分别相交于
或其延长线分别相交于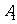 、
、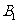 、
、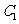 ,已知
,已知 .
.
(1)求证: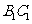 ⊥面
⊥面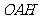 ;
;
(2)求二面角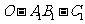 的大小.
的大小.
 题型一、平行与垂直的证明
题型一、平行与垂直的证明
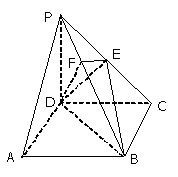
例1.如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明PA//平面EDB;(2)证明PB⊥平面EFD
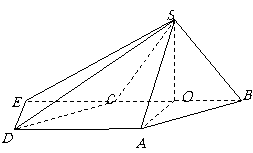 例2.四棱锥
例2.四棱锥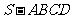 中,底面ABCD为平行四边形,侧面
中,底面ABCD为平行四边形,侧面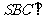 底面ABCD,已知
底面ABCD,已知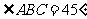 ,
,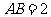 ,
,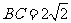 ,
,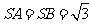 .
.
(Ⅰ)证明: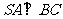 ;
;
(Ⅱ)求直线SD与平面SBC所成角的大小.
变式:
 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,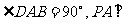 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=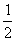 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小.
高考中立体几何主要考查学生的空间想象能力,在推理中兼顾考查逻辑思维能力,解决立体几何的基本方法是将空间问题转化为平面问题。 近几年高考立体几何试题以基础题和中档题为主,热点问题主要有证明点线面的关系,如点共线、线共点、线共面问题;证明空间线面平行、垂直关系;求空间的角和距离;利用空间向量,将空间中的性质及位置关系的判定与向量运算相结合,使几何问题代数化等等。考查的重点是点线面的位置关系及空间距离和空间角,突出空间想象能力,侧重于空间线面位置关系的定性与定量考查,算中有证。其中选择、填空题注重几何符号语言、文字语言、图形语言三种语言的相互转化,考查学生对图形的识别、理解和加工能力;解答题则一般将线面集中于一个几何体中,即以一个多面体为依托,设置几个小问,设问形式以证明或计算为主。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com