
1.3 紧扣二次函数的顶点式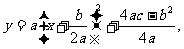 对称轴、最值、判别式显合力
对称轴、最值、判别式显合力
例4 已知函数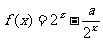 。
。
(1)将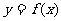 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数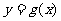 ,求函数
,求函数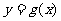 的解析式;
的解析式;
(2)函数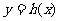 与函数
与函数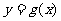 的图象关于直线
的图象关于直线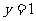 对称,求函数
对称,求函数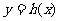 的解析式;
的解析式;
(3)设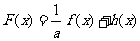 ,已知
,已知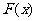 的最小值是
的最小值是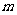 且
且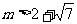 ,求实数
,求实数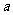 的取值范围。
的取值范围。
解:(1)
(2)设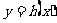 的图像上一点
的图像上一点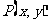 ,点
,点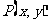 关于
关于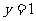 的对称点为
的对称点为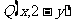 ,由点Q在
,由点Q在 的图像上,所以
的图像上,所以
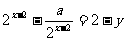 ,
,
于是 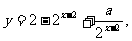
即 
(3)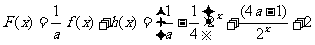 .
.
设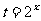 ,则
,则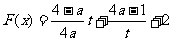 .
.
问题转化为: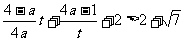 对
对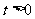 恒成立. 即
恒成立. 即
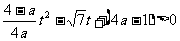 对
对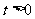 恒成立. (*)
恒成立. (*)
故必有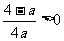 .(否则,若
.(否则,若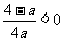 ,则关于
,则关于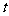 的二次函数
的二次函数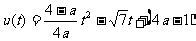 开口向下,当
开口向下,当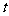 充分大时,必有
充分大时,必有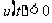 ;而当
;而当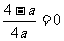 时,显然不能保证(*)成立.),此时,由于二次函数
时,显然不能保证(*)成立.),此时,由于二次函数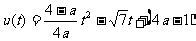 的对称轴
的对称轴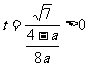 ,所以,问题等价于
,所以,问题等价于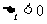 ,即
,即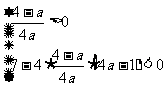 ,
,
解之得: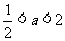 .
.
此时,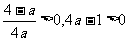 ,故
,故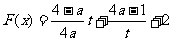 在
在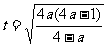 取得最小值
取得最小值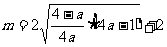 满足条件.
满足条件.
1.2 利用函数与方程根的关系,写出二次函数的零点式
例3 设二次函数 ,方程
,方程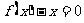 的两个根
的两个根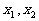 满足
满足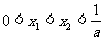 . 当
. 当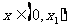 时,证明
时,证明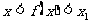 .
.
分析:在已知方程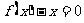 两根的情况下,根据函数与方程根的关系,可以写出函数
两根的情况下,根据函数与方程根的关系,可以写出函数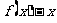 的表达式,从而得到函数
的表达式,从而得到函数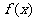 的表达式.
的表达式.
证明:由题意可知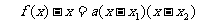 .
.
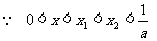 ,
,
∴ 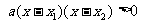 ,
,
∴ 当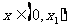 时,
时,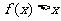 .
.
又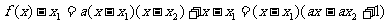 ,
,

∴ 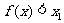 ,
,
综上可知,所给问题获证.
1.1
二次函数的一般式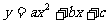
 中有三个参数
中有三个参数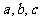 . 解题的关键在于:通过三个独立条件“确定”这三个参数.
. 解题的关键在于:通过三个独立条件“确定”这三个参数.
例1 已知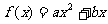 ,满足1
,满足1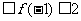 且
且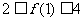 ,求
,求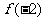 的取值范围.
的取值范围.
分析:本题中,所给条件并不足以确定参数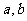 的值,但应该注意到:所要求的结论不是
的值,但应该注意到:所要求的结论不是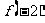 的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1
的确定值,而是与条件相对应的“取值范围”,因此,我们可以把1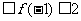 和
和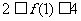 当成两个独立条件,先用
当成两个独立条件,先用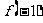 和
和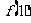 来表示
来表示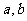 .
.
解:由 ,
,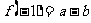 可解得:
可解得:
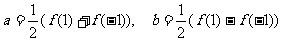 (*)
(*)
将以上二式代入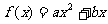 ,并整理得
,并整理得
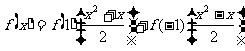 ,
,
∴ 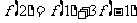 .
.
又∵
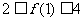 ,
,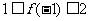 ,
,
∴ 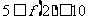 .
.
例2 设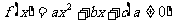 ,若
,若 ,
,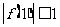 ,
,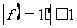 , 试证明:对于任意
, 试证明:对于任意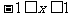 ,有
,有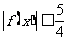 .
.
分析:同上题,可以用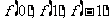 来表示
来表示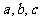 .
.
解:∵ 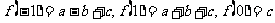 ,
,
∴ 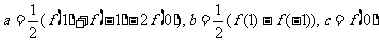 ,
,
∴ 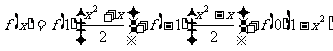 .
.
∴ 当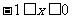 时,
时,

当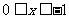 时,
时,
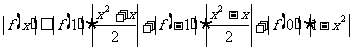
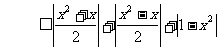
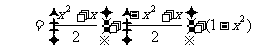
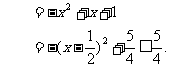
综上,问题获证.
1. 代数推理
由于二次函数的解析式简捷明了,易于变形(一般式、顶点式、零点式等),所以,在解决二次函数的问题时,常常借助其解析式,通过纯代数推理,进而导出二次函数的有关性质.
6、电路故障分析:电路不能正常工作,就是发生了故障,要求掌握断路、短路造成的故障分析。
路端电压随电流的变化图线中注意坐标原点是否都从零开始
电路动态变化分析(高考的热点)各灯、表的变化情况
1程序法:局部变化 R总
R总 I总
I总 先讨论电路中不变部分(如:r)
先讨论电路中不变部分(如:r) 最后讨论变化部分
最后讨论变化部分
局部变化
 再讨论其它
再讨论其它
2直观法:
①任一个R增必引起通过该电阻的电流减小,其两端电压UR增加.(本身电流、电压)
②任一个R增必引起与之并联支路电流I并增加; 与之串联支路电压U串减小(称串反并同法)

当R=r时,电源输出功率最大为Pmax=E2/4r而效率只有50%,
路端电压跟负载的关系
(1)路端电压:外电路的电势降落,也就是外电路两端的电压,通常叫做路端电压。
(2)路端电压跟负载的关系
当外电阻增大时,电流减小,路端电压增大;当外电阻减小时,电流增大,路端电压减小。
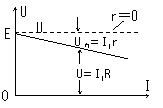 定性分析:R↑→I(=)↓→Ir↓→U(=E-Ir)↑
定性分析:R↑→I(=)↓→Ir↓→U(=E-Ir)↑
R↓→I(=)↑→Ir↑→U(=E-Ir)↓
|
|
|
|
图象描述:路端电压U与电流I的关系图象是一条向下倾斜的直线。U-I图象如图所示。
直线与纵轴的交点表示电源的电动势E,直线的斜率的绝对值表示电源的内阻。
闭合电路中的功率
(1)闭合电路中的能量转化qE=qU外+qU内
在某段时间内,电能提供的电能等于内、外电路消耗的电能的总和。
电源的电动势又可理解为在电源内部移送1C电量时,电源提供的电能。
(2)闭合电路中的功率:EI=U外I+U内I  EI=I2R+I2r
EI=I2R+I2r
说明电源提供的电能只有一部分消耗在外电路上,转化为其他形式的能,另一部分消耗在内阻上,转化为内能。
(3)电源提供的电功率:又称之为电源的总功率。P=EI=
R↑→P↓,R→∞时,P=0。 R↓→P↑,R→0时,Pm=。
(4)外电路消耗的电功率:又称之为电源的输出功率。P=U外I
定性分析:I= U外=E-Ir=
从这两个式子可知,R很大或R很小时,电源的输出功率均不是最大。
 定量分析:P外=U外I==(当R=r时,电源的输出功率为最大,P外max=)
定量分析:P外=U外I==(当R=r时,电源的输出功率为最大,P外max=)
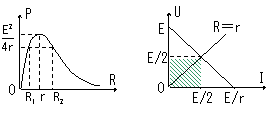
图象表述:
从P-R图象中可知,当电源的输出功率小于最大输出功率时,对应有两个外电阻R1、R2时电源的输出功率相等。可以证明,R1、R2和r必须满足:r=。
(5)内电路消耗的电功率:是指电源内电阻发热的功率。
P内=U内I= R↑→P内↓,R↓→P内↑。
(6)电源的效率:电源的输出功率与总功率的比值。η==
当外电阻R越大时,电源的效率越高。当电源的输出功率最大时,η=50%。
5、含电容器的电路:分析此问题的关键是找出稳定后,电容器两端的电压。
4、滑动变阻器的几种连接方式
a、限流连接:如图,变阻器与负载元件串联,电路中总电压为U,此时负载Rx的电压调节范围红为 ,其中Rp起分压作用,一般称为限流电阻,滑线变阻器的连接称为限流连接。
,其中Rp起分压作用,一般称为限流电阻,滑线变阻器的连接称为限流连接。
b 、分压连接:如图,变阻器一部分与负载并联,当滑片滑动时,两部分电阻丝的长度发生变化,对应电阻也发生变化,根据串联电阻的分压原理,其中UAP= ,当滑片P自A端向B端滑动时,负载上的电压范围为0~U,显然比限流时调节范围大,R起分压作用,滑动变阻器称为分压器,此连接方式为分压连接。
,当滑片P自A端向B端滑动时,负载上的电压范围为0~U,显然比限流时调节范围大,R起分压作用,滑动变阻器称为分压器,此连接方式为分压连接。
一般说来,当滑动变阻器的阻值范围比用电器的电阻小得多时,做分压器使用好;反之做限流器使用好。
3、电路简化原则和方法
①原则:a、无电流的支路除去;b、电势相等的各点合并;c、理想导线可任意长短;d、理想电流表电阻为零,理想电压表电阻为无穷大;e、电压稳定时电容器可认为断路
②方法:a、电流分支法:先将各节点用字母标上,判定各支路元件的电流方向(若无电流可假设在总电路两端加上电压后判定),按电流流向,自左向右将各元件,结点,分支逐一画出,加工整理即可;b、等势点排列法:标出节点字母,判断出各结点电势的高低(电路无电压时可先假设在总电路两端加上电压),将各节点按电势高低自左向右排列,再将各节点间的支路画出,然后加工整理即可。注意以上两种方法应结合使用。
2、记住结论:①并联电路的总电阻小于任何一条支路的电阻;②当电路中的任何一个电阻的阻值增大时,电路的总电阻增大,反之则减小。
I= (定义) I=nesv(微观) I=
(定义) I=nesv(微观) I=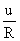 R=
R=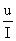 (定义) 电阻定律:R=
(定义) 电阻定律:R=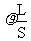 (决定)
(决定)
部分电路欧姆定律: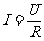
 U=IR
U=IR
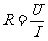 闭合电路欧姆定律:I =
闭合电路欧姆定律:I =

路端电压: U = e -I r= IR 输出功率: 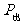 = Iε-I
= Iε-I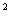 r =
r = 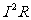
电源热功率: 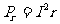 电源效率:
电源效率: 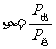 =
=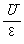 =
=
电功: W=QU=UIt=I2Rt=U2t/R 电功率P==W/t =UI=U2/R=I2R 电热:Q=I2Rt
对于纯电阻电路: W=IUt=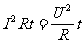 P=IU =
P=IU =
对于非纯电阻电路: W=IUt >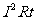 P=IU>
P=IU>
E=I(R+r)=u外+u内=u外+Ir P电源=uIt= +E其它 P电源=IE=I U +I2Rt
单位:J ev=1.9×10-19J 度=kwh=3.6×106J 1u=931.5Mev
电路中串并联的特点和规律应相当熟悉
1、联电路和并联电路的特点(见下表):
|
|
串联电路 |
并联电路 |
|
|
两个基本特点 |
电压 |
U=U1+U2+U3+…… |
U=U1=U2=U3=…… |
|
电流 |
I=I1=I2=I3=…… |
I=I1+I2+I3+…… |
|
|
三个重要性质 |
电阻 |
R=R1+R2+R3+…… |
1/R=1/R1+1/R2+1/R3+……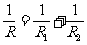 R= R=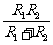 |
|
电压 |
U/R=U1/R1=U2/R2=U3/R3=……=I |
IR=I1R1=I2R2=I3R3=……=U |
|
|
功率 |
P/R=P1/R1=P2/R2=P3/R3=……=I2 |
PR=P1R1=P2R2=P3R3=……=U2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com