
2.(人教版第109页例6)
已知a = (4,2),b = (6,y),且a // b ,求 y .
变式1:与向量a = (12,5) 平行的单位向量为( )
A. B.
B.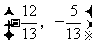
C.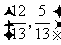 或
或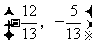 D.
D.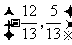 或
或
正确答案:选C
变式2:已知a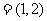 ,b
,b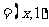 ,当a+2b与2a-b共线时,
,当a+2b与2a-b共线时,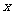 值为 ( )
值为 ( )
A.1
B.2
C.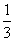 D.
D.
正确答案:选D
变式3:已知A(0,3) 、B(2,0) 、C(-1,3)
与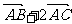 方向相反的单位向量是( )
方向相反的单位向量是( )
A.(0,1) B.(0,-1) C. (-1,1) D.(1,-1)
正确答案:选A
变式4:已知a = (1,0),b = (2,1) .试问:当k为何实数时, ka-b与a+3b平行, 平行时它们是同向还是反向?
解:因为 ka-b 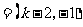 ,a+3b
,a+3b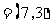 .
.
由已知得,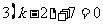 解得
解得 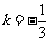 ,
,
此时,ka-b 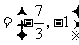 ,a+3b
,a+3b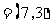 ,二者方向相反.
,二者方向相反.
4.(人教版第102页第13题)
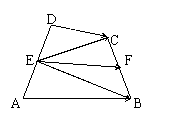 已知四边形ABCD,点E、F、G、H分别是AB、BC、CD、DA的中点,求证:
已知四边形ABCD,点E、F、G、H分别是AB、BC、CD、DA的中点,求证: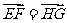
变式1:已知任意四边形ABCD的边AD和BC的中点分别为E、F,
求证: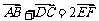 .
.
证明:如图,连接EB和EC ,
由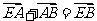 和
和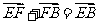 可得,
可得,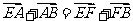 (1)
(1)
由 和
和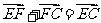 可得,
可得,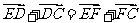 (2)
(2)
(1)+(2)得, 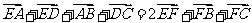 (3)
(3)
∵E、F分别为AD和BC的中点,∴ ,
,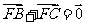 ,
,
代入(3)式得,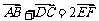
3.(人教版第98页例6)
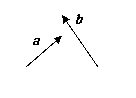 如图,已知任意两个非零向量a 、b ,试作
如图,已知任意两个非零向量a 、b ,试作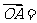 a + b,
a + b,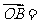 a + 2b,
a + 2b,
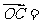 a + 3b,你能判断A、B、C三点之间的位置关系吗?为什么?
a + 3b,你能判断A、B、C三点之间的位置关系吗?为什么?
变式1:已知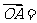 a + 2b,
a + 2b,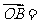 2a +
4b,
2a +
4b,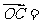 3a +
6b
(其中a 、b是两个任意非零向量) ,证明:A、B、C三点共线.
3a +
6b
(其中a 、b是两个任意非零向量) ,证明:A、B、C三点共线.
证明:∵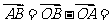 a + 2b,
a + 2b,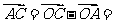 2a +
4b,
2a +
4b,
∴ 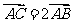 所以,A、B、C三点共线.
所以,A、B、C三点共线.
变式2:已知点A、B、C在同一直线上,并且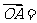 a + b,
a + b,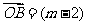 a + 2b,
a + 2b,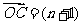 a + 3b (其中a 、b是两个任意非零向量) ,试求m、n之间的关系.
a + 3b (其中a 、b是两个任意非零向量) ,试求m、n之间的关系.
解: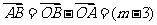 a + b ,
a + b ,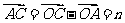 a + 2b
a + 2b
由A、B、C三点在同一直线上可设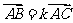 ,
,
则 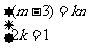 所以
所以 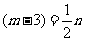 即
即  为所求.
为所求.
2.(人教版第96页例4)
 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,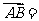 a ,
a , b ,
b ,
你能用a,b表示向量 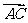 ,
,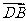 吗?
吗?
变式1:如图,在五边形ABCDE中,
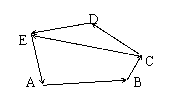
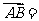 a ,
a ,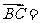 b ,
b ,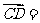 c ,
c ,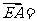 d ,
d ,
试用a ,b , c , d表示向量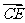 和
和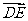 .
.
解: ( a + b + d )
( a + b + d )
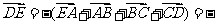 ( d + a + b +c )
( d + a + b +c )
变式2:如图,在平行四边形ABCD中,若,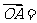 a ,
a ,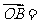 b
b
则下列各表述是正确的为( )
A.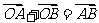 B.
B.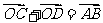
C.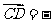 a + b D.
a + b D.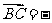 (a + b)
(a + b)
正确答案:选D
变式3:已知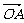 =a,
=a, =b,
=b, 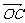 =c,
=c,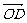 =d, 且四边形ABCD为平行四边形,则( )
=d, 且四边形ABCD为平行四边形,则( )
A. a+b+c+d=0 B. a-b+c-d=0
C. a+b-c-d=0 D. a-b-c+d=0
正确答案:选A
变式4:在四边形ABCD中,若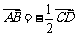 ,则此四边形是( )
,则此四边形是( )
A.平行四边形 B.菱形 C.梯形 D.矩形
正确答案:选C
变式5:已知a、b是非零向量,则|a|=|b|是(a+b)与(a-b)垂直的 ( )
A.充分但不必要条件 B.必要但不充分条件
? C.充要条件 D.既不充分也不必要条件
正确答案:选C
变式6:在四边形ABCD中, =a+2b,
=a+2b,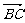 =-4a-b,
=-4a-b,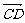 =-5a-3b,其中a、b不共线,则四边形ABCD为( )
=-5a-3b,其中a、b不共线,则四边形ABCD为( )
A.平行四边形 B.矩形 C.梯形 D.菱形
[解析] ∵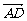 =
=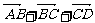 =-8a-2b=2
=-8a-2b=2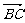 ,∴
,∴ .
.
∴四边形ABCD为梯形.
正确答案:选C
变式7:已知菱形ABCD,点P在对角线AC上(不包括端点A、C),则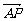 等于( )
等于( )
A.λ( +
+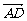 ),λ∈(0,1) B.λ(
),λ∈(0,1) B.λ( +
+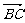 ),λ∈(0,
),λ∈(0,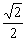 )
)
C.λ( -
-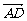 ),λ∈(0,1) D.λ(
),λ∈(0,1) D.λ(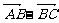 ),λ∈(0,
),λ∈(0,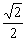 )
)
[解析] 由向量的运算法则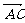 =
= +
+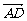 ,而点P在对角线AC上,所以
,而点P在对角线AC上,所以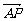 与
与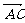 同向,且|
同向,且|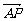 |<|
|<|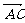 |,∴
|,∴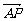 =λ(
=λ( +
+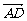 ),λ∈(0,1).
),λ∈(0,1).
正确答案:选 A
变式8:已知D、E、F分别是△ABC的边BC、CA、AB的中点,且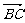 =
=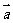 ,
,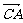 =
=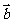 ,
, =
=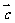 ,则下列各式: ①
,则下列各式: ① =
=
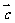 -
-
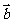 ②
②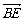 =
=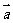 +
+
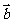
③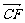 =-
=-
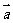 +
+
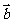 ④
④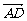 +
+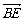 +
+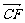 =
=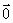
其中正确的等式的个数为( )
A.1 B.2 C.3 D.4
正确答案:选B
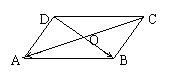
1.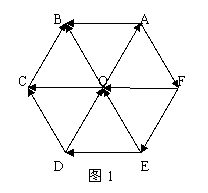 (人教版P85例2)
(人教版P85例2)
如图1,设O是正六边形的中心,分别写出
图中与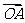 、
、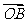 、
、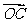 相等的向量。
相等的向量。
变式1:
如图1,设O是正六边形的中心,分别写出
 图中与
图中与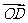 、
、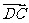 共线的向量。
共线的向量。
解:
变式2:
如图2,设O是正六边形的中心,分别写出
图中与 的模相等的向量以及方向相同的向量。
的模相等的向量以及方向相同的向量。
解:
命题人:越秀区教育发展中心 余建炜
2.3 因为二次函数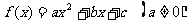 在区间
在区间 和区间
和区间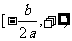 上分别单调,所以函数
上分别单调,所以函数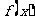 在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数
在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数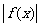 在闭区间上的最大值必在区间端点或顶点处取得.
在闭区间上的最大值必在区间端点或顶点处取得.
例7 已知二次函数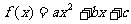 ,当
,当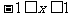 时,有
时,有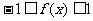 ,求证:当
,求证:当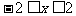 时,有
时,有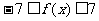 .
.
分析:研究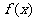 的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数
的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数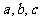 . 确定三个参数,只需三个独立条件,本题可以考虑
. 确定三个参数,只需三个独立条件,本题可以考虑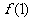 ,
,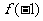 ,
,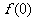 ,这样做的好处有两个:一是
,这样做的好处有两个:一是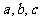 的表达较为简洁,二是由于
的表达较为简洁,二是由于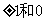 正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
要考虑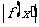 在区间
在区间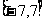 上函数值的取值范围,只需考虑其最大值,也即考虑
上函数值的取值范围,只需考虑其最大值,也即考虑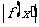 在区间端点和顶点处的函数值.
在区间端点和顶点处的函数值.
解:由题意知: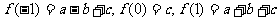 ,
,
∴ 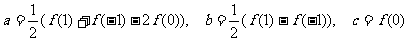 ,
,
∴ 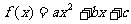
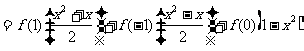 .
.
由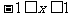 时,有
时,有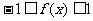 ,可得
,可得 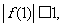
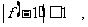
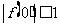 .
.
∴ 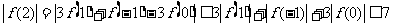 ,
,
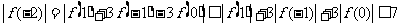 .
.
(1)若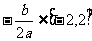 ,则
,则 在
在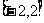 上单调,故当
上单调,故当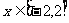 时,
时,
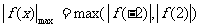
∴ 此时问题获证.
(2)若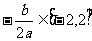 ,则当
,则当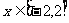 时,
时,
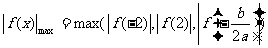
又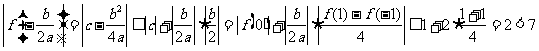 ,
,
∴ 此时问题获证.
综上可知:当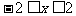 时,有
时,有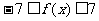 .
.
2.2 二次函数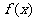 的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数
的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数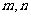 使得
使得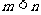 且
且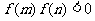
 在区间
在区间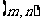 上,必存在
上,必存在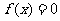 的唯一的实数根.
的唯一的实数根.
例6 已知二次函数 ,设方程
,设方程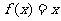 的两个实数根为
的两个实数根为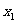 和
和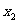 .
.
(1)如果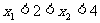 ,设函数
,设函数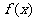 的对称轴为
的对称轴为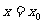 ,求证:
,求证: ;
;
(2)如果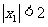 ,
,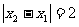 ,求
,求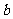 的取值范围.
的取值范围.
分析:条件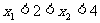 实际上给出了
实际上给出了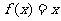 的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.
的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.
解:设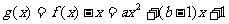 ,则
,则 的二根为
的二根为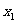 和
和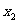 .
.
(1)由 及
及 ,可得
,可得 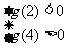 ,即
,即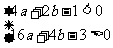 ,即
,即
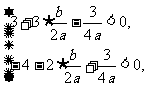
两式相加得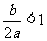 ,所以,
,所以, ;
;
(2)由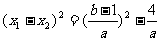 , 可得
, 可得 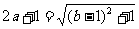 .
.
又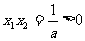 ,所以
,所以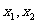 同号.
同号.
∴ 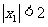 ,
,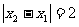 等价于
等价于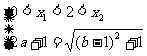 或
或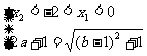 ,
,
即 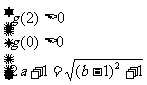 或
或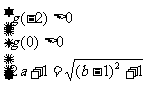
解之得 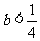 或
或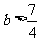 .
.
2.1 二次函数的图像关于直线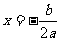 对称, 特别关系
对称, 特别关系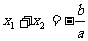 也反映了二次函数的一种对称性.
也反映了二次函数的一种对称性.
例5 设二次函数 ,方程
,方程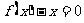 的两个根
的两个根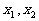 满足
满足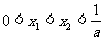 . 且函数
. 且函数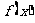 的图像关于直线
的图像关于直线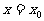 对称,证明:
对称,证明: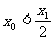 .
.
解:由题意
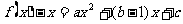 .
.
由方程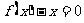 的两个根
的两个根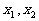 满足
满足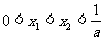 , 可得
, 可得
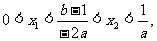 且
且 ,
,
∴  ,
,
即 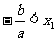 ,故
,故 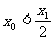 .
.
2. 数形结合
二次函数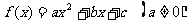 的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.
的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com