
6. 如图,在正方体
如图,在正方体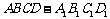 中,P是侧面
中,P是侧面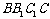 内一动点,若P到直线BC与直线
内一动点,若P到直线BC与直线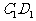 的距离相等,则动点P的轨迹所在的曲线是( )
的距离相等,则动点P的轨迹所在的曲线是( )
A. 直线 B. 圆 C. 双曲线 D. 抛物线
5.从长度分别为1,2,3,4的四条线段中,任取三条的不同取法共有n种,在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则 等于( )
等于( )
A. 0 B.
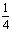 C.
C.
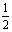 D.
D.
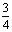
4.已知a、b、c满足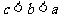 ,且
,且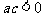 ,那么下列选项中一定成立的是( )
,那么下列选项中一定成立的是( )
A.  B.
B.  C.
C.
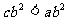 D.
D.

3.设m、n是两条不同的直线,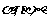 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若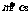 ,
,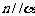 ,则
,则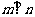 ②若
②若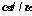 ,
, ,
,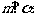 ,则
,则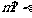
③若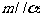 ,
,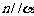 ,则
,则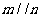 ④若
④若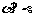 ,
,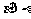 ,则
,则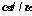
其中正确命题的序号是( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
2.满足条件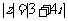 的复数
的复数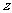 在复平面上对应点的轨迹是( )
在复平面上对应点的轨迹是( )
A. 一条直线 B. 两条直线 C. 圆 D. 椭圆
1.设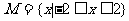 ,
,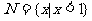 ,则
,则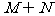 等于( )
等于( )
A. 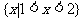 B.
B.
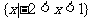 C.
C. 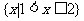 D.
D.
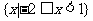
8.(人教A版选修1-1第74页,2-1第85页复习参考题A组第8题)
斜率为2的直线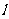 与双曲线
与双曲线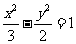 交于A,B两点,且
交于A,B两点,且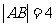 ,求直线的方程.
,求直线的方程.
变式1(2002年上海卷):已知点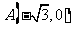 和
和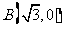 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线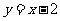 交于D、E两点,求线段DE的长.
交于D、E两点,求线段DE的长.
解:根据双曲线的定义,可知C的轨迹方程为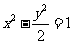 .
.
联立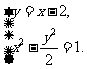 得
得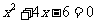 .
.
设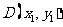 ,
,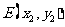 ,则
,则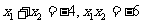 .
.
所以 .
.
故线段DE的长为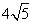 .
.
变式2:直线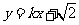 与椭圆
与椭圆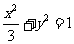 交于不同两点A和B,且
交于不同两点A和B,且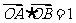 (其中O为坐标原点),求k的值.
(其中O为坐标原点),求k的值.
解:将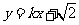 代入
代入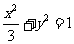 ,得
,得 .
.
由直线与椭圆交于不同的两点,得
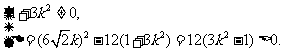 即
即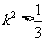 .
.
设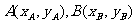 ,则
,则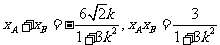 .
.
由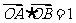 ,得
,得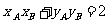 .
.
而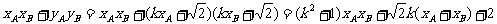
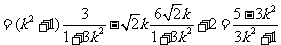 .
.
于是 .解得
.解得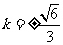 .故k的值为
.故k的值为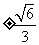 .
.
变式3:已知抛物线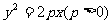 .过动点M(
.过动点M(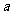 ,0)且斜率为1的直线
,0)且斜率为1的直线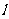 与该抛物线交于不同的两点A、B.若
与该抛物线交于不同的两点A、B.若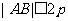 ,求a的取值范围.
,求a的取值范围.
解:直线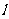 的方程为
的方程为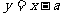 ,
,
将  ,
,
得 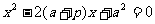 .
.
设直线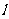 与抛物线的两个不同交点的坐标为
与抛物线的两个不同交点的坐标为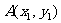 、
、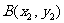 ,
,
则 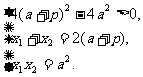
又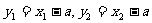 ,
,
∴ 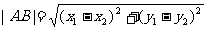

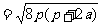 .
.
∵ 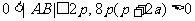 ,
,
∴ 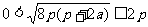 .
.
解得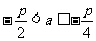 .
.
7.(人教A版选修2-1第67页例5)
过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.
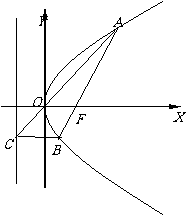 变式(2001年全国卷):设抛物线
变式(2001年全国卷):设抛物线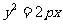 (
(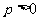 )的焦点为 F,经过点 F的直线交抛物线于A、B两点.点 C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.
)的焦点为 F,经过点 F的直线交抛物线于A、B两点.点 C在抛物线的准线上,且BC∥X轴.证明直线AC经过原点O.
证明1:因为抛物线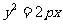 (
(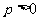 )的焦点为
)的焦点为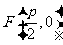 ,所以经过点F的直线AB的方程可设为
,所以经过点F的直线AB的方程可设为
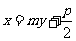 ,代人抛物线方程得
,代人抛物线方程得
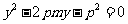 .
.
若记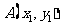 ,
,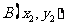 ,则
,则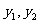 是该方程的两个根,所以
是该方程的两个根,所以
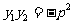 .
.
因为BC∥X轴,且点C在准线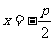 上,所以点C的坐标为
上,所以点C的坐标为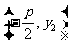 ,
,
 故直线CO的斜率为
故直线CO的斜率为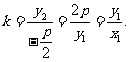
即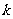 也是直线OA的斜率,所以直线AC经过原点O.
也是直线OA的斜率,所以直线AC经过原点O.
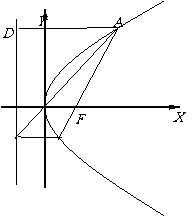
证明2:如图,记X轴与抛物线准线L的交点为E,
过A作AD⊥L,D是垂足.则
AD∥FE∥BC.
连结AC,与EF相交于点N,则
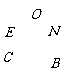
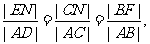
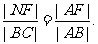
根据抛物线的几何性质,|AF|=|AD|,|BF|=|BC| ,
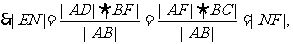
即点N是EF的中点,与抛物线的顶点O重合,所以直线AC经过原点O.
6.(人教A版选修1-1,2-1第66页例4)
斜率为1的直线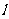 经过抛物线
经过抛物线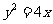 的焦点,且与抛物线相交于A,B两点,求线段AB的长.
的焦点,且与抛物线相交于A,B两点,求线段AB的长.
变式1:如果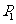 ,
,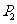 ,…,
,…,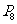 是抛物线
是抛物线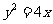 上的点,它们的横坐标依次为
上的点,它们的横坐标依次为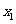 ,
,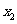 ,…,
,…,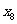 ,F是抛物线的焦点,若
,F是抛物线的焦点,若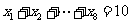 ,则
,则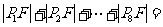 ___.
___.
解:根据抛物线的定义,可知 (
(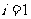 ,2,……,8),
,2,……,8),
∴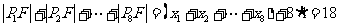 .
.
变式2(2004年湖南卷理):设F是椭圆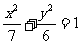 的右焦点,且椭圆上至少有21个不同的点
的右焦点,且椭圆上至少有21个不同的点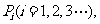 使
使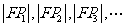 ,组成公差为d的等差数列,则d的取值范围为 .
,组成公差为d的等差数列,则d的取值范围为 .
解:设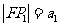 ,则
,则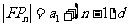 ,于是
,于是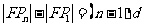 ,即
,即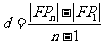 ,由于
,由于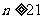 ,
, ,故
,故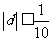 ,又
,又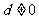 ,故
,故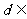
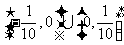 .
.
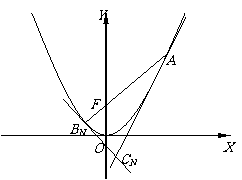 变式3(2006年重庆卷文):如图,对每个正整数
变式3(2006年重庆卷文):如图,对每个正整数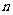 ,
,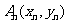 是抛物线
是抛物线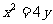 上的点,过焦点
上的点,过焦点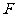 的直线
的直线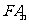 交抛物线于另一点
交抛物线于另一点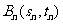 .
.
(Ⅰ)试证: ;
;
(Ⅱ)取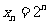 ,并记
,并记 为抛物线上分别以
为抛物线上分别以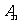 与
与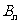 为切点的两条切线的交点.试证:
为切点的两条切线的交点.试证: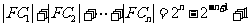 .
.
证明:(Ⅰ)对任意固定的 ,因为焦点
,因为焦点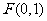 ,所以可设直线
,所以可设直线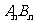 的方程为
的方程为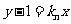 ,将它与抛物线方程
,将它与抛物线方程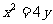 联立,
联立,
得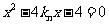 ,由一元二次方程根与系数的关系得
,由一元二次方程根与系数的关系得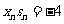 .
.
(Ⅱ)对任意固定的 ,利用导数知识易得抛物线
,利用导数知识易得抛物线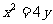 在
在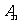 处的切线的斜率
处的切线的斜率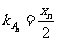 ,故
,故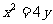 在
在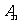 处的切线方程为
处的切线方程为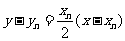 , ①
, ①
类似地,可求得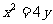 在
在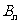 处的切线方程为
处的切线方程为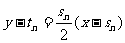 , ②
, ②
由②减去①得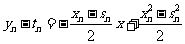 ,
,
从而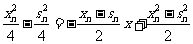 ,
,  ,
,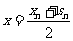 , ③
, ③
将③代入①并注意到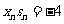 得交点
得交点 的坐标为
的坐标为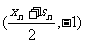 .
.
由两点间距离公式,得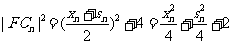
=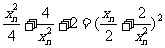 .从而
.从而 .
.
现在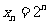 ,利用上述已证结论并由等比数列求和公式得,
,利用上述已证结论并由等比数列求和公式得,
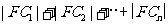
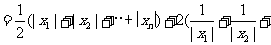 …
…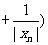
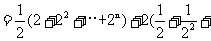 …
…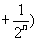
=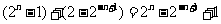 .
.
5.(人教A版选修1-1,2-1第59页习题2.2B组第1题)
求与椭圆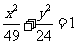 有公共焦点,且离心率
有公共焦点,且离心率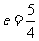 的双曲线的方程.
的双曲线的方程.
变式1(2002年北京卷文):已知椭圆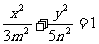 和双曲线
和双曲线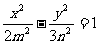 有公共的焦点,那么双曲线的渐近线方程是
有公共的焦点,那么双曲线的渐近线方程是
A.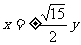 B.
B.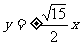 C.
C.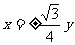 D.
D.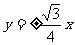
解:依题意,有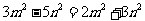 ,即
,即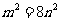 ,即双曲线方程为
,即双曲线方程为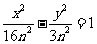 ,故双曲线的渐近线方程是
,故双曲线的渐近线方程是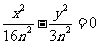 ,即
,即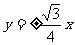 ,选D.
,选D.
变式2(2004年全国卷Ⅳ理):已知椭圆的中心在原点,离心率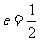 ,且它的一个焦点与抛物线
,且它的一个焦点与抛物线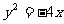 的焦点重合, 则此椭圆方程为( )
的焦点重合, 则此椭圆方程为( )
A.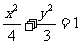 B.
B.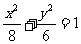
C.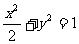 D.
D.
解:∵抛物线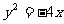 的焦点坐标为(-1,0),则椭圆的
的焦点坐标为(-1,0),则椭圆的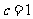 ,又
,又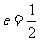 ,则
,则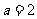 ,进而
,进而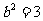 ,所以椭圆方程为
,所以椭圆方程为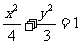 ,选A.
,选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com