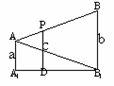
380.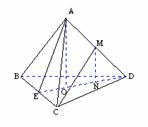 如图，在正四面体ABCD中。各面都是全等的正三角形的四面体，M为AD的中点，求CM与平面BCD所成角的余弦值．

解析：要作出CM在平面BCD内的射影，关键是作出M在平面BCD内的射影，而M为AD的中点，故只需观察A在平面BCD内的射影，至此问题解法已明朗．

解　作AO⊥平面BCD于O，连DO，作MN⊥平面BCD于N，则N∈OD．

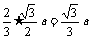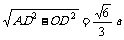设AD＝a，则OD＝，∴AO＝，∴MN＝．

又∵CM＝，∴CN＝．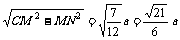

∴CM与平面BCD所成角的余弦值为．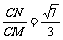

379. Rt△ABC中，∠C＝90°，BC＝36，若平面ABC外一点P与平面A，B，C三点等距离，且P到平面ABC的距离为80，M为AC的中点．

(1)求证：PM⊥AC；

(2)求P到直线AC的距离；

(3)求PM与平面ABC所成角的正切值．

解析：点P到△ABC的三个顶点等距离，则P在平面ABC内的射影为△ABC的外心，而△ABC为直角三角形，其外心为斜边的中点．

证明　(1)∵PA＝PC，M是AC中点，∴PM⊥AC

　　 解　(2)∵BC＝36，∴MH＝18，又PH＝80，

∴PM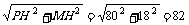＝，即P到直线AC的距离为82；

(3)∵PM=PB=PC，∴P在平面ABC内的射线为△ABC的外心，

　　　 ∵∠C=90°　 ∴P在平面ABC内的射线为AB的中点H。

　　　 ∵PH⊥平面ABC，∴HM为PM在平面ABC上的射影，

则∠PMH为PM与平面ABC所成的角，∴tan∠PMH＝

378. 如图，在正方体ABCD－A₁B₁C₁D₁中，求：

(1)A₁B与平面A₁B₁CD所成的角；

(2)B₁B在平面A₁C₁B所成角的正切值．

解析：　求线面成角，一定要找准斜线在平面内的射影．

(1)先找到斜足A₁，再找出B在平面A₁B₁CD内的射影，即从B向平面A₁B₁CD作垂线，一定要证明它是平面A₁B₁CD的垂线．

这里可证BC₁⊥平面A₁B₁CD，O为垂足，

∴A₁O为A₁B在平面A₁B₁CD上的射影．

(2)若将平面D₁D₁BB竖直放置在正前方，则A₁C₁横放在正前方，估计B₁B在平面A₁C₁B内的射影应落在O₁B上，这是因为A₁C₁⊥平面D₁DBB₁，∴故作B₁H⊥O₁B交于H时，BH₁⊥A₁C₁，即H为B₁在平面A₁C₁B内的射影．另在求此角大小时，只要求∠B₁BO₁即可．

解析：(1)如图，连结BC₁，交B₁C于O，连A₁O．　

∵A₁B₁⊥平面B₁BCC₁，BC₁平面B₁BCC₁，∴A₁B₁⊥BC₁．

又B₁C⊥BC₁，A₁B₁∩B₁C＝B₁，

∴BC₁⊥平面A₁B₁CD，O为垂足，

∴A₁O为A₁B在平面A₁B₁CD上的射影，

则∠BA₁O为A₁B与平面A₁B₁CD所成的角．

sin∠BA₁O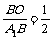＝，∴∠BA₁O＝30°．

(2)连结A₁C₁交B₁D₁于O₁，连BO₁，

作B₁H⊥BO₁于H．∵A₁C₁⊥平面D₁DBB₁，∴A₁C₁⊥B₁H．

又B₁H⊥BO₁，A₁C₁∩BO₁＝O₁，∴B₁H⊥平面A₁C₁B，

∴∠B₁BO₁为B₁B与平面A₁C₁B所成的角，

tan∠B₁BO =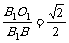，即B₁B与平面A₁C₁B所成的角的正切值为．

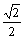377. Rt△ABC中，D是斜边AB的中点，AC＝6，BC＝8，EC⊥平面ABC，且EC＝12，则ED＝　　　．

解析：13．

AB＝10，∴CD＝5，则ED＝＝13．

376. △ABC的三个顶点A，B，C到平面α的距离分别为2cm, 3cm, 4cm , 且它们在α的同一侧，则△ABC的重心到平面α的距离为　　 ．

解析：3cm ．

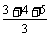＝3cm ．

375. 线段AB的两个端点A，B到平面α的距离分别为6cm, 9cm, P在线段AB上，AP：PB＝1：2，则P到平面α的距离为　　　．

解析：7cm或1cm．

分A，B在平面α的同侧与异侧两种情况．同侧时，P到平面α的距离为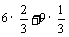＝7(cm)，异侧时，P到平面α的距离为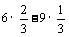＝1(cm)．

374. P为矩形ABCD所在平面外一点，且PA⊥平面ABCD，P到B，C，D三点的距离分别是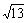，，，则P到A点的距离是　　　　　　　　　　　 (　)

(A)1　　 (B)2　　 (C)　 (D)4　

解析：(A)

设AB＝a，BC＝b，PA＝h，则a²+h²=5, b²+h²=13, a²+b²+h²=17,∴h=1．

373. 定点P不在△ABC所在平面内，过P作平面α，使△ABC的三个顶点到α的距离相等，这样的平面共有　　　　　 　　　　　　 (　)

(A)1个　 (B)2个　 (C)3个　 (D)4个

解析：D

过P作一个与AB，AC都平行的平面，则它符合要求；设边AB，BC，CA的中点分别为E，F，G，则平面PEF符合要求；同理平面PFG，平面PGE符合要求

372. 在正方体ABCD－A₁B₁C₁D₁中，若E是A₁C₁的中点，则直线CE垂直于　　　　　　　　　　　　　　　　 　　 (　)

(A)AC　　 　(B)BD　 　(C)A₁D 　(D)A₁D₁

解析：(B)

BD⊥AC，BD⊥CC₁，∴BD⊥平面A₁ACC₁，∴BD⊥CE．

371. 若两直线a与b异面，则过a且与b垂直的平面　　　　　　　　 (　)

(A)有且只有一个　　　 (B)可能存在也可能不存在

(C)有无数多个　　　　 (D)一定不存在

(B)

解析：若存在，则a⊥b，而由条件知，a不一定与b垂直．