4．功能关系：功和能的关系：功是能量转化的量度。有两层含义：

(1)做功的过程就是能量转化的过程,(2)做功的多少决定了能转化的数量,即:功是能量转化的量度

强调：功是一种过程量，它和一段位移(一段时间)相对应；而能是一种状态量，它与一个时刻相对应。两者的单位是相同的(都是J)，但不能说功就是能，也不能说“功变成了能”。

做功的过程是物体能量的转化过程，做了多少功，就有多少能量发生了变化，功是能量转化的量度．
(1)动能定理	合外力对物体做的总功等于物体动能的增量．即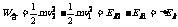
(2)与势能相关力做功导致与之相关的势能变化	重力	重力做正功，重力势能减少；重力做负功，重力势能增加．重力对物体所做的功等于物体重力势能增量的负值．即WG=EP1-EP2= -ΔEP
弹簧弹力	弹力做正功,弹性势能减少；弹力做负功，弹性势能增加． 弹力对物体所做的功等于物体弹性势能增量的负值．即W弹力=EP1-EP2= -ΔEP
分子力	分子力对分子所做的功=分子势能增量的负值
电场力	电场力做正功,电势能减少;电场力做负功,电势能增加。注意：电荷的正负及移动方向 电场力对电荷所做的功=电荷电势能增量的负值
(3)机械能变化原因	除重力(弹簧弹力)以外的的其它力对物体所做的功=物体机械能的增量即WF=E2-E1=ΔE 当除重力(或弹簧弹力)以外的力对物体所做的功为零时，即机械能守恒
(4)机械能守恒定律	在只有重力和弹簧的弹力做功的物体系内，动能和势能可以互相转化，但机械能的总量保持不变．即　 EK2+EP2 = EK1+EP1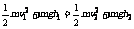， 或　 ΔEK = -ΔEP
(5)静摩擦力做功的特点	(1)静摩擦力可以做正功，也可以做负功，还可以不做功； (2)在静摩擦力做功的过程中，只有机械能的互相转移，而没有机械能与其他形式的能的转化，静摩擦力只起着传递机械能的作用； (3)相互摩擦的系统内，一对静摩擦力对系统所做功的和总是等于零．
(6)滑动摩擦力做功特点 “摩擦所产生的热”	(1)滑动摩擦力可以做正功，也可以做负功，还可以不做功； =滑动摩擦力跟物体间相对路程的乘积，即一对滑动摩擦力所做的功 (2)相互摩擦的系统内，一对滑动摩擦力对系统所做功的和总表现为负功， 其大小为:W= -fS相对=Q　 对系统做功的过程中,系统的机械能转化为其他形式的能， (S相对为相互摩擦的物体间的相对位移;若相对运动有往复性,则S相对为相对运动的路程)
(7)一对作用力与反作用力做功的特点	(1)作用力做正功时，反作用力可以做正功，也可以做负功，还可以不做功；作用力做负功、不做功时，反作用力亦同样如此． (2)一对作用力与反作用力对系统所做功的总和可以是正功,也可以是负功,还可以零．
(8)热学 外界对气体做功	外界对气体所做的功W与气体从外界所吸收的热量Q的和=气体内能的变化W+Q=△U (热力学第一定律,能的转化守恒定律)
(9)电场力做功	W=qu=qEd=F电SE (与路径无关)
(10)电流做功	(1)在纯电阻电路中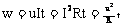(电流所做的功率=电阻发热功率) (2) 在电解槽电路中,电流所做的功率=电阻发热功率+转化为化学能的的功率 (3) 在电动机电路中,电流所做的功率=电阻发热功率与输出的机械功率之和　 P电源t =uIt= +E其它；W=IUt >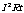
(11)安培力做功	安培力所做的功对应着电能与其它形式的能的相互转化，即W安=△E电， 安培力做正功，对应着电能转化为其他形式的能(如电动机模型)； 克服安培力做功，对应着其它形式的能转化为电能(如发电机模型)； 且安培力作功的绝对值，等于电能转化的量值， W＝F安d＝BILd　 内能(发热)
(12)洛仑兹力永不做功	洛仑兹力只改变速度的方向
(13)光学	光子的能量: E光子=hγ；一束光能量E光=N×hγ(N指光子数目) 在光电效应中，光子的能量hγ=W+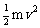
(14)原子物理	原子辐射光子的能量hγ=E初-E末，原子吸收光子的能量hγ= E末-E初 爱因斯坦质能方程：E＝mc2
(15)能量转化和守恒定律	对于所有参与相互作用的物体所组成的系统，其中每一个物体的能量的数值及形式都可能发生变化，但系统内所有物体的各种形式能量的总合保持不变

功和能的关系贯穿整个物理学。现归类整理如下：常见力做功与对应能的关系

3．功与能观点：　

功W = Fs cosq (适用于恒力功的计算)①理解正功、零功、负功②功是能量转化的量度

　 W= P·t　 (p===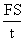Fv) 功率:P = 　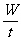(在t时间内力对物体做功的平均功率) P = Fv

(F为牵引力,不是合外力；V为即时速度时,P为即时功率；V为平均速度时,P为平均功率； P一定时，F与V成正比)

动能： E_K=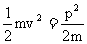　　 重力势能E_p = mgh (凡是势能与零势能面的选择有关)

动能定理：外力对物体所做的总功等于物体动能的变化(增量)。

公式：　 W_合= W_合＝W₁+ W₂+…+W_n= DE_k = E_k2 一E_k1 =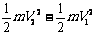 　

机械能守恒定律：机械能=动能+重力势能+弹性势能(条件:系统只有内部的重力或弹力做功).

守恒条件：(功角度)只有重力,弹力做功；(能转化角度)只发生动能与势能之间的相互转化。

“只有重力做功”不等于“只受重力作用”。在该过程中，物体可以受其它力的作用，只要这些力不做功，或所做功的代数和为零，就可以认为是“只有重力做功”。

列式形式：E₁=E₂(先要确定零势面)　 P_减(或增)=E_增(或减)　 E_A减(或增)=E_B增(或减)

mgh₁ +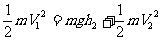 　或者 DE_p减 = DE_k增

除重力和弹簧弹力做功外,其它力做功改变机械能；滑动摩擦力和空气阻力做功W=fd_路程E_内能(发热) 　

2．动量观点：动量：p=mv=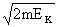　　　　 冲量：I = F t

动量定理：内容：物体所受合外力的冲量等于它的动量的变化。

公式： F_合t = mv^’一mv 　(解题时受力分析和正方向的规定是关键)

I=F_合t=F₁t₁+F₂t₂+---=p=P_末-P_初=mv_末-mv_初

动量守恒定律：内容、守恒条件、不同的表达式及含义：；；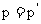

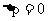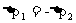
P＝P′　　　　　　　　　　　　 (系统相互作用前的总动量P等于相互作用后的总动量P′)

ΔP＝0　　　　　　　　　　　　 (系统总动量变化为0)

如果相互作用的系统由两个物体构成，动量守恒的具体表达式为

P₁+P₂＝P₁′+P₂′　 　　 (系统相互作用前的总动量等于相互作用后的总动量)

m₁V₁+m₂V₂＝m₁V₁′+m₂V₂′

ΔP＝－ΔP＇　　　　　　　 (两物体动量变化大小相等、方向相反)

实际中应用有：m₁v₁+m₂v₂=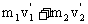； 0=m₁v₁+m₂v₂ m₁v₁+m₂v₂=(m₁+m₂)v_共

原来以动量(P)运动的物体，若其获得大小相等、方向相反的动量(－P)，是导致物体静止或反向运动的临界条件。即：P+(－P)=0

注意理解四性：系统性、矢量性、同时性、相对性

矢量性：对一维情况，先选定某一方向为正方向，速度方向与正方向相同的速度取正，反之取负，把矢量运算简化为代数运算。

相对性:所有速度必须是相对同一惯性参照系。

同时性：表达式中v₁和v₂必须是相互作用前同一时刻的瞬时速度，v₁^’和v₂^’必须是相互作用后同一时刻的瞬时速度。

解题步骤：选对象，划过程；受力分析。所选对象和过程符合什么规律？用何种形式列方程；(先要规定正方向)求解并讨论结果。

1．力的三种效应：

力的瞬时性(产生a)F=ma、运动状态发生变化牛顿第二定律

时间积累效应(冲量)I=Ft、动量发生变化动量定理

空间积累效应(做功)w=Fs动能发生变化动能定理

9．波动模型：特点:传播的是振动形式和能量,介质中各质点只在平衡位置附近振动并不随波迁移。

①各质点都作受迫振动， ②起振方向与振源的起振方向相同， ③离源近的点先振动，

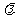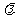④没波传播方向上两点的起振时间差=波在这段距离内传播的时间⑤波源振几个周期波就向外传几个波长。波从一种介质传播到另一种介质,频率不改变, 波速v=s/t=/T=f　 　　

波速与振动速度的区别　 波动与振动的区别：波的传播方向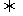质点的振动方向(同侧法)

知波速和波形画经过Δt后的波形(特殊点画法和去整留零法)

物理解题方法：如整体法、假设法、极限法、逆向思维法、物理模型法、等效法、物理图像法等．

模型法常常有下面三种情况

(1)物理对象模型：用来代替由具体物质组成的、代表研究对象的实体系统，称为对象模型(也可称为概念模型)，即把研究的对象的本身理想化．常见的如“力学”中有质点、刚体、杠杆、轻质弹簧、单摆、弹簧振子、弹性体、绝热物质等；

(2)条件模型：把研究对象所处的外部条件理想化，排除外部条件中干扰研究对象运动变化的次要因素，突出外部条件的本质特征或最主要的方面，从而建立的物理模型称为条件模型．

(3)过程模型：把具体过理过程纯粹化、理想化后抽象出来的一种物理过程，称过程模型

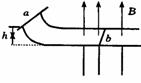
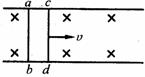
其它的碰撞模型：

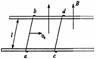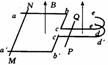8．单摆模型：T=2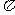 　　(类单摆)　　 利用单摆测重力加速度

7．弹簧振子模型：F=-Kx (X、F、a、v、A、T、f、E_K、E_P等量的变化规律)水平型　 竖直型

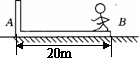
6．人船模型：一个原来处于静止状态的系统，在系统内发生相对运动的过程中，

在此方向遵从动量守恒：mv=MV　　 ms=MS　　 s+S=d　　 s=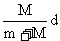　　 M/m=L_m/L_M

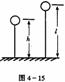
载人气球原静止于高h的高空，气球质量为M，人的质量为m．若人沿绳梯滑至地面，则绳梯至少为多长？

5．碰撞模型：特点，①动量守恒；②碰后的动能不可能比碰前大；

③对追及碰撞，碰后后面物体的速度不可能大于前面物体的速度。

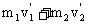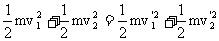◆弹性碰撞：m₁v₁+m₂v₂=(1) 　　(2 )

◆一动一静且二球质量相等的弹性正碰：速度交换

大碰小一起向前；质量相等，速度交换；小碰大，向后返。

◆一动一静的完全非弹性碰撞(子弹打击木块模型)

mv₀+0=(m+M)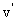　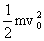 =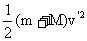+E_损　　

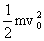E_损=一=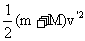

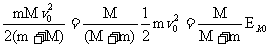
E_损 可用于克服相对运动时的摩擦力做功转化为内能E_损=fd_相=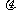mg·d_相=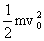一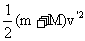

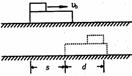
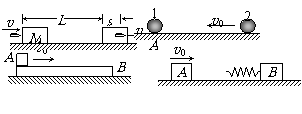
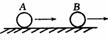
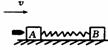
“碰撞过程”中四个有用推论

弹性碰撞除了遵从动量守恒定律外，还具备：碰前、碰后系统的总动能相等的特征，

设两物体质量分别为m₁、m₂，碰撞前速度分别为υ₁^­­、υ₂，碰撞后速度分别为u₁、u₂，即有 ：

　m₁υ₁^­­+m₂υ₂=m₁u₁+m₁u₂

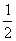　 　m₁υ₁^2­­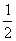+m₂υ₂²=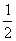m₁u₁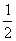²+m₁u₂²

碰后的速度u₁和u₂表示为： u₁=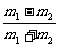υ₁+υ₂

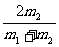u₂=υ₁+υ₂

推论一：如对弹性碰撞的速度表达式进行分析，还会发现：弹性碰撞前、后，碰撞双方的相对速度大小相等，即}：　 u₂－u₁=υ₁－υ₂

推论二：如对弹性碰撞的速度表达式进一步探讨，当m₁=m₂时，代入上式得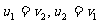：。即当质量相等的两物体发生弹性正碰时，速度互换。

推论三：完全非弹性碰撞碰撞双方碰后的速度相等的特征，即： u­₁=u₂

由此即可把完全非弹性碰撞后的速度u₁和u₂表为：　 u₁=u₂=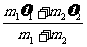

例3：证明：完全非弹性碰撞过程中机械能损失最大。

证明：碰撞过程中机械能损失表为：　 △E=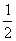m₁υ₁²+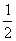m₂υ₂²―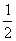m₁u₁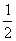²―m₂u₂²

由动量守恒的表达式中得：　　 u₂=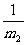(m₁υ₁+m₂υ₂－m₁u₁)

代入上式可将机械能的损失△E表为u₁的函数为：

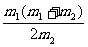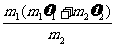△E=－u₁²－u₁+[(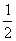m₁υ₁²+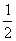m₂υ₂²)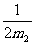－( m₁υ₁+m₂υ₂)²]

这是一个二次项系数小于零的二次三项式，显然：当　　　 u₁=u₂=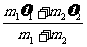时，

即当碰撞是完全非弹性碰撞时，系统机械能的损失达到最大值

△E_m=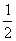m₁υ₁²+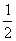m₂υ₂² －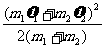

推论四：碰撞过程中除受到动量守恒以及能量不会增加等因素的制约外，还受到运动的合理性要求的制约，比如，某物体向右运动，被后面物体追及而发生碰撞，被碰物体运动速度只会增大而不应该减小并且肯定大于或者等于(不小于)碰撞物体的碰后速度。

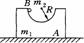
4．超重失重模型　　　　　　　　　　　　　　　　　　　　　　　　　

系统的重心在竖直方向上有向上或向下的加速度(或此方向的分量a_y)

向上超重(加速向上或减速向下)F=m(g+a)；向下失重(加速向下或减速上升)F=m(g-a)

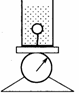难点：一个物体的运动导致系统重心的运动

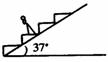1到2到3过程中 (1、3除外)超重状态　　　　　　

绳剪断后台称示数

系统重心向下加速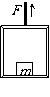

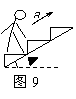
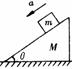斜面对地面的压力?　

地面对斜面摩擦力?　

导致系统重心如何运动？

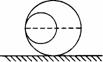
铁木球的运动

用同体积的水去补充