1．下列说法正确的是：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．微粒的布朗运动反映的是花粉分子的无规则运动

　　　 B．微粒的布朗运动反映了液体内部分子的无规则运动

　　　 C．气体压强是由气体内部分子间斥力而产生的

　　　 D．热力学零度不可能达到

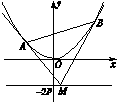
2．如图，设抛物线方程为x²＝2py(p>0)，M为直线y＝－2p上任意一点，过M引抛物线的切线，切点分别为A，B.

　 (1)求证：A，M，B三点的横坐标成等差数列；

　 (2)已知当M点的坐标为(2，－2p)时，|AB|＝4.求此时抛物线的方程；

　 解答：(1)证明：由题意设A(x₁，)，B(x₂，)，x₁<x₂，M(x₀，－2p)．

　 由x²＝2py得y＝，得y′＝，所以k_MA＝，k_MB＝.

　 因此直线MA的方程为y+2p＝(x－x₀)，直线MB的方程为y+2p＝(x－x₀)．

　 所以+2p＝(x₁－x₀)，①

　 +2p(x₂－x₀)．②

　 由①、②得＝x₁+x₂－x₀，因此x₀＝，即2x₀＝x₁+x₂.

　 所以A，M，B三点的横坐标成等差数列．

　 (2)由(1)知，当x₀＝2时，将其代入①、②并整理得：x－4x₁－4p²＝0，x－4x₂－4p²＝0，

　 所以x₁，x₂是方程x²－4x－4p²＝0的两根，因此x₁+x₂＝4，x₁x₂＝－4p²，

　 又k_AB＝＝＝，所以k_AB＝.

　 由弦长公式得|AB|＝＝ .

　 又|AB|＝4，所以p＝1或p＝2，因此所求抛物线方程为x²＝2y或x²＝4y.

1．A、B是抛物线y²＝2px(p＞0)上的两点，且OA⊥OB(O为坐标原点)．求证：

　 (1)A，B的横坐标之积为定值；(2)直线AB经过一定点．

　 证明：(1)设A(x₁，y₁)，B(x₂，y₂)，则有y＝2px₁，y＝2px₂，

　 又∵OA⊥OB，∴x₁x₂+y₁y₂＝0，∵y·y＝4p²x₁x₂，

　 将y₁y₂＝－x₁x₂代入，得xx＝4p²x₁x₂，得知，x₁x₂≠0，

　 ∴x₁x₂＝4p²，故A，B两点横坐标之积为定值4p².

　 (2)∵y－y＝(y₂+y₁)(y₂－y₁)＝2p(x₂－x₁)，x₁≠x₂.∴＝，

　 ∴直线AB的方程为y－y₁＝(x－x₁)，

　 又由x₁＝，得y＝x+y₁－·＝x+，

　 由(1)y₁y₂＝－x₁x₂＝－4p²代入，可得y＝x－＝(x－2p)，

　 所以直线AB过定点(2p,0)．

10．已知椭圆的中心在原点，焦点在x轴上，它的一个焦点为F，M为椭圆上的任意一点，|MF|的最大值和最小值的几何平均数为2，椭圆上存在着以y＝x为对称轴的点M₁和M₂，且|M₁M₂|＝，求椭圆方程．

　 解答：设所求椭圆的方程为+＝1(a>b>0)，

　 M₁、M₂两点的坐标分别为(x₁，y₁)、(y₁，x₁)，x₁>0，则(a+c)(a－c)＝4，即b²＝4，且+＝1，①

　 +＝1，②

　 ①－②得+＝0，

　 ∵x₁≠y₁，∴(－)(x₁+y₁)＝0，∴y₁＝－x₁，|M₁M₂|＝＝2x₁.

　 又|M₁M₂|＝，∴x₁＝.

　 ∴M₁点的坐标为(，－)代入方程+＝1得+＝1，解得a²＝5.

　 因此所求椭圆的方程为+＝1.

★　 选做题

9．过抛物线焦点F的直线交抛物线于P、Q两点，PQ的垂直平分线交抛物线的对称轴于R点，求证：|FR|＝|PQ|.

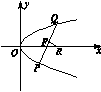　 证明：证法一：如图设抛物线方程为y²＝2px，p＞0则直线PQ的方程为y＝k(x－)，k≠0，设P、Q两点的坐标为(x₁，y₁)，(x₂，y₂)

　 由得k²x²－p(k²+2)x+＝0，

　 ∴Δ＝p²(k²+2)²－4k²＝4p²k²+4p².

　 且x₁+x₂＝，x₁x₂＝，|PQ|＝|x₁－x₂|＝.

　 由＝，得＝k(－)＝k＝.

　 ∴直线PQ垂直平分线的方程为y－＝－，

　 令y＝0，得x＝p+，∴|FR|＝－＝.

　 因此|FR|＝|PQ|.

　 证法二：设P、Q两点坐标为(，y₁)、(，y₂)，由直线PQ过F点可证y₁y₂＝－p²，|PQ|＝ ＝，直线PQ的斜率为＝.

　 ∴直线PQ垂直平分线方程为y－＝－(x－)，

　 令y＝0，得x＝p+，∴|FR|＝(p+)－

　 ＝＝，则|FR|＝|PQ|.

　 证法三：如上图，PQ的中点为M，过P、Q、M分别作PP′、MM′、QQ′垂直于抛物线的准线x＝－，连结M′F、M′P，由抛物线的定义得

　 |MM′|＝(|PP′|+|QQ′|)＝(|PF|+|QF|)＝|PQ|＝|MP|，∴∠M′PM＝∠PM′M＝∠P′PM′.

又|PP′|＝|PF|，PM′为△PM′P′与△PM′F的公共边，∴△PM′P′≌△PM′F，则M′F⊥PQ.

又MR⊥PQ，∵M′F∥MR，又MM′∥FR，∴四边形FRMM′为平行四边形．

∴|FR|＝|MM′|＝|PQ|.

8．已知椭圆的中心在坐标原点O，焦点在坐标轴上，直线y＝x+1与该椭圆交于P和Q，且OP⊥OQ，|PQ|＝，求椭圆方程．

　 解答：设椭圆方程为mx²+ny²＝1(m>0，n>0，且m≠n)，设P(x₁，y₁)，Q(x₂，y₂)．

　 由消去y，整理得(m+n)x²+2nx+n－1＝0，Δ＝4n²－4(m+n)(n－1)>0，

　 即m+n－mn>0，OP⊥OQ等价于x₁x₂+y₁y₂＝0，

　 将y₁＝x₁+1，y₂＝x₂+1代入，整理得2x₁x₂+(x₁+x₂)+1＝0，

　 ∴－+1＝0⇒m+n＝2，①

　 由弦长公式，得2·＝()²，将m+n＝2代入，得mn＝.②

　 解①②得或

　 显然满足Δ>0，故所求椭圆的方程为+＝1或+＝1.

7．倾斜角为的直线交椭圆+y²＝1于A、B两点，则线段AB的中点M的轨迹方程是________．

　 解析：设M(x，y)，A(x₁，y₁)，B(x₂，y₂)，则有+y＝1，①

　 +y＝1，②

　 ①－②得(x₁+x₂)(x₁－x₂)+(y₁+y₂)(y₁－y₂)＝0.③

　 又直线AB的斜率k＝tan＝＝1，∴y₁－y₂＝x₁－x₂.④

　 由中点坐标公式得＝x，＝y，

　 即x₁+x₂＝2x，y₁+y₂＝2y.⑤

　 把④⑤代入到③中得x＝－4y，∴直线方程为x+4y＝0，

　 由　得x²＝.∴x₁＝－，x₂＝.

　 ∴点M的轨迹方程为x+4y＝0(－<x<)．

　 答案：x+4y＝0(－<x<)

6．直线y＝kx－2与抛物线y²＝8x交于A、B不同两点，且AB的中点横坐标为2，则k的　　　　 值是________．　

　 解析：设A(x₁，y₁)、B(x₂，y₂)，由消去y得k²x²－4(k+2)x+4＝0，

　 由题意得∴即k＝2.

　 答案： 2

5．直线y＝kx+1与椭圆+＝1恒有公共点，则m的取值范围是______．

　 解析：∵方程+＝1表示椭圆，∴m>0且m≠5.∵直线y＝kx+1恒过(0,1)点，

　 ∴要使直线与椭圆总有公共点，应有：+≤1，m≥1，∴m的取值范围是m≥1且m≠5.

　 答案： m≥1且m≠5

4．斜率为1的直线l与椭圆+y²＝1相交于A、B两点，则|AB|的最大值为(　)

　 A．2　 　　　　　　　　　　　　　 B.　 　　　　　　　　　　　 C.　 　　　　　　　 D.

　 解析：设椭圆截直线于A(x₁，y₁)，B(x₂，y₂)两点，由消去y，得5x²+8tx+4(t²－1)＝0.则有x₁+x₂＝－t，x₁x₂＝.

　 ∴|AB|＝ |x₁－x₂|＝·＝ ，

　 当t＝0时，|AB|_max＝.

　 答案：C