
3、全集:如果集合S含有我们所要研究的各个集合的全部元素,这个集合就可以看作一个全集,全集通常用U表示
三讲解范例:
例1(1)若S={1,2,3,4,5,6},A={1,3,5},求CSA
(2)若A={0},求证:CNA=N*
(3)求证:CRQ是无理数集
解(1)∵S={1,2,3,4,5,6},A={1,3,5},
∴由补集的定义得CSA={2,4,6}
证明(2)∵A={0},N={0,1,2,3,4,…},N*={1,2,3,4,…}
∴由补集的定义得CNA=N*
证明(3)∵ Q是有理数集合,R是实数集合
∴由补集的定义得CRQ是无理数集合
例2已知全集U=R,集合A={x|1≤2x+1<9},求C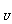 A
A
解:∵A={x|1≤2x+1<9}={x|0≤X<4},U=R
0 4 x
∴C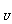 A={x|x<0,或x≥4}
A={x|x<0,或x≥4}
例3 已知S={x|-1≤x+2<8},A={x|-2<1-x≤1},
B={x|5<2x-1<11},讨论A与C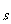 B的关系
B的关系
解:∵S={x|-3≤x<6},A={x|0≤x<3}, B={x|3≤x<6}
∴C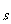 B={x|-3≤x<3}
B={x|-3≤x<3}
∴A C
C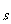 B
B
全集与补集
1 补集:一般地,设S是一个集合,A是S的一个子集(即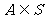 ),
),
由S中所有不属于A的元素组成的集合,叫做S中子集A
 的补集(或余集),记作
的补集(或余集),记作 ,即
,即
CSA=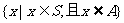
2、性质:CS(CSA)=A ,CSS=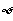 ,CS
,CS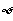 =S
=S
(1)子集:一般地,对于两个集合A与B,如果集合A的任何一
个元素都是集合B的元素,我们就说集合A包含于集
合B,或集合B包含集合A
记作: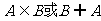 ,A
,A B或B
B或B A
A
读作:A包含于B或B包含A
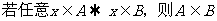
当集合A不包含于集合B,或集合B不包含集合A时,则记
作A B或B
B或B A
A
注: 有两种可能
有两种可能
(1)A是B的一部分,;(2)A与B是同一集合
(2)集合相等:一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,同时集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,记作A=B
(3)真子集:对于两个集合A与B,如果 ,并且
,并且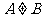 ,我们就说集合A是集合B的真子集,记作:AB或BA, 读作A真包含于B或B真包含A
,我们就说集合A是集合B的真子集,记作:AB或BA, 读作A真包含于B或B真包含A
(4)子集与真子集符号的方向

(5)空集是任何集合的子集Φ A
A
空集是任何非空集合的真子集ΦA 若A≠Φ,则ΦA
任何一个集合是它本身的子集
(6)易混符号
①“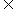 ”与“
”与“ ”:元素与集合之间是属于关系;集合与集合之间是包含关系如
”:元素与集合之间是属于关系;集合与集合之间是包含关系如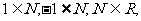 Φ
Φ R,{1}
R,{1} {1,2,3}
{1,2,3}
②{0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合
如
Φ {0}不能写成Φ={0},Φ∈{0}
{0}不能写成Φ={0},Φ∈{0}
(7)含n个元素的集合 的所有子集的个数是
的所有子集的个数是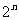 ,所有真
,所有真
子集的个数是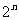 -1,非空真子集数为
-1,非空真子集数为
390. 已知α∩β=C,a∥b,a α,b
α,b β,A
β,A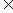 a,AE⊥b于E,AF⊥c于F,求证:a⊥EF
a,AE⊥b于E,AF⊥c于F,求证:a⊥EF
解析: b∥a,b
b∥a,b ,a
,a α, ∴b∥α
α, ∴b∥α
又b β,α∩β=c ∴b∥c, 又AF⊥c ∴AF⊥b
β,α∩β=c ∴b∥c, 又AF⊥c ∴AF⊥b
又AE⊥b, AE∩AF=A ∴b⊥平面AEF a∥b ∴a⊥平面AEF
EF 平面AEF ∴a⊥EF
平面AEF ∴a⊥EF
389. 设P点在正三角形ABC所在平面外,且AP,BP,CP两两垂直;又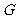 是
是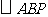 的重心;
的重心;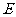 为
为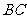 上一点,
上一点,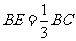 ;
;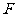 为
为 上一点,
上一点,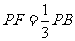 ;
; ,如图
,如图
(1)求证:GF⊥平面PBC;(2)求证:EF⊥BC。
解析:(1)连结BG并延长交PA于M.G为△ABP的重心
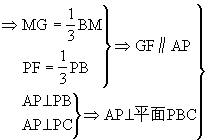
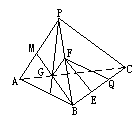
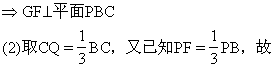
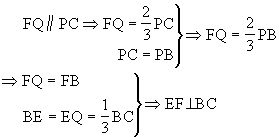
注 要充分注意平面几何中的知识(如本题中三角形重心性质,等腰三角形性质等)在证题中的运用。
388. 如图,在四棱锥P-ABCD中,侧面PCD是边长等于2cm的等边三角形,底面ABCD是面积为2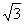 cm2的菱形,∠ADC是锐角.
cm2的菱形,∠ADC是锐角.
求证:PA⊥CD
证明:设∠ADC=θ,则:由SABCD=2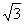 ,
CD=BC=AB=AD=2,易得θ=60°
,
CD=BC=AB=AD=2,易得θ=60°
∴△ACD是等边三角形,取CD中点E连AE、PE,则AE⊥CD,PE⊥CD
AE⊥CD,PE⊥CD ∴CD⊥平面PAE ∴CD⊥PA
387. 如图,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
(1)
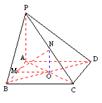 求证:MN⊥CD;
求证:MN⊥CD;
(2) 若∠PDA=45°,求证:MN⊥平面PCD.
证明 (1)连AC∩BD=O,连NO,MO,则NO∥PA.
∵PA⊥平面ABCD,∴NO⊥平面ABCD.
∵MO⊥AB,∴MN⊥AB,而CD∥AB,∴MN⊥CD;
(2)∵∠PDA=45°,∴PA=AD,
由△PAM≌△CBM得PM=CM,
∵N为PC中点,∴MN⊥PC.
 又MN⊥CD,PC∩CD=C,∴MN⊥平面PCD.
又MN⊥CD,PC∩CD=C,∴MN⊥平面PCD.
386. P是边长为a的六边形ABCDEF所成平面外一点,PA⊥AB,PA⊥AF,PA=a,则点P到边CD的距离是
解析:2a.
PA⊥平面ABCDEF,A到CD的距离为 ,∴P到边CD的距离是2a
,∴P到边CD的距离是2a
385. △ABC在平面α内,∠C=90°,点P α,PA=PB=PC=7, AB=10, 则点P到平面α的距离等于
α,PA=PB=PC=7, AB=10, 则点P到平面α的距离等于
解析: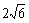 .
.
∵PA=PB=PC,∴P在平面α内的射影为△ABC的外心O,∵∠C=90°,∴O为AB的中点,∵AO=5,PA=7,∴PO=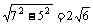
384. 直角三角形ABC的斜边AB在平面α内,直角顶点C在平面α外,C在平面α内的射影为C1,且C1 AB,则△C1AB为 ( )
AB,则△C1AB为 ( )
(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)以上都不对
解析:(C)
∵C1A2+C1B2<CA2+CB2 =AB, ∴∠AC1B为钝角,则△C1AB为钝角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com