
1、函数的单调性是对于函数定义域内的某个子区间而言的,讨论函数的单调性必须在某区间内进行.
[例1] 利用单调性的定义证明函数 在(-∞,+∞)上是减函数。
在(-∞,+∞)上是减函数。
证明:对任意

 ,
, ,
,
即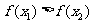 ,
,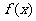 是减函数。
是减函数。
证法二: 对任意
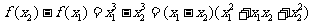
当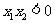 时,有
时,有
当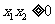 时,有
时,有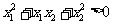

 ,即
,即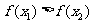 ,
,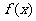 是减函数。
是减函数。
证法三: 对任意
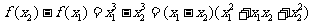

当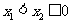 时,有
时,有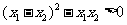 ,又
,又 ,
,
∴ 即
即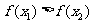 ,
,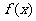 在(-∞,0]上是减函数。同理,
在(-∞,0]上是减函数。同理,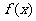 在[0,+∞)上是减函数
在[0,+∞)上是减函数
∴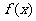 在(-∞,+∞)是减函数。
在(-∞,+∞)是减函数。
特别提醒:要熟练掌握用定义法证明单调性的各种情形和具体手法,本题和下题都是为了强化这一点。
[例2]证明函数y=x+ ,(a>0)的单调区间上的单调性.
,(a>0)的单调区间上的单调性.
解:定义域:{x|x≠0},任取x1、x2∈(0,+∞)且x1<x2,则f(x2)-f(x1)=x2+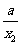 -x1-
-x1-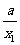 =(x2-x1)+
=(x2-x1)+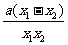 =(x2-x1)(1-
=(x2-x1)(1-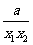 ),
),
(要确定此式的正负只要确定1-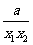 的正负即可.将(0,+∞)分为(0,
的正负即可.将(0,+∞)分为(0, ]与[
]与[ ,+∞)(这是本题的关键)
,+∞)(这是本题的关键)
(1)当x1、x2∈(0, ]时,1-
]时,1-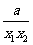 <0,
<0,
∴f(x2)-f(x1)<0,为减函数.
(2)当x1、x2∈[ ,+∞)时,1-
,+∞)时,1- >0,
>0,
∴f(x2)-f(x1)>0,为增函数.
由于f(x)是奇函数,所以在 [- ,0)上递减;在(-∞,-
,0)上递减;在(-∞,- ]上递增.
]上递增.
[例3]已知 若
若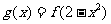 试确定
试确定 的单调区间和单调性
的单调区间和单调性
解:设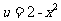 则
则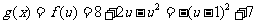
当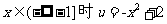 递增,
递增, ,
, 增函数;
增函数;
当 递增,
递增,
 为增函数;
为增函数;
当 递减,
递减,
 为减函数;
为减函数;
当 递增,
递增,
 为增函数;
为增函数;
解: 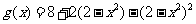
 ,
,
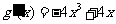 ,
,
令  ,得
,得 或
或 ,
,
令  ,
, 或
或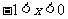
∴单调增区间为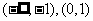 ;单调减区间为
;单调减区间为
方法提炼:按复合函数“同增异减”确定单调性,比较繁琐。本题用导数法求单调区间好。
[例4]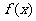 是R上的偶函数,在(-∞.0]上递增,解不等式(1)
是R上的偶函数,在(-∞.0]上递增,解不等式(1)
(2)
解:(1)

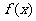 在(-∞.0]上递增,是偶函数,则在[0,+∞)上递减,
在(-∞.0]上递增,是偶函数,则在[0,+∞)上递减,
∴原式
(2)原式
[研究.欣赏]
设函数f(x)=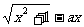 (a>0),求a的取值范围,使函数f(x)在区间[0,+¥)上是单调函数
(a>0),求a的取值范围,使函数f(x)在区间[0,+¥)上是单调函数
解: a³1时,
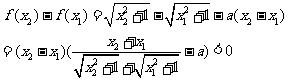
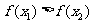 ,f(x)递减;
,f(x)递减;
0<a<1时,存在两点x1=0,x2=2a/(1-a2) ,f(x1)=f(x2)=1,故无单调性
4、当0<a<1时,y=logau递减,u=2-ax递减,复合后递增,当a>1时,增减复合递减,但必须在[0,1]上2-ax>0,只须2-a>0,故1<a<2选B.
6、有下列几个命题:
①函数y=2x2+x+1在(0,+∞)上不是增函数;
②函数y=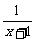 在(-∞,-1)∪(-1,+∞)上是减函数;③函数y=
在(-∞,-1)∪(-1,+∞)上是减函数;③函数y= 的单调区间是[-2,+∞);
的单调区间是[-2,+∞);
④已知f(x)在R上是增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).其中正确命题的序号是_________.
简答精讲:1-4、BAAB;5、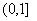 ;6、④
;6、④
5、(2004湖南)若f (x)=
-x2+2ax与 在区间[1,2]上都是减函数,则a的值范围是
在区间[1,2]上都是减函数,则a的值范围是
4、若y=log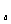 (2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
(2-ax)在[0,1]上是x的减函数,则a的取值范围是( )
A.(0,1) B.(1,2) C.(0,2) D.[2,+∞)
3、 “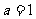 ”是“函数
”是“函数 在区间
在区间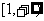 上为增函数”的( )
上为增函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2、(2005上海)若函数f(x)=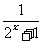 , 则该函数在(-∞,+∞)上是
( )
, 则该函数在(-∞,+∞)上是
( )
A单调递减无最小值 B 单调递减有最小值
C单调递增无最大值 D 单调递增有最大值
1、下列函数中,在区间(0,2)上为增函数的是 ( )
A.y=log2(x2-1 ) B.y=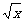 C.y=x2-4x+5 D.y=
C.y=x2-4x+5 D.y=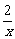
6、一些常用的结论:
①奇函数在其关于原点对称的区间上单调性相同;
②偶函数在其对称区间上的单调性相反;
③单调函数必有反函数,且单调性一致;
④在公共定义域内:
增函数 增函数
增函数 是增函数;
是增函数;
减函数 减函数
减函数 是减函数;
是减函数;
增函数 减函数
减函数 是增函数;
是增函数;
减函数 增函数
增函数 是减函数
是减函数
⑤函数 是奇函数,在
是奇函数,在 和
和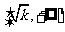 上递增;在
上递增;在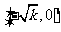 和
和 上是递减,进而可确定
上是递减,进而可确定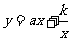 型函数的的单调区间。
型函数的的单调区间。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com