
8、讨论函数f(x)= (a>0)在x∈(-1,1)上的单调性.
(a>0)在x∈(-1,1)上的单调性.
解:设-1<x1<x2<1,
则f(x1)-f(x2)= -
-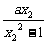
=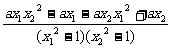 =
=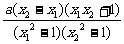 .
.
∵-1<x1<x2<1,∴x2-x1>0,x1x2+1>0,(x12-1)(x22-1)>0.又a>0,∴f(x1)-f(x2)>0,函数f(x)在(-1,1)上为减函数.
7、讨论函数f(x)=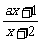 (a≠
(a≠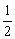 )在(-2,+∞)上的单调性.
)在(-2,+∞)上的单调性.
解:设x1、x2为区间(-2,+∞)上的任意两个值,且x1<x2,则
f(x1)-f(x2)=
=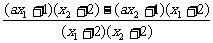
=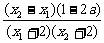 .
.
∵x1∈(-2,+∞),x2∈(-2,+∞)且x1<x2,
∴x2-x1>0,x1+2>0,x2+2>0.
∴当1-2a>0,即a<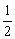 时,f(x1)>f(x2),该函数为减函数;
时,f(x1)>f(x2),该函数为减函数;
当1-2a<0,即a>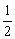 时,f(x1)<f(x2),该函数为增函数.
时,f(x1)<f(x2),该函数为增函数.
6、(2004上海卷)若函数f(x)=a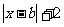 在[0,+∞]上为增函数,则实数a、b的取值范围是 .
在[0,+∞]上为增函数,则实数a、b的取值范围是 .
简答提示
1-4、BCAB;5、(-¥,-3)]、6、数形结合,图象是x=b处为顶点的v字形,当a>0且b≤0时,在[0,+∞]上为增函数;
[解答题]
5、函数y= 的递减区间是
的递减区间是
4、(2005天津卷)若函数 在区间
在区间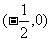 内单调递增,则a的取值范围是
(B )
内单调递增,则a的取值范围是
(B )
A.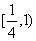 B.
B. 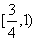 C.
C.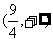 D.
D.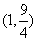
[填空题]
3、函数y=loga(x2+2x-3),当x=2时,y>0,则此函数的单调递减区间是
A.(-∞,-3) B.(1,+∞)
C.(-∞,-1) D.(-1,+∞)
2、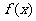 为
为 上的减函数,
上的减函数,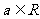 ,则 (
)
,则 (
)
A.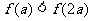 B.
B.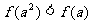
C.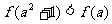 D.
D.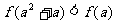
1、下列函数中,在区间 上是增函数的是 (
)
上是增函数的是 (
)
A.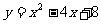 B.
B.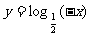
C.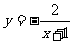 D.
D.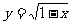
3.解函数单调性的问题时,通常有定义法、图象法、复合函数判断法,导数法,应注意合理选择。
同步练习 2.5函数单调性
[选择题]
2、单调性定义中的x1、x2必须是:同一区间上;任意两个值; x1<x2,三者缺一不可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com