
1.三角函数符号规律记忆口诀:一全正,二正弦,三是切,四余弦;
11.若一阶线性递归数列an=kan-1+b(k≠0,k≠1),则总可以将其改写变形成如下形式: (n≥2),于是可依据等比数列的定义求出其通项公式;
(n≥2),于是可依据等比数列的定义求出其通项公式;
10.对等差数列{an},当项数为2n时,S偶-S奇=nd;项数为2n-1时,S奇-S偶=a中(n∈N*);
9.等差(或等比)数列的“间隔相等的连续等长片断和序列”(如a1+a2+a3,a4+a5+a6,a7+a8+a9…)仍是等差(或等比)数列;
8.若{an}、{bn}是等差数列,则{kan+bbn}(k、b、a是非零常数)是等差数列;若{an}、{bn}是等比数列,则{kan}、{anbn}等也是等比数列;
7.当m+n=p+q(m、n、p、q∈N*)时,对等差数列{an}有:am+an=ap+aq;对等比数列{an}有:aman=apaq;
6.等差数列中, am=an+
(n-m)d,  ; 等比数列中,an=amqn-m; q=
; 等比数列中,an=amqn-m; q= ;
;
5.熟记等差、等比数列的定义,通项公式,前n项和公式,在用等比数列前n项和公式时,勿忘分类讨论思想;
4.首项为正(或为负)的递减(或递增)的等差数列前n项和的最大(或最小)问题,转化为解不等式 解决;
解决;
3.等比数列 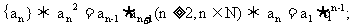
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com