
3.可导与连续的关系:如果函数y=f(x)在点x0处可导,那么函数y=f(x)在点x0处连续;但是y=f(x)在点x0处连续却不一定可导;
2.根据导数的定义,求函数的导数步骤为: (1)求函数的增量
(2)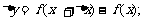 (2)求平均变化率
(2)求平均变化率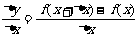 ;
;
(3)取极限,得导数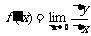 ;
;
1.导数的定义:f(x)在点x0处的导数记作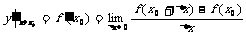 ;
;
5.初等函数的连续性:①指数函数、对数函数、三角函数等都属于基初等函数,基本初等函数在定义域内每一点处都连续;②基本初等函数及常数函数经有限次四则运算和复合后所得到的函数,都是初等函数.初等函数在定义域内每一点处都连续;③连续函数的极限运算:如果函数在点x0处有极限,那么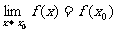 ;
;
4.函数的连续性:(1)如果对函数f(x)在点x=x0处及其附近有定义,而且还有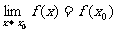 ,就说函数f(x)在点x0处连续;(2)若f(x)与g(x)都在点x0处连续,则f(x)±g(x),f(x)g(x),
,就说函数f(x)在点x0处连续;(2)若f(x)与g(x)都在点x0处连续,则f(x)±g(x),f(x)g(x),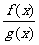 (g(x)≠0)也在点x0处连续;(3)若u(x)在点x0处连续,且f(u)在u0=u(x0)处连续,则复合函数f[u(x)]在点x0处也连续;
(g(x)≠0)也在点x0处连续;(3)若u(x)在点x0处连续,且f(u)在u0=u(x0)处连续,则复合函数f[u(x)]在点x0处也连续;
3.函数的极限:
(1)当x趋向于无穷大时,函数的极限为a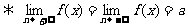
(2)当 时函数的极限为a
时函数的极限为a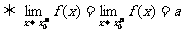 :
:
(3)掌握函数极限的四则运算法则;
2. 数列极限(1)掌握数列极限的直观描述性定义;(2)掌握数列极限的四则运算法则,注意其适用条件:一是数列{an}{bn}的极限都存在;二是仅适用于有限个数列的和、差、积、商,对于无限个数列的和(或积),应先求和(或积),再求极限;(3)常用的几个数列极限: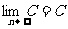 (C为常数);
(C为常数);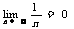 ,
,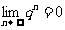 (
( <1,q为常数); (4)无穷递缩等比数列各项和公式
<1,q为常数); (4)无穷递缩等比数列各项和公式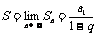 (0<
(0< );
);
1.与自然数有关的命题常用数学归纳法证明,其步骤是:(1)验证命题对于第一个自然数n=n0 (k≥n0)时成立;(2)假设n=k时成立,从而证明当n=k+1时命题也成立,(3)得出结论。数学归纳法是一种完全归纳法,其中两步在推理中的作用是:第一步是递推的基础,第二步是递推的依据,二者缺一不可。第二步证明时要一凑假设,二凑结论;
9.假设检验的基本思想:(1)提出统计假设,确定随机变量服从正态分布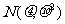 ;(2)确定一次试验中的取值a是否落入范围
;(2)确定一次试验中的取值a是否落入范围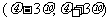 ;(3)作出推断:如果a∈
;(3)作出推断:如果a∈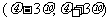 ,接受统计假设;如果a
,接受统计假设;如果a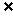
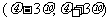 ,由于这是小概率事件,就拒绝假设;
,由于这是小概率事件,就拒绝假设;
8.利用标准正态分布的分布函数数值表计算一般正态分布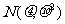 的概率 P(x1<
的概率 P(x1<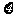 <x2),可由变换
<x2),可由变换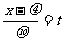 而得
而得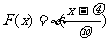 ,于是有P(x1<
,于是有P(x1<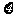 <x2)=
<x2)=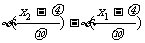 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com