
4.已知向量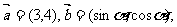 且
且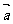 ∥
∥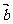 ,则
,则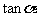 =
=
(A)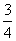 (B)
(B)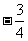 (C)
(C) (D)
(D)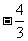
3.已知等差数列 的公差为2,若
的公差为2,若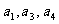 成等比数列, 则
成等比数列, 则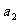 =( )
=( )
(A) –4 (B) –6 (C) –8 (D) –10
2.直线y=2与直线x+y-2=0的夹角是( )
(A)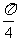 (B)
(B)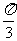 (C)
(C)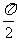 (D)
(D)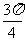
1.若U={1,2,3,4}, M={1,2},N={2,3}, 则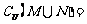 ( )
( )
(A) {1,2,3} (B) {4} (C) {1,3,4} (D) {2}
7.另外:还有数学归纳法、同一法、整体代换法等.
6.反证法
反证法是数学证明的一种重要方法,因为命题p与它的否定非p的真假相反,所以要证一个命题为真,只要证它的否定为假即可。这种从证明矛盾命题(即命题的否定)为假进而证明命题为真的证明方法叫做反证法。
㈠ 反证法证明的一般步骤是:
(1)反设:假设命题的结论不成立,即假设结论的反面成立;
(2)归谬:从命题的条件和所作的结论出发,经过正确的推理论证,得出矛盾的结果;
(3)结论:有矛盾判定假设不正确,从而肯定的结论正确;
㈡ 反证法的适用范围:(1)已知条件很少或由已知条件能推得的结论很少时的命题;
(2)结论的反面是比原结论更具体、更简单的命题,特别是结论是否定形式(“不是”、“不可能”、“不可得”)等的命题;(3)涉及各种无限结论的命题;(4)以“最多(少)、若干个”为结论的命题;(5)存在性命题;(6)唯一性命题;(7)某些定理的逆定理;
(8)一般关系不明确或难于直接证明的不等式等。
㈢ 反证法的逻辑依据是“矛盾律”和“排中律”。
5.分析法、综合法
(1)分析法是从所求证的结果出发,逐步推出能使它成立的条件,直至已知的事实为止;分析法是一种“执果索因”的直接证法。
(2)综合法是从已经证明的结论、公式出发,逐步推出所要求证的结论。综合法是一种“由因导果”,叙述流畅的直接证法。
(3)分析法、 综合法是证明数学问题的两大最基本的方法。分析法“执果索因”的分析方法,思路清晰,容易找到解题路子,但书写格式要求较高,不容易叙述清楚,所以分析法、综合法常常交替使用。分析法、 综合法应用很广,几乎所有题都可以用这两个方法来解。
4.向量法
向量法是运用向量知识解决问题的一种方法,解题常用下列知识:
(1)向量的几何表示,两个向量共线的充要条件;(2)平面向量基本定理及其理论;
(3)利用向量的数量积处理有关长度、角度和垂直的问题;
(4)两点间距离公式、线段的定比分点公式、平移公式;
3.换元法
换元法是指引入一个或几个新的变量代替原来的某些变量(或代数式),对新的变量求出结果之后,返回去求原变量的结果。换元法通过引入新的元素将分散的条件联系起来,或者把隐含的条件显示出来,或者把条件与结论联系起来,或者变为熟悉的问题。其理论根据是等量代换。高中数学中换元法主要有以下两类:
(1)整体换元:以“元”换“式”; (2)三角换元 ,以“式”换“元”;
(3)此外,还有对称换元、均值换元、万能换元等;换元法应用比较广泛。如解方程,解不等式,证明不等式,求函数的值域,求数列的通项与和等,另外在解析几何中也有广泛的应用。运用换元法解题时要注意新元的约束条件和整体置换的策略。
2.待定系数法
㈠ 待定系数法是把具有某种确定性时的数学问题,通过引入一些待定的系数,转化为方程组来解决。待定系数法的主要理论依据是:
(1)多项式f(x)=g(x)的充要条件是:对于任意一个值a,都有f(a)=g(a);
(2)多项式f(x) ≡g(x)的充要条件是:两个多项式各同类项的系数对应相等;
㈡ 运用待定系数法的步骤是:
(1)确定所给问题含待定系数的解析式(或曲线方程等);
(2)根据恒等条件,列出一组含待定系数的方程;
(3)解方程或消去待定系数,从而使问题得到解决;
㈢ 待定系数法主要适用于:求函数的解析式,求曲线的方程,因式分解等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com