2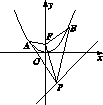．如图，设抛物线C：y＝x²的焦点为F，动点P在直线l：x－y－2＝0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点．

　 (1)求△APB的重心G的轨迹方程；(2)证明∠PFA＝∠PFB.

　 解答：设切点A、B的坐标分别为(x₁，x)，(x₂，x)．

　 (1)由y＝x²知焦点为F(0，)，y′＝2x，

　 则PA，PB的方程分别为2x₁x－y－x＝0,2x₂x－y－x＝0，

　 解方程组得即P(，x₁x₂)，∴－x₁x₂－2＝0①

　 设G(x，y)，则x＝＝②

　 y＝＝③

　 由①②③消去x₁、x₂得y＝；

　 (2)证明：k_AF＝，k_FP＝，tan∠PFA＝＝，

　 同理可求tan∠PFB＝，∴∠PFA＝∠PFB.

　 可检验x₁＝0，或x₁+x₂＝0时，∠PFA＝∠PFB.

1．设A₁、A₂是椭圆+＝1长轴的两个端点，P₁、P₂是垂直于A₁A₂的弦的端点，则直线A₁P₁与A₂P₂交点M的轨迹方程为(　)

　 A.+＝1　 　　　B.+＝1 　　　　C.－＝1　 　　　　D.－＝1

　 解析：如图，设M、P₁、P₂点坐标分别为(x，y)、(x₀，y₀)、(x₀，－y₀)，则+＝1，即＝－.

　 直线A₁P₁的方程为y＝(x+3)①

　 直线A₂P₂的方程为y＝(x－3)②

　 ①×②得y²＝(x²－9)＝(x²－9)，整理得－＝1.

　 答案：C

10．(原创题)如图，已知定点F，定直线l：y＝－，过定直线l上任意一点M作l的垂线MP，线段MF的垂直平分线与直线MP相交于P点．

　 (1)求P点的轨迹C的方程；(2)证明：PN与曲线C相切．

　 解答：(1)由已知条件知|PF|＝|PM|，根据抛物线定义，P点在以F，准线为y＝－的抛物线上，因此点P的轨迹方程为x²＝2py.

　 (2)证明：设M，则k_FM＝－，N，k_NP＝，则直线NP的方程为y＝，将上式代入x²＝2py，整理得：x²－2x₀x+x＝0，则Δ＝－(2x₀)²－4x＝0，

　 因此，直线PN与曲线x²＝2py相切．

9．A、B分别是直线y＝x和y＝－x上的动点．O是坐标原点，且|OA|·|OB|＝a²+b²(a，b为常数值，b≠0)．求线段AB的中点P的轨迹方程．

　 解答：设P、A、B三点的坐标分别为(x，y)、(x₁，y₁)、(x₂，y₂)，则x＝，①

　 y＝，②

　 y₁＝x₁，③

　 y₂＝－x₂，④

　 又|OA||OB|＝ |x₁| |x₂|＝|x₁x₂|，且|OA||OB|＝a²+b²，

　 ∴|x₁x₂|＝a².⑤

　 将③④代入②得y＝(x₁－x₂)，即y＝，⑥

　 ①²－⑥²得x²－y²＝x₁x₂，即x²－y²＝±a².∴所求轨迹方程为－＝±1.

8．已知点F(0，－)，P点在直线y＝－4上方，且P到点F和直线y＝－4的距离之和为.

　 (1)求动点P的轨迹方程；

　 (2)设动点P的轨迹是C，曲线C交y轴于点M，在曲线C上是否存在两点A、B，使∠AMB＝.

　 解答：(1)解法一：如图，设P点坐标为(x，y)，过P作PQ垂直于直线y＝－4，垂足为Q；根据题意得|PF|+|PQ|＝，即 +y+4＝.整理得x²＝－y(y＞－4)．

　 解法二：如图，由|PF|+|PQ|＝可观察出|PF|与P点到直线y＝的距离相等，则P点在以F(0，－)为焦点，O(0,0)为顶点的抛物线x²＝－2py(p＞0)上，∴－＝－，即p＝，∴x²＝－y，

　 又点P在y＝－4上方，则y＞－4.

　 即所求点P的轨迹方程为x²＝－y(y＞－4)．

　 (2)当y＝－1时，x＝±1，因此存在A(－1，－1)，B(1，－1)，使OA·OB＝0，即∠AMB＝.

7．已知圆C：(x－3)²+y²＝4，过原点的直线与圆C相交于A、B两点，则A、B两点中点M的轨迹方程是________．

　 解析：如图，连接CM，则CM⊥AB，因此点M在以OC为直径的圆上，

　 此圆的方程为²+y²＝，

　 将²+y²＝与(x－3)²+y²＝4.相减整理得x＝，

　 因此M点的轨迹方程是²+y²＝，且x＞.

　 答案：²+y²＝

6．设F₁、F₂是双曲线x²－y²＝4的两焦点，Q是双曲线上任意一点，从F₁引∠F₁QF₂平分线的垂线，垂足为P，则P点的轨迹方程是________．

　 解析：如图，延长F₁P交QF₂于F₁′点，连结PO.则在△F₁F₂F₁′中，

　 |PO|＝|F₂F₁′|＝(|QF₁′|－|QF₂|)＝(|QF₁|－|QF₂|)＝2，

　 即|PO|＝2，∴P点的轨迹方程为x²+y²＝4.

　 答案：x²+y²＝4

5．两条直线ax+y+1＝0和x－ay－1＝0(a≠±1)的交点的轨迹方程是________．

　 解析：由

　 ①×y+②×x得　y²+y+x²－x＝0，即(x－)²+(y+)²＝且xy≠0.

　 答案：(x－)²+(y+)²＝，且xy≠0

4．如图，设圆(x+1)²+y²＝25的圆心为C，A(1,0)是圆内一定点，Q为圆周上任一点，线段AQ的垂直平分线与CQ的连线交于点M，则M的轨迹方程为(　)

　 A.－＝1　 　　　　　B.+＝1

　 C.－＝1　 　　　　　D.+＝1

　 解析：M为AQ垂直平分线上一点，则|AM|＝|MQ|，∴|MC|+|MA|＝|MC|+|MQ|＝|CQ|＝5，∴a＝，c＝1，则b²＝a²－c²＝.椭圆的标准方程为+＝1.

　 答案：D