13.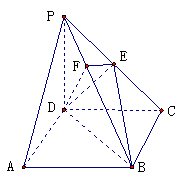 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F

　 (1)证明PA//平面EDB；

(2)证明PB⊥平面EFD；

(3)求二面角C-PB-D的大小

12.已知四棱锥P-ABCD，底面ABCD是菱形，平面ABCD，PD=AD，

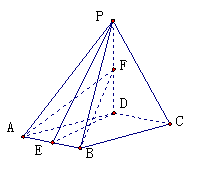点E为AB中点，点F为PD中点.　　　　　　　

　 (1)证明平面PED⊥平面PAB；

　 (2)求二面角P-AB-F的平面角的余弦值.

11.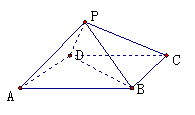 如图，四棱锥P-ABCD中，底面ABCD 为矩形，AB=8，AD=4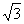，侧面PAD为等边三角形，并且与底面所成二面角为60°.

(Ⅰ)求四棱锥P-ABCD的体积；

(Ⅱ)证明PA⊥BD.

10. 三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3.

(1)求证 AB⊥BC ；

(II)如果 AB=BC=2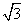，求AC与侧面PAC所成角的大小．

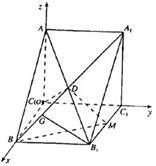
9. 如图，直三棱柱ABC-A₁B₁C₁中，∠ACB＝90^o，AC＝1，CB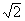＝，侧棱AA₁＝1，侧面AA₁B₁B的两条对角线交点为D，B₁C₁的中点为M．

(Ⅰ)求证：CD⊥平面BDM；

(Ⅱ)求面B₁BD与面CBD所成二面角的大小．

8. 如图，已知四棱锥 P-ABCD，PB⊥AD侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°.

　 (I)求点P到平面ABCD的距离，

(II)求面APB与面CPB所成二面角的大小.

7. 在棱长为4的正方体ABCD-A₁B₁C₁D₁中，O是正方形A₁B₁C₁D₁的中心，点P在棱CC₁上，且CC₁=4CP.

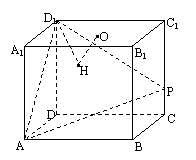(Ⅰ)求直线AP与平面BCC₁B₁所成的角的大小(结果用反三角函数值表示)；

(Ⅱ)设O点在平面D₁AP上的射影是H，求证：D₁H⊥AP；

(Ⅲ)求点P到平面ABD₁的距离.

6.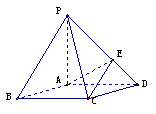 如图，在底面是菱形的四棱锥P-ABCD中，∠ABC=60⁰，PA=AC=a，PB=PD=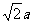,点E在PD上，且PE:ED=2:1.

(I)证明PA⊥平面ABCD；

(II)求以AC为棱，EAC与DAC为面的二面角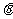的大小；

(Ⅲ)在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.

5.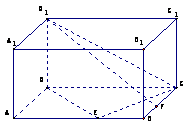 如右下图,在长方体ABCD-A₁B₁C₁D₁中,已知AB= 4, AD =3, AA₁= 2. E、F分别是线段AB、BC上的点，且EB= FB=1.

(1) 求二面角C-DE-C₁的正切值;

(2) 求直线EC₁与FD₁所成的余弦值.

4.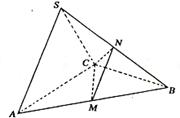 在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2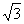，M、N分别为AB、SB的中点.

(Ⅰ)证明：AC⊥SB；

(Ⅱ)求二面角N-CM-B的大小；

(Ⅲ)求点B到平面CMN的距离.