
1. A: ,B:方程
,B:方程
 有实根;
有实根;
3.充要条件:如果 且
且 则p叫做q的
条件.
则p叫做q的
条件.
|
例1.在下列各题中,判断A是B的什么条件,并说明理由.
2.必要条件:如果 则p叫做q的
条件,q叫做p的
条件.
则p叫做q的
条件,q叫做p的
条件.
1.充分条件:如果 则p叫做q的
条件,q叫做p的
条件.
则p叫做q的
条件,q叫做p的
条件.
3.反证法的第一步为否定结论,需要掌握常用词语的否定(如“至少”等),而且推理过程中,一定要把否定的结论当条件用,从而推出矛盾.用反证法证明命题的一般步骤为:(1)假设命题的结论不成立,即假设命题结论的反面成立;(2)从这个假设出发,经过正确的推理论证得出矛盾;(3)由矛盾判断假设不正确,从而肯定所证命题正确.
第2课时 充要条件
|

2.当一个命题直接证明出现困难时,通常采用间接证明法,反证法就是一种间接证法.
1.有关“p或q”与“p且q”形式的复合命题语句中,字面上未出现“或”与“且”字,此时应从语句的陈述中搞清含义从而分清是“p或q”还是“p且q”形式.
3.反证法:欲证“若p则q”为真命题,从否定其 出发,经过正确的逻辑推理导出矛盾,从而判定原命题为真,这样的方法称为反证法.
|
例1. 下列各组命题中,满足“p或q”为真,“p且q”为假,“非p”为真的是 ( )
A.p:0= ;q:0∈
;q:0∈
B.p:在 ABC中,若cos2A=cos2B,则A=B;
ABC中,若cos2A=cos2B,则A=B;  y=sinx在第一象限是增函数
y=sinx在第一象限是增函数
C. ;
; 不等式
不等式 的解集为
的解集为
D.p:圆 的面积被直线
的面积被直线 平分;q:椭圆
平分;q:椭圆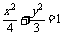 的一条准线方程是x=4
的一条准线方程是x=4
解:由已知条件,知命题p假且命题q真.选项(A)中命题p、q均假,排除;选项(B)中,
命题p真而命题q假,排除;选项(D)中,命题p和命题q都为真,排除;故选(C).
变式训练1:如果命题“p或q”是真命题,“p且q”是假命题.那么( )
A.命题p和命题q都是假命题
B.命题p和命题q都是真命题
C.命题p和命题“非q”真值不同
D.命题q和命题p的真值不同
解: D
例2. 分别写出下列命题的逆命题、否命题、逆否命题,并判断它们的真假:
(1) 若q<1,则方程x2+2x+q=0有实根;
(2) 若ab=0,则a=0或b=0;
(3) 若x2+y2=0,则x、y全为零.
解:(1)逆命题:若方程x2+2x+q=0有实根,则q<1,为假命题.否命题:若q≥1,则方程x2+2x+q=0无实根,为假命题.逆否命题:若方程x2+2x+q=0无实根,则q≥1,为真命题.
(2)逆命题:若a=0或b=0,则ab=0,为真命题.
否命题:若ab≠0,则a≠0且b≠0,为真命题.
逆否命题:若a≠0且b≠0,则ab≠0,为真命题.
(3)逆命题:若x、y全为零,则x2+y2=0,为真命题.
否命题:若x2+y2≠0,则x、y不全为零,为真命题.
逆否命题:若x、y不全为零,则x2+y2≠0,为真命题.
变式训练2:写出下列命题的否命题,并判断原命题及否命题的真假:
(1)如果一个三角形的三条边都相等,那么这个三角形的三个角都相等;
(2)矩形的对角线互相平分且相等;
(3)相似三角形一定是全等三角形.
解:(1)否命题是:“如果一个三角形的三条边不都相等,那么这个三角形的三个角也不都相等”.
原命题为真命题,否命题也为真命题.
(2)否命题是:“如果四边形不是矩形,那么对角线不互相平分或不相等”
原命题是真命题,否命题是假命题.
(3)否命题是:“不相似的三角形一定不是全等三角形”.
原命题是假命题,否命题是真命题.
例3. 已知p: 有两个不等的负根,q:
有两个不等的负根,q: 无实根.若p或q为真,p且q为假,求m的取值范围.
无实根.若p或q为真,p且q为假,求m的取值范围.
分析:由p或q为真,知p、q必有其一为真,由p且q为假,知p、q必有一个为假,所以,“p假且q真”或“p真且q假”.可先求出命题p及命题q为真的条件,再分类讨论.
解:p: 有两个不等的负根.
有两个不等的负根.
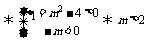
q: 无实根.
无实根.

 因为p或q为真,p且q为假,所以p与q的真值相反.
因为p或q为真,p且q为假,所以p与q的真值相反.
(ⅰ) 当p真且q假时,有 ;
;
(ⅱ) 当p假且q真时,有 .
.
综合,得 的取值范围是{
的取值范围是{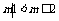 或
或 }.
}.
变式训练3:已知a>0,设命题p:函数y=ax在R上单调递减,q:不等式x+|x-2a|>1的解集为R,若p和q中有且只有一个命题为真命题,求a的取值范围.
解 : 由函数y=ax在R上单调递减知0<a<1,所以命题p为真命题时a的取值范围是0<a<1,令y=x+|x-2a|,
则y=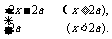 不等式x+|x-2a|>1的解集为R,只要ymin>1即可,而函数y在R上的最小值为2a,所以2a>1,即a>
不等式x+|x-2a|>1的解集为R,只要ymin>1即可,而函数y在R上的最小值为2a,所以2a>1,即a>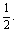 即q真
即q真 a>
a>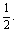 若p真q假,则0<a≤
若p真q假,则0<a≤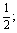 若p假q真,则a≥1,所以命题p和q有且只有一个命题正确时a的取值范围是0<a≤
若p假q真,则a≥1,所以命题p和q有且只有一个命题正确时a的取值范围是0<a≤ 或a≥1.
或a≥1.
例4. 若a,b,c均为实数,且a=x2-2y+ ,b=y2-2z+
,b=y2-2z+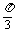 ,c=z2-2x+
,c=z2-2x+ .求证:a、b、c中至少有一个大于0.
.求证:a、b、c中至少有一个大于0.
证明:假设 都不大于0,即
都不大于0,即
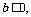
 ,则
,则
而
=
 ,
, .
.
 相矛盾.因此
相矛盾.因此 中至少有一个大于0.
中至少有一个大于0.
变式训练4:已知下列三个方程:①x2+4ax-4a+3=0,②x2+(a-1)x+a2=0,③x2+2ax-2a=0中至少有一个方程有实根,求实数a的取值范围.
解:设已知的三个方程都没有实根.
则
解得 .
.
|
 .
.
2.四种命题的关系:原命题为真,它的逆命题 、否命题 、逆否命题 .原命题与它的逆否命题同 、否命题与逆命题同 .
1.四种命题:原命题:若p则q;逆命题: 、否命题: 逆否命题: .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com