2．从手中竖直向上抛出的小球，与水平天花板碰撞后又落回到手中，设竖直向上的方向为正方向，小球与天花板碰撞时间极短．若不计空气阻力和碰撞过程中动能的损失，则下列图像中能够描述小球从抛出到落回手中整个过程运动规律的是( 　C　 )

1.　　　 如图所示为一个质点作直线运动的v-t图像，下列说法中正确的是(　 D　 )

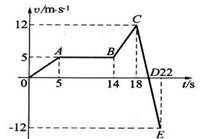(A)在18s~22s时间内，质点的位移为24m

(B)整个过程中，BC段的加速度最大

(C)整个过程中，E点所表示的状态是离出发点最远

(D)BC段表示质点通过的位移为34m

3．已知函数f(x)＝x³+ax+b定义在区间[－1,1]上，且f(0)＝f(1)，设x₁，x₂∈[－1,1]且x₁≠x₂.

(1)求证：|f(x₁)－f(x₂)|<2|x₁－x₂|；

(2)若0<x₁<x₂≤1，求证：|f(x₁)－f(x₂)|<1.

证明：(1)由f(0)＝f(1)，得b＝1+a+b，解得a＝－1.故f(x)＝x³－x+b，设x₁，x₂∈[－1,1]．

则|f(x₁)－f(x₂)|＝|x－x₁－x+x₂|＝|x₁－x₂|·|x+x₁x₂+x－1|.

因为－1≤x₁，x₂≤1，则0≤x≤1,0≤x≤1，－1≤x₁x₂≤1，所以－1≤x+x+x₁x₂≤3，

当且仅当x₁＝x₂＝±1时，右边取等号．∵x₁≠x₂，∴右边等号取不到．

若x+x+x₁x₂＝－1，则x+x+(x₁x₂+1)＝0.

∵x₁x₂+1≥0，∴x₁＝x₂＝0且x₁x₂+1＝0矛盾，∴左边等号也取不到．

所以两边等号均不成立．所以－1<x+x+x₁x₂<3.

所以－2<x+x+x₁x₂－1<2.所以|x+x+x₁x₂－1|<2，

即|f(x₁)－f(x₂)|<2|x₁－x₂|.

(2)因为f′(x)＝3x²－1，令f′(x)＝0，则x＝.由导数的知识容易验证，

当x＝时，[f(x)]_min＝b－.又f(1)＝b，所以当x∈(0,1]时，b－≤f(x)≤b.

则b－≤f(x₁)≤b，b－≤f(x₂)≤b.因为x₁≠x₂，所以f(x₁)≠f(x₂)．所以－≤f(x₁)－f(x₂)≤.即|f(x₁)－f(x₂)|≤.又<1，所以|f(x₁)－f(x₂)|<1.

2．已知数列{a_n}的各项都是正数，且满足：a₀＝1，a_n+1＝a_n·(4－a_n)(n∈N)．

证明：a_n<a_n+1<2(n∈N)．

证明：证法一：用数学归纳法证明：

(1)当n＝0时，a₀＝1，a₁＝a₀(4－a₀)＝，所以a₀<a₁<2，命题正确．

(2)假设n＝k－1(k∈N^*)时命题成立，即a_k－1<a_k<2.

则当n＝k时，a_k－a_k+1

＝a_k－1(4－a_k－1)－a_k(4－a_k)＝2(a_k－1－a_k)－(a_k－1－a_k)(a_k－1+a_k)

＝(a_k－1－a_k)(4－a_k－1－a_k)．

而a_k－1－a_k<0,4－a_k－1－a_k>0，所以a_k－a_k+1<0.

又a_k+1＝a_k(4－a_k)＝ [4－(a_k－2)²]<2.所以n＝k时命题成立．

由(1)(2)可知，对一切n∈N时有a_n<a_n+1<2.

证法二：用数学归纳法证明：

(1)当n＝0时，a₀＝1，a₁＝a₀(4－a₀)＝，所以0<a₀<a₁<2；

(2)假设n＝k－1(k∈N^*)时有a_k－1<a_k<2成立，令f(x)＝x(4－x)，f(x)在[0,2]上单调递增，所以由假设有：f(a_k－1)<f(a_k)<f(2)，

即a_k－1(4－a_k－1)<a_k(4－a_k)<×2×(4－2)，

也即当n＝k时，a_k<a_k+1<2成立．所以对一切n∈N，有a_k<a_k+1<2.

1．对于任意实数a，b定义运算a*b＝(a+1)(b+1)－1，给出以下结论：①对于任意实数a，b，c，有a*(b+c)＝(a*b)+(a*c)；②对于任意实数a，b，c，有a*(b*c)＝(a*b)*c；③对于任意实数a，有a*0＝a，则以上结论正确的是________．(写出你认为正确的结论的所有序号)

解析：按新定义，可以验证a*(b+c)≠(a*b)+(a*c)，所以①不成立；

而a*(b*c)＝(a*b)*c成立，a*0＝(a+1)(0+1)－1＝a.所以正确的结论是②③.

答案：②③

10．已知数列{a_n}的前n项的和S_n满足S_n＝2a_n－3n (n∈N^*)．

(1)求证{a_n+3}为等比数列，并求{a_n}的通项公式；

(2)数列{a_n}是否存在三项使它们按原顺序可以构成等差数列？若存在，求出一组适合条件的项；若不存在，请说明理由．

证明：(1)∵S_n＝2a_n－3n (n∈N^*)，∴a₁＝S₁＝2a₁－3，∴a₁＝3.

又由得a_n+1＝S_n+1－S_n＝2a_n+1－2a_n－3，

∴a_n+1+3＝2(a_n+3)，∴{a_n+3}是首项为a₁+3＝6，公比为2的等比数列．

∴a_n+3＝6×2^n－1，即a_n＝3(2ⁿ－1)．

(2)解答：假设数列{a_n}中存在三项a_r，a_s，a_t (r<s<t)，它们可以构成等差数列．

由(1)知a_r<a_s<a_t，则2a_s＝a_r+a_t，

∴6(2^s－1)＝3(2^r－1)+3(2^t－1)，即2^s+1＝2^r+2^t，∴2^s+1－r＝1+2^t－r(*)

∵r、s、t均为正整数且r<s<t，∴(*)左边为偶数而右边为奇数，

∴假设不成立，即数列{a_n}不存在三项使它们按原顺序可以构成等差数列．

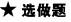
9．如右图所示，O是正方形ABCD的中心，PO⊥底面ABCD，E是PC的中点，求证：平面PAC⊥平面BDE.

证明：∵PO⊥底面ABCD，∴PO⊥BD.

又∵O是正方形的中心，∴BD⊥AC.

∵PO∩AC＝0，∴BD⊥平面PAC，

又BD⊂平面BDE，所以平面PAC⊥平面BDE.

8．试证：当n∈N^*时，f(n)＝3²ⁿ⁺²－8n－9能被64整除．

证明：证法一：(1)当n＝1时，f(1)＝64，命题显然成立．

(2)假设当n＝k(k∈N^*，k≥1)时，f(k)＝3^2k+2－8k－9能被64整除．

当n＝k+1时，由于3^2(k+1)+2－8(k+1)－9

＝9(3^2k+2－8k－9)+9·8k+9·9－8(k+1)－9＝9(3^2k+2－8k－9)+64(k+1)，

即f(k+1)＝9f(k)+64(k+1)，∴n＝k+1时命题也成立．

根据(1)、(2)可知，对于任意n∈N^*，命题都成立．

证法二：(1)当n＝1时f(1)＝64

命题显然成立．

(2)假设当n＝k(k∈N^*，k≥1)时，f(k)＝3^2k+2－8k－9能被64整除．

由归纳假设，设3^2k+2－8k－9＝64m(m为大于1的自然数)，

将3^2k+2＝64m+8k+9代入到f(k+1)中得

f(k+1)＝9(64m+8k+9)－8(k+1)－9＝64(9m+k+1)，∴n＝k+1时命题也成立．

根据(1)(2)知，对于任意n∈N^*，命题都成立．

7．如下图，在杨辉三角形中，从上往下数共有n(n∈N^?)行，在这些数中非1的数字之和是________________．

1

1　1

1　2　1

1　3　3　1

1　4　6　4　1

……

解析：所有数字之和S_n＝2⁰+2+2²+…+2^n－1＝2ⁿ－1，除掉1的和2ⁿ－1－(2n－1)＝2ⁿ－2n.

答案：2ⁿ－2n

6．如果函数f(x)的定义域为R，对于m，n∈R，恒有f(m+n)＝f(m)+f(n)－6，且f(－1)是不小于5的正整数，当x>1时，f(x)<0.那么具有这种性质的函数f(x)＝________.(注：填上你认为正确的一个函数即可)

解析：令m＝n＝0，由f(m+n)＝f(m)+f(n)－6得f(0)＝6，设f(x)＝ax+6，

∵f(－1)＝－a+6≥5.∴a≤1.

又知当x>1时，f(x)<0，∴a<0且f(1)＝a+6≤0.

∴a≤－6 (a∈Z)．∴a＝－6，－7，－8…都符合要求．

答案：－7x+6