
4.∵y=x/5+b的反函数为y=5x-5b,
由已知y=ax+3是y=x/5+b的反函数,
∴函数y=x/5+b与函数y=ax+3为同一个函数,
由此得a=5且-5b=3.
∴a=5,b=-3/5.
1.课本P64习题2.4:3,4.
答案:3.⑴y=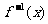 =x/2,
=x/2,
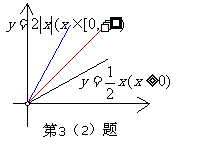 它的定义域为[0,+∞);
它的定义域为[0,+∞);
⑵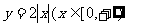
及其反函数
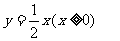
的图象如右图所示.
分段函数的反函数的求法及含有字母的函数的问题
2. 已知函数 =1+
=1+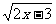 有反函数,且点(a,b)在函数
有反函数,且点(a,b)在函数 的图象上,又在其反函数的图象上,求a,b的值.
的图象上,又在其反函数的图象上,求a,b的值.
解:∵点(a,b)在函数 的图象上,∴b=1+
的图象上,∴b=1+ ---①,
---①,
又点(a,b)在其反函数的图象上,
∴点(b,a)在原函数 的图象上,
的图象上,
∴有a=1+ ---②,联立①②解得a=b=2.
---②,联立①②解得a=b=2.
1.求函数y=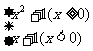 的反函数.
的反函数.
解:当x≥0时,y≥1,由y=x2+1得x=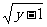 (
y≥1);当x<0时,y<1,由y=x+1得x=y-1(y<1). 将x,y对换得y=
(
y≥1);当x<0时,y<1,由y=x+1得x=y-1(y<1). 将x,y对换得y=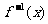 =
=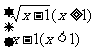 .
.
说明:求分段函数的反函数,应分别求出各段的反函数,再合成.
的值域而得反函数的定义域,这一点绝不能混淆.
例1 求函数y=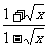 (x≥0,x≠1)的反函数.
(x≥0,x≠1)的反函数.
解:⑴由原函数变形为y-y =1+
=1+ ,即
,即 =(y-1)/(y+1)--①,
=(y-1)/(y+1)--①,
∵ ≥0,∴(y-1)/(y+1)≥0,解得y<-1或y≥1,
≥0,∴(y-1)/(y+1)≥0,解得y<-1或y≥1,
⑵由①两边平方得x=[(y-1)/(y+1)] ,
,
⑶∴原函数的反函数是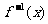 = [(x-1)/(x+1)]
= [(x-1)/(x+1)] (x<-1或x≥1);
(x<-1或x≥1);
说明:原函数的值域是借助于变形中的①式: ≥0而得到的,对于一个比较复杂的函数,求它的值域时要注意题目中的现有条件.
≥0而得到的,对于一个比较复杂的函数,求它的值域时要注意题目中的现有条件.
例2 设函数y= =
=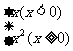 ,求它的反函数.
,求它的反函数.
分析:这里给出了分段函数,即在不同的x范围内有不同的表达式,因此,也应在不同的x范围内求其反函数.
解:⑴当x<0时,y=x,其反函数仍是y=x(x<0);
⑵当x≥0时,y=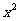 ,由y=
,由y=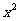 (x≥0)得x=
(x≥0)得x=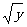 ,又y=
,又y=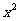 (x≥0)的值域为y≥0,∴y=
(x≥0)的值域为y≥0,∴y=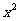 (x≥0)的反函数是y=
(x≥0)的反函数是y= (x≥0).
(x≥0).
⑶由⑴⑵可得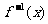 =
=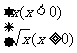 .
.
例3 已知函数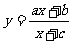 的反函数是
的反函数是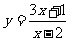 (x∈R,x≠2),求a,b,c的值.
(x∈R,x≠2),求a,b,c的值.
解:⑴由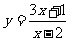 (x≠2)解出x=
(x≠2)解出x= ,
,
∵原函数的值域是y≠3,
∴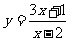 (x≠2)的反函数是
(x≠2)的反函数是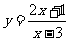 (x≠3,x∈R).
(x≠3,x∈R).
⑵由互为反函数的函数关系知,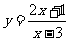 与
与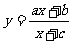 是同一函数,∴a=2,b=1,c=-3.
是同一函数,∴a=2,b=1,c=-3.
例4 若点A(1,2)既在函数 =
=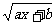 的图象上,又在
的图象上,又在 的反函数的图象上,求a,b的值.
的反函数的图象上,求a,b的值.
分析:求a,b,就要有两个关于a,b的方程,如何寻求?
①A(1,2)在 图象上,这是很容易看出来的.
图象上,这是很容易看出来的.
②如何用它也在 的反函数的图象上呢?
的反函数的图象上呢?
其一,真求反函数,再把A(1,2)代入. 能不能不求反函数?
其二,A(1,2)在反函数图象上,则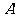 (2,1)就应在原函数的图象上,即(a,b)满足y=
(2,1)就应在原函数的图象上,即(a,b)满足y= ,则(b,a)应满足y=
,则(b,a)应满足y=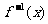 ,反之亦然.
,反之亦然.
解:由A(1,2)在 =
=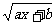 上,则有
上,则有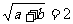 --①;
--①;
由A(1,2)在其反函数图象上,可知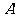 (2,1)也在函数
(2,1)也在函数 =
=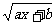 图象上,∴又有
图象上,∴又有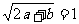 --②,
--②,
解联立①②的方程组得a=-3,b=7.
例5.若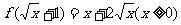 ,试求反函数
,试求反函数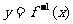 .
.
分析:当已知函数是一个复合函数时,要求它的反函数,首先要求原来函数解析表达式.
解:令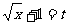 ,则
,则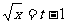 ,
,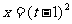 ,
,
代入所给表达式,得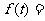
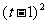 +2
+2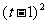 =
=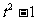 ,
,
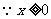 ,∴
,∴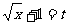
 ,即原来函数是
,即原来函数是 .
.
易求函数 的反函数是
的反函数是
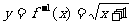
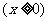 .
.
注:在利用换元解题时,一定要注意新元(中间变量)的取值范围.
2.函数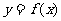 、
、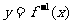 、
、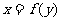 、
、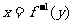 间的关系:
间的关系:
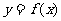 与
与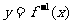 、
、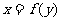 与
与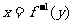 互为反函数;
互为反函数;
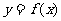 与
与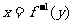 、
、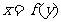 与
与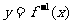 为同一函数
为同一函数
1.反函数的定义;求反函数的一般步骤分:一解、二换、三注明
互为反函数的两个函数有什么关系:
函数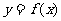 与
与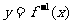 的图象关于直线
的图象关于直线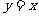 对称.
对称.
反函数的定义域由原函数的值域得到,而不能由反函数的解析式得到
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com