
4、三角函数的性质除了一般函数通性外,还出现了前面几种函数所没有的周期性。周期性的定义:设T为非零常数,若对f(x)定义域中的每一个x,均有f(x+T)=f(x),则称T为f(x)的周期。当T为f(x)周期时,kT(k∈Z,k≠0)也为f(x)周期。
三角函数图象是性质的重要组成部分。利用单位圆中的三角函数线作函数图象称为几何作图法,熟练掌握平移、伸缩、振幅等变换法则。
3、三角变换公式包括和、差、倍、半公式,诱导公式是和差公式的特例,对公式要熟练地正用、逆用、变用。如倍角公式:cos2α=2cos2α-1=1-2sin2α,变形后得 ,可以作为降幂公式使用。
,可以作为降幂公式使用。
三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备。
2、利用直角坐标系,可以把直角三角形中的三角函数推广到任意角的三角数。三角函数定义是本章重点,从它可以推出一些三角公式。重视用数学定义解题。
设P(x,y)是角α终边上任一点(与原点不重合),记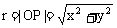 ,则
,则 ,
,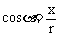 ,
, ,
,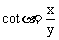 。
。
利用三角函数定义,可以得到(1)诱导公式:即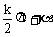 与α之间函数值关系(k∈Z),其规律是“奇变偶不变,符号看象限”;(2)同角三角函数关系式:平方关系,倒数关系,商数关系。
与α之间函数值关系(k∈Z),其规律是“奇变偶不变,符号看象限”;(2)同角三角函数关系式:平方关系,倒数关系,商数关系。
1、角的概念的推广。从运动的角度,在旋转方向及旋转圈数上引进负角及大于3600的角。这样一来,在直角坐标系中,当角的终边确定时,其大小不一定(通常把角的始边放在x轴正半轴上,角的顶点与原点重合,下同)。为了把握这些角之间的联系,引进终边相同的角的概念,凡是与终边α相同的角,都可以表示成k·3600+α的形式,特例,终边在x轴上的角集合{α|α=k·1800,k∈Z},终边在y轴上的角集合{α|α=k·1800+900,k∈Z},终边在坐标轴上的角的集合{α|α=k·900,k∈Z}。
在已知三角函数值的大小求角的大小时,通常先确定角的终边位置,然后再确定大小。
弧度制是角的度量的重要表示法,能正确地进行弧度与角度的换算,熟记特殊角的弧度制。在弧度制下,扇形弧长公式=|α|R,扇形面积公式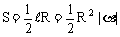 ,其中α为弧所对圆心角的弧度数。
,其中α为弧所对圆心角的弧度数。
3、三角函数的图象及性质。
2、三角公式,包括诱导公式,同角三角函数关系式和差倍半公式等;
1、三角函数的概念及象限角、弧度制等概念;
《三角函数》复习
4.(2008年上海理18)(6’+9’)
已知双曲线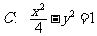 ,
,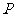 为
为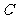 上的任意点。
上的任意点。
(1)求证:点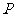 到双曲线
到双曲线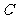 的两条渐近线的距离的乘积是一个常数;
的两条渐近线的距离的乘积是一个常数;
(2)设点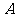 的坐标为
的坐标为 ,求
,求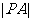 的最小值;
的最小值;
[解析](1)设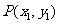 是双曲线上任意一点,
是双曲线上任意一点,
该双曲的两条渐近线方程分别是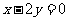 和
和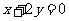 .
……2分
.
……2分
点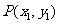 到两条渐近线的距离分别是
到两条渐近线的距离分别是 和
和 , ……4分
, ……4分
它们的乘积是
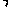
 .
.
点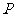 到双曲线的两条渐线的距离的乘积是一个常数.
……6分
到双曲线的两条渐线的距离的乘积是一个常数.
……6分
(2)设的坐标为 ,则
,则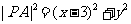 …8分
…8分
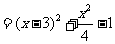
 ……11分
……11分

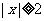 ,13分
,13分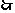 当
当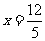 时,
时,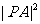 的最小值为
的最小值为 ,即
,即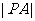 的最小值为
的最小值为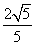 . 15分
. 15分
(Ⅱ)设直线AB的方程为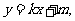 由题意知
由题意知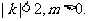
由{ 得A点的坐标为
得A点的坐标为
由{ 得B点的坐标为
得B点的坐标为 由
由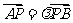 得P点的坐标为
得P点的坐标为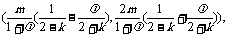 将P点坐标代入
将P点坐标代入
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m).
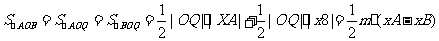
=
以下同解答一.
3.(2009年上海理21)(本题满分16分)
本题共有2个小题,第1小题满分8分,第2小题满分8分。
已知双曲线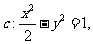 设过点
设过点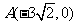 的直线l的方向向量
的直线l的方向向量


(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2)
证明:当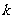 >
> 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为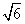 。
。
解21.(1)双曲线C的渐近线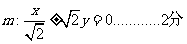
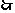 直线l的方程
直线l的方程 ………………..6分
………………..6分 

直线l与m的距离 ……….8分
……….8分 
(2)设过原点且平行与l的直线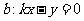
则直线l与b的距离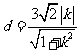 当
当


又双曲线C的渐近线为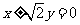

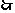 双曲线C的右支在直线b的右下方,
双曲线C的右支在直线b的右下方,
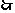 双曲线
双曲线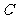 右支上的任意点到直线
右支上的任意点到直线 的距离为
的距离为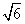 。
。
故在双曲线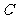 的右支上不存在点
的右支上不存在点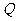 ,使之到直线
,使之到直线 的距离为
的距离为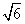 。
。
[ 证法二] 双曲线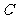 的右支上存在点
的右支上存在点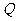
 到直线
到直线 的距离为
的距离为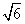 ,
,
则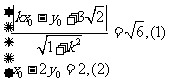 由(1)得
由(1)得 ,
, 
设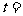
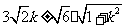

当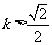 ,
,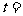
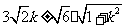
 0………………………………..13分
0………………………………..13分
将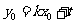 代入(2)得
代入(2)得 (*)
(*)

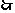 方程(*)不存在正根,即假设不成立
方程(*)不存在正根,即假设不成立 

故在双曲线C的右支上不存在Q,使之到直线l 的距离为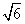 …………….16分
…………….16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com