
1.积、商、幂的对数运算法则:
如果 a > 0,a ¹ 1,M > 0, N > 0 有:

证明:①设 M=p,
M=p, 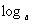 N=q. 由对数的定义可以得:M=
N=q. 由对数的定义可以得:M= ,N=
,N= .
.
∴MN= 
 =
= ∴
∴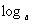 MN=p+q,
即证得
MN=p+q,
即证得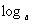 MN=
MN=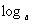 M +
M + 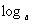 N.
N.
②设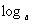 M=p,
M=p,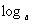 N=q. 由对数的定义可以得M=
N=q. 由对数的定义可以得M= ,N=
,N= .
.
∴ ∴
∴
 即证得
即证得 .
.
③设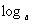 M=P
由对数定义可以得M=
M=P
由对数定义可以得M= ,
,
∴ =
= ∴
∴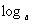
 =np, 即证得
=np, 即证得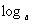
 =n
=n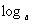 M.
M.
说明:上述证明是运用转化的思想,先通过假设,将对数式化成指数式,并利用幂的运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式.
①简易语言表达:“积的对数 = 对数的和”……
②有时逆向运用公式:如 .
.
③真数的取值范围必须是 :
:
 是不成立的.
是不成立的.
 是不成立的.
是不成立的.
④对公式容易错误记忆,要特别注意:
 ,
, .
.
4.指数运算法则 

3.重要公式:
⑴负数与零没有对数; ⑵ ,
,

⑶对数恒等式

2.指数式与对数式的互化

1.对数的定义
 其中
其中
 与
与 

2.已知 求证:
求证:
证明:由换底公式
 由等比定理得:
由等比定理得:

 ∴
∴ ∴
∴ .
.
1.证明:
证法1: 设  ,
, ,
,
则:

 ∴
∴ 从而
从而

∵
 ∴
∴ 即:
即: (获证)
(获证)
证法2: 由换底公式 左边= =右边
=右边
2.《习案》作业二十二.
以下为备用题:
换底公式及其推论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com