
3. 练习:教材第73页练习第1题.
2.对数函数的图象:
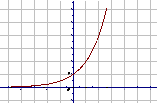
通过列表、描点、连线作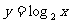 与
与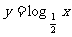 的图象:
的图象:
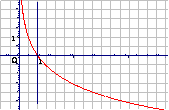
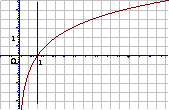
思考: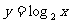 与
与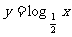 的图象有什么关系?
的图象有什么关系?
1.对数函数的定义:
函数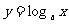
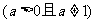 叫做对数函数,定义域为
叫做对数函数,定义域为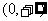 ,值域为
,值域为 .
.
例1. 求下列函数的定义域:
(1)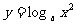 ; (2)
; (2)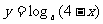 ; (3)
; (3)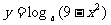 .
.
分析:此题主要利用对数函数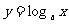 的定义域(0,+∞)求解.
的定义域(0,+∞)求解.
解:(1)由 >0得
>0得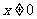 ,∴函数
,∴函数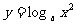 的定义域是
的定义域是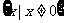 ;
;
(2)由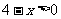 得
得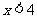 ,∴函数
,∴函数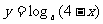 的定义域是
的定义域是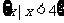 ;
;
(3)由9-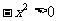 得-3
得-3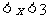 ,
,
∴函数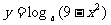 的定义域是
的定义域是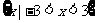 .
.
3、 我们研究指数函数时,曾经讨论过细胞分裂问题,某种细胞分裂时,得到的细胞的个数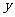 是分裂次数
是分裂次数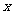 的函数,这个函数可以用指数函数
的函数,这个函数可以用指数函数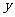 =
=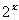 表示.
表示.
现在,我们来研究相反的问题,如果要求这种细胞经过多少次分裂,大约可以得到1万个,10万个……细胞,那么,分裂次数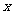 就是要得到的细胞个数
就是要得到的细胞个数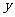 的函数.根据对数的定义,这个函数可以写成对数的形式就是
的函数.根据对数的定义,这个函数可以写成对数的形式就是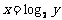 .
.
如果用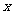 表示自变量,
表示自变量,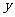 表示函数,这个函数就是
表示函数,这个函数就是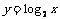 .
.
引出新课--对数函数.
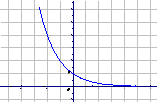
2、 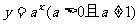 的图象和性质.
的图象和性质.
|
|
a>1 |
0<a<1 |
|
图 象 |
 |
 |
|
性 质 |
(1)定义域:R |
|
|
(2)值域:(0,+∞) |
||
|
(3)过点(0,1),即x=0时,y=1 |
||
|
(4)在 R上是增函数 |
(4)在R上是减函数 |
1、指对数互化关系:
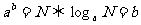
4.课堂小结
对数的运算法则,公式的逆向使用.
3.课堂练习:
教材第68页练习题1、2、3题.
2.讲授范例:
例1. 用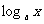 ,
,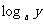 ,
,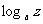 表示下列各式:
表示下列各式:
 .
.
解:(1)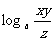 =
=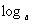 (xy)-
(xy)-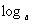 z=
z=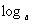 x+
x+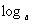 y-
y- 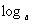 z
z
(2)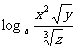 =
=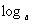 (
(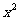
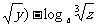
= 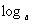
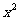 +
+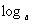
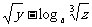 =2
=2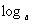 x+
x+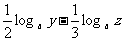 .
.
例2. 计算
(1)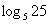 , (2)
, (2)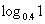 , (3)
, (3)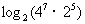 , (4)
, (4)
解:(1)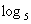 25=
25= 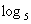
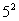 =2
=2 (2)
(2)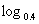 1=0.
1=0.
(3)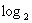 (
(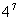 ×25)=
×25)= 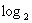
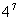 +
+ 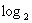
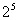 =
= 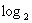
 +
+ 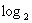
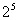 = 2×7+5=19.
= 2×7+5=19.
(4)lg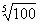 =
=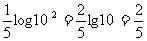 .
.
例3.计算:
(1)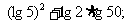 (2)
(2) 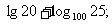
(3) 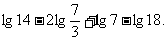
说明:此例题可讲练结合.
解:(1) 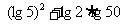 =
=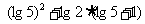 =
=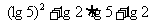
= =
= =1;
=1;
(2) 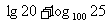 =
=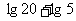 =
=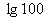 =2;
=2;
(3)解法一:lg14-2lg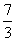 +lg7-lg18=lg(2×7)-2(lg7-lg3)+lg7-lg(
+lg7-lg18=lg(2×7)-2(lg7-lg3)+lg7-lg(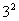 ×2)
×2)
=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0.?
解法二:
lg14-2lg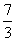 +lg7-lg18=lg14-lg
+lg7-lg18=lg14-lg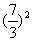 +lg7-lg18=lg
+lg7-lg18=lg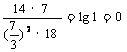
评述:此例题体现对数运算性质的综合运用,应注意掌握变形技巧,如(3)题各部分变形要化到最简形式,同时注意分子、分母的联系.(2)题要避免错用对数运算性质.
例4.已知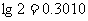 ,
,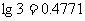 , 求
, 求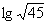
例5.课本P66面例5.
20世纪30年代,里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级M,其计算公式为
M=lgA-lgA0.
其中,A是被测地震的最大振幅,A0是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差).
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1);
(2)5级地震给人的震感已比较明显,计算7.6级地震的最大振幅是5级地震的最大振幅的多少倍(精确到1).
例6.已知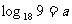 ,
,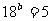 ,求
,求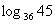 (备用题)
(备用题)
评述:此题体现了对数运算性质的灵活运用,运算性质的逆用常被学生所忽视.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com