
例1 比较下列各组数的大小;
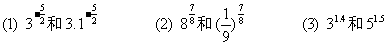
练习
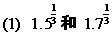
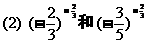
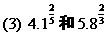
利用幂函数的增减性比较两个数的大小.
(1)若能化为同指数,则用幂函数的单调性;
(2)若能化为同底数,则用指数函数的单调性;
(3)当不能直接进行比较时,可在两个数中间插入一个中间数,间接比较上述两个数的大小
例2
证明幂函数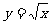 在[0,+∞)上是增函数。
在[0,+∞)上是增函数。
除了作差,还有没有其它方法呢?
4.函数y=f(x)在定义域R上是偶函数,且在(-¥,0]上是递减的,则f(x)在[0,+ ¥)上也是递减的.
3.函数y=f(x)在定义域R上是奇函数,且在(-¥,0]上是递增的,则f(x)在[0,+ ¥)上也是递增的.
2.函数f(x)=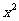 ,xÎ[-1,1)为偶函数.
,xÎ[-1,1)为偶函数.
1.函数f(x)= 为奇函数.
为奇函数.
4、幂函数的性质 : (指导学生完成78面的探究)(幻灯上的结果依此出现)
(1) 所有的幂函数在(0,+∞)都有定义,并且图象都通过点(1,1);
(2) 如果α>0,则幂函数图象过原点,并且在区间[0,+∞)上是增函数;
(3) 如果α<0,则幂函数图象在区间(0,+∞)上是减函数,
在第一象限内,当x从右边趋向于原点时,图象在y轴右方无限地逼近y轴,
当x趋向于+∞时,图象在y轴上方无限地逼近x轴;
(4) 当α为奇数时,幂函数为奇函数;当α为偶数时,幂函数为偶函数.
练一练:2、判断正误
3、在同一平面直角坐标系内作出幂函数y=x, ,
,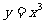 ,
,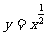 ,
,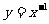 的图象:
的图象:
“正抛负双,大竖小横”,即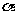 >0(
>0(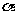 ≠1)时图象是抛物线型;
≠1)时图象是抛物线型;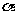 <0时图象是双曲线型;
<0时图象是双曲线型;
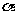 >1时图象是竖直抛物线型;0<
>1时图象是竖直抛物线型;0<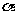 <1时图象是横卧抛物线型.
<1时图象是横卧抛物线型.
2、练一练:1。判断下列函数是否为幂函数.
(1) 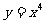 (2)
(2)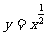 (3)
(3)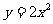 (4)
(4) (5)
(5)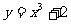
1、一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
注意:幂函数中α的可以为任意实数.
(1) 如果张红购买了每千克1元的蔬菜w千克,那么她需要支付p=w元,这里p是w的函数;
(2) 如果正方形的边长为a,那么正方形的面积S=a2,这里S是a的函数;
(3) 如果立方体的边长为a,那么立方体的体积V=a3,这里V是a的函数;
(4) 如果一个正方形场地的面积为S,那么这个正方形的边长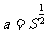 ,这里a是S的函数;
,这里a是S的函数;
(5) 如果某人t 秒内骑车行进了1 km,那么他骑车的平均速度v=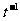 km/s,这里v是t 的函数。
km/s,这里v是t 的函数。
思考:这些函数有什么共同的特征?
他们有以下共同特点:
(1)都是函数;(2) 指数为常数. (3) 均是以自变量为底的幂;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com