
3.(2005全国Ⅰ)函数f(x)=x3+ax2+3x-9已知f(x)在x=-3时取得极值,则a=( )
A.2 B.3 C.4 D.5
2.函数y=1+3x-x3有
A.极小值-2,极大值2, B.极小值-2,极大值3
C.极小值-1,极大值1, D.极小值-1,极大值3
1.(2005广东)函数f(x)=x3-3x2+1是减函数的区间为 ( )
A.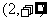 B.
B. C.
C. D.(0,2)
D.(0,2)
3.函数的最大值与最小值
(1)设y= f(x)是定义在区间[a,b]上的函数,并在(a,b)内可导,求函数在[a,b]上的最值可分两步进行:
①求y= f(x) 在(a,b)内的极值;
②将y= f(x)在各极值点的极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个为最小值。
(2)若函数f(x)在[a,b]上单调递增(或递减),则f(a)为函数的最小值(或最大值),f(b)为函数的最大值(或最小值)。
2.可导函数的极值
(1)极值的概念
设函数f(x)在点x0附近有定义,且若对x0附近所有的点都有f(x)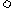 f(x0)(或f(x)
f(x0)(或f(x)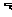 f(x0)),则称f(x0)为函数的一个极大(小)值,称x0为极大(小)值点。
f(x0)),则称f(x0)为函数的一个极大(小)值,称x0为极大(小)值点。
(2)求可导函数f(x)极值的步骤
①求导数f '(x); ②求方程f '(x)=0的根;
③检验f '(x)在方程f '(x)=0的根的左右的符号,如果根的左侧为正,右侧为负,则函数在此处取得极大值;如果在根的左侧为负,右侧为正,则函数在此处取得极小值。
1.函数的单调性
(1)函数y=f(x)在某个区间内可导,若f '(x)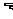 0,则f(x)为增函数;若f '(x)
0,则f(x)为增函数;若f '(x) 0,则f(x)为减函数。
0,则f(x)为减函数。
(2)求可导函数单调区间的一般步骤和方法。
①确定函数f(x)的定义区间;
②求f '(x),令f '(x)=0,解此方程,求出它在定义区间内的一切实根;
③把函数f(x)的间断点[即包括f(x)的无定义点]的横坐标和上面的各实根按由小到大的顺序排列起来,然后用这些点把函数f(x)的定义区间分成若干个小区间;
④确定f '(x)在各小区间内的符号,根据f '(x)的符号判定f(x)在每个相应小开区间内的增减性。
例如:求函数y=(x2-1)(x2-4)单调区间。
2.了解可导函数在某点处取极值的必要条件和充分条件,会求一些实际问题(单峰函数)的最大值与最小值。
1.了解可导函数的单调性与其导数的关系;
9、抽象函数(即不给出解析式,只知道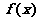 具备的条件)的研究:
具备的条件)的研究:
(1)若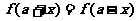 则
则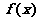 关于直线
关于直线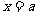 对称;
对称;
(2)若对任意的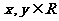 , 都有
, 都有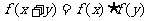 ,则
,则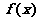 可与指数函数类比;
可与指数函数类比;
(3)若对任意的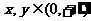 , 都有
, 都有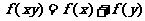 ,则
,则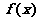 可与对数函数类比.
可与对数函数类比.
例1:设集合A和B都是坐标平面内的点集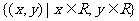 ,映射
,映射 把集合A中的元素
把集合A中的元素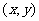 映射成集合B的元素
映射成集合B的元素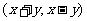 ,则在映射下象
,则在映射下象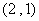 的原象是
( B ) A.
的原象是
( B ) A.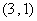 B.
B.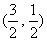 C.
C.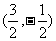 D.
D.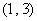
例2:设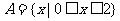 ,
,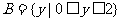 ,图中表示集合A到集合B的函数关系的图象是
( B )
,图中表示集合A到集合B的函数关系的图象是
( B )
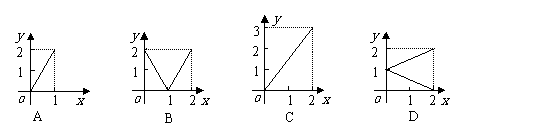
例3:函数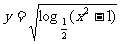 的定义域是
( A )
的定义域是
( A )
A.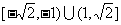 B.
B.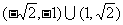 C.
C.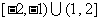 D.
D.
例4:设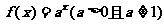 对于任意的实数x、y 都有 ( C )
对于任意的实数x、y 都有 ( C )
A.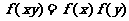 B.
B.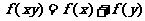
C.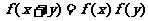 D.
D.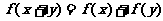
例5:方程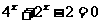 的解是
的解是
解:设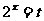 ,则
,则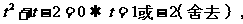 则
则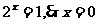
例6:方程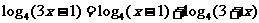 的解是
.
的解是
.
解:原方程化为
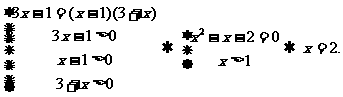
例7.若关于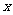 的方程
的方程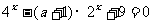 有实数根,求
有实数根,求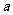 的取值范围。
的取值范围。
例8 某化工厂生产一种溶液, 按市场要求,杂质含量不能超过0.1%,若初时含杂质2%,每过滤一次可使杂质含量减少三分之一, 问至少要过滤几次才能使产品达到市场要求?
(lg2=0.3010, lg3=0.4771)
8、图象的变换规律:
①平移变换(a>0)



 a)
a)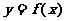
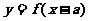 ,
,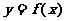
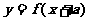 .
.
b)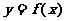
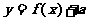 ,
,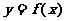
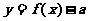 .
.
②对称翻转变换:
a)互为反函数的两个函数图象关于直线y=f(x)对称.
即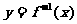 的函数图象与函数
的函数图象与函数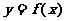 的图象关于
的图象关于 对称;
对称;
b) 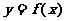 的函数图象与函数
的函数图象与函数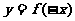 的图象关于
的图象关于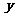 轴对称;
轴对称;
c) 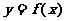 的函数图象与函数
的函数图象与函数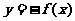 的图象关于
的图象关于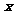 轴对称;
轴对称;
d) 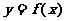 的函数图象与函数
的函数图象与函数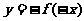 的图象关于原点对称.
的图象关于原点对称.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com