9. (2006山东)设函数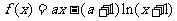，其中，求f(x)的单调区间.

解：由已知得函数f(x)的定义域为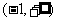，且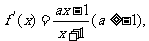

(1)当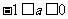时，f′(x)<0函数f(x)在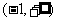上单调递减，

(2)当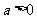时，由f′(x)=0解得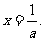

若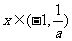，则f′(x)<0函数f(x)在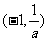上单调递减.

若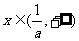则，f′(x)>0函数f(x)在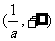上单调递增.

综上所述：

当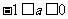时，函数f(x)在(-1,+∞)上单调递减.

当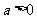时，函数f(x)在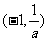上单调递减，函数f(x)在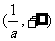上单调递增.

8. (2005北京)

已知函数f(x)= －x³+3x²+9x+a

(Ⅰ)求f(x)的单调减区间；

(Ⅱ)若f(x)在区间[－2，2].上的最大值为20，求它在该区间上的最小值.

解：(I)f′(x)= －3x²+6x+9 令f′(x)<0，解得x<－1或x>3

所以函数f(x)的单调递减区间为(－∞,－1),(3,+∞)

(II)因为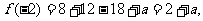

所以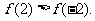

因为在(－1，3)上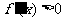，所以f(x)在[－1，2]上单调递增，又由于f(x)在

[－2，－1]上单调递减，因此f(2)和f(-1)分别是f(x)在区间[－2，2]上的最大值和

最小值.

于是有22+a=20，解得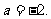a=－2

故f(x)= －x³+3x²+9x－2　 因此f(－1)=1+3－9－2=－7

即函数f(x)在区间[－2，2]上的最小值为－7.

7.(2006北京)

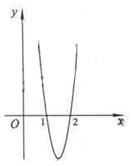
已知函数f(x)=ax³+bx²+cx在点x₀处取得极大值5，其导函数y=f′(x)的图象经过点(0,1)，(2,0)，如图所示.求：

(Ⅰ)x₀的值；

(Ⅱ)a,b,c的值.

解法一：

(Ⅰ)由图像可知，在(－∞,1)上f′(x)>0，在(1,2)上f′(x)<0，在(2,+∞)上f′(x)>0

故f(x)在(－∞,1), (2,+∞)上递增，在(1,2)　　 上递减，

因此f(x)在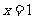处取得极大值，所以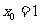

(Ⅱ)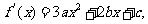

由f′(1)=0, f′(2)=0, f(1)=5

得

解得a=2, b= -9, c=12.

解法二：

(Ⅰ)同解法一

(Ⅱ)设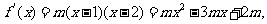

又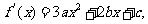

所以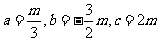

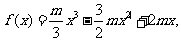
由f(1)=5,即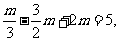得m=6

所以a=2,b=－9,c=12

5. (0,2)；6. 最大值是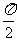，最小值是-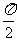

[解答题]

3. 解析：F(x)=f［g(x)］=x⁴－4x²+6，(x)=4x³－8x，

令(x)>0，得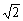－<x<0或x>，

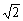∴F(x)在(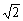－，0)上递增

1. (x)=3x²－a在［1，+∞)上，(x)≥0恒成立，即a≤3x²在［1，+∞)上恒成立，∴a≤3.

6.函数f(x)=sin2x-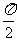x,(-≤x≤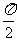)的最大值是　　　　 ，最小值是　　　　 。

简答提示：1－4：DACC ；

5.函数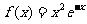的单调增区间是　　　　　

4.函数y=xsinx+cosx在下面哪个区间内是增函数

A.(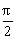,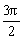)　　　　　　　　　　　　 B.(π,2π)

C.(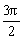, 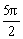)　　　　　　　　　　　 D.(2π,3π)

[填空题]

2.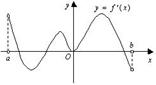(2006天津)函数f(x)的定义域为开区间(a,b)，导函数f′(x)在(a,b)内的图象如图所示，则函数f(x)在开区间(a,b)内有极小值点(　 )

A．1个 　　　　　　　 B．2个

C．3个　　　　　　　　 D． 4个

3已知f(x)=(x－1)²+2，g(x)=x²－1，则f［g(x)］

A.在(－2，0)上递增　　 B.在(0，2)上递增

C.在(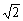－，0)上递增　 D.在(0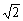，)上递增