
78、(湖南省长沙市一中2008届高三第六次月考)数列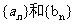 ,由下列条件确定:①a1<0,b1<0.②当k≥2时,ak和bk满足下列条件:当
,由下列条件确定:①a1<0,b1<0.②当k≥2时,ak和bk满足下列条件:当 .
.
(1)若 ,
,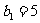 ,分别写出{an}、{bn}的前四项.
,分别写出{an}、{bn}的前四项.
(2)证明数列{ak-bk}是等比数列.
(3)设 是满足b1>b2>…>bn的最大整数时,用a1、b1表示n满足的条件.
是满足b1>b2>…>bn的最大整数时,用a1、b1表示n满足的条件.
解:(1)
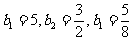 ………………………………………………………………………(3分)
………………………………………………………………………(3分)
(2)当 时,
时,
当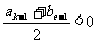 时,
时,
又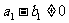 ,∴数列
,∴数列 是等比数列. ……………………………………………(9分)
是等比数列. ……………………………………………(9分)
(3)当b1>b2>…>bn(n≥2)时,bk≠bk-1(2≤k≤n).
由(2)知: 不成立,
不成立,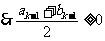 .
.
从而对于2≤k≤n有ak=ak-1,bk=
于是 ……………………………………………………………………(11分)
……………………………………………………………………(11分)

若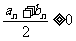 ,则
,则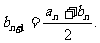
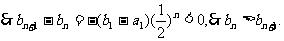
这与 是满足b1>b2>…>bn(n≥2)的最大整数矛盾.
是满足b1>b2>…>bn(n≥2)的最大整数矛盾.
∴n是满足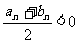 的最小整数.
的最小整数.

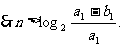
 n是满足大于
n是满足大于 的最小整数.…………………………(13分)
的最小整数.…………………………(13分)
77、(湖南省十二校2008届高三第一次联考)已知二次函数 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为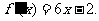 数列{
数列{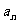 }的前n项和为
}的前n项和为 ,点
,点 均在函数
均在函数 的图像上.
的图像上.
(I)求数列{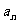 }的通项公式;
}的通项公式;
(II)设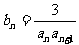 ,
,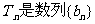 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m.
都成立的最小正整数m.
解:(I)设这二次函数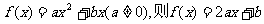 ,
,
由于 ,得
,得
 …………2分
…………2分
又因为点 的图像上,
的图像上,
所以
当
 …………6分
…………6分
(II)由(I)得知
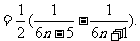 …………7分
…………7分
故
 …………9分
…………9分
因此,要使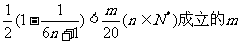 ,必须且仅须满足
,必须且仅须满足
即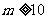 , …………11分
, …………11分
所以满足要求的最小正整数m为10。 …………12分
76、(湖北省武汉市武昌区2008届高中毕业生元月调研测试)设不等式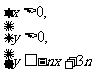 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的格点(
内的格点(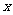 ,
,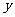 )(
)(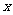 、
、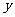 ∈z)的个数为
∈z)的个数为 (
( ∈
∈ ).
).
(Ⅰ) 求 ,
,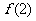 的值及
的值及 的表达式;
的表达式;
(Ⅱ)记 ,若对于任意
,若对于任意 ∈
∈ ,总有
,总有 ≤m成立,求实数m的取值范围;
≤m成立,求实数m的取值范围;
(Ⅲ) 设 为数列{
为数列{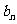 }的前
}的前 项和,其中
项和,其中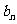 =
=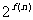 ,问是否存在正整数
,问是否存在正整数 、t,使
、t,使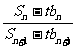 <
< 成立?若存在,求出正整数
成立?若存在,求出正整数 ,t;若不存在,请说明理由.
,t;若不存在,请说明理由.
解:(Ⅰ) =3,
=3,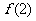 =6.
………………………………………2分
=6.
………………………………………2分
由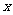 >0,0<
>0,0<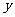 ≤
≤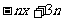 ,得0<
,得0<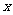 <3,又
<3,又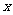 ∈
∈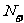 ,∴
,∴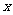 =1,或
=1,或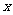 =2.
=2.
当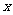 =1,0<
=1,0<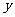 ≤2
≤2 时,共有2
时,共有2 个格点;
个格点;
当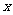 =2,0<
=2,0<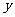 ≤
≤ 时,共有
时,共有 个格点.
个格点.
故 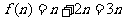 . ………………………………………………………4分
. ………………………………………………………4分
(Ⅱ)由(1)知 =
=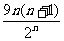 ,则
,则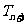 -
- =
=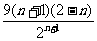 .
.
∴当 ≥3时,
≥3时,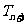 <
< .
.
又 =9<
=9< =
=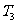 =
=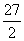 ,所以
,所以 ≤
≤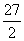 ,故
,故 ≥
≥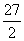 . ………………………8分
. ………………………8分
(Ⅲ)假设存在满足题意的 和
和 ,
,
由(1)知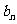 =
=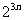 =
= ,故
,故 . ……………………………10分
. ……………………………10分
则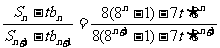 <
< .
.
变形得 <
< ,即
,即 <0.
<0.
∴1< (8-
(8-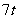 )<15.
)<15.
由于 、
、 均为正整数,所以
均为正整数,所以 =
= =1.
…………………………………14分
=1.
…………………………………14分
附: ,
,  .
.
当 时, 由
时, 由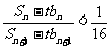 ,得
,得 ,
,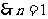 .
.
当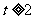 时,
时,  ,由
,由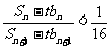 ,得
,得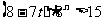 ,
, 不存在.
不存在.
所以 =
= =1.
=1.
75、(湖北省随州市2008年高三五月模拟)已知函数
⑴求
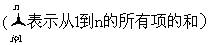
⑵若数列 满足
满足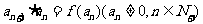 ,试求
,试求 的值,使得数列
的值,使得数列 成等差数列。
成等差数列。


74、(湖北省荆州市2008届高中毕业班质量检测)已知数列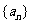 为等差数列,
为等差数列, ,且其前
,且其前 项和为
项和为 ,又正项数列
,又正项数列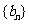 满足
满足
⑴求数列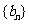 的通项公式;
的通项公式;
⑵比较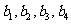 的大小;
的大小;
⑶求数列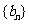 的最大项;
的最大项;
⑷令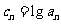 ,数列
,数列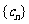 是等比数列吗?说明理由。
是等比数列吗?说明理由。
解:⑴设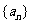 的公差为
的公差为 ,则
,则
且 ,得
,得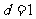 ,从而
,从而
故 (3分)
(3分)
⑵

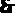
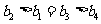 (6分)
(6分)
⑶由(2)猜想 递减,即猜想当
递减,即猜想当 ≥
≥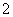 时,
时,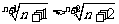 (8分)
(8分)
考察函数 ,当
,当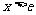 时
时

故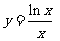 在
在 上是减函数,而
上是减函数,而 ≥
≥
所以 ,即
,即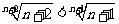
于是猜想正确,因此,数列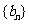 的最大项是
的最大项是 (10分)
(10分)
⑷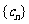 不是等比数列
不是等比数列
由 知
知
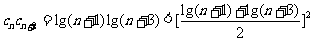

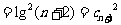
故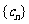 不是等比数列.
不是等比数列.
73、(湖北省荆门市2008届上期末)设数列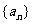 的前n项和为Sn=2n2,
的前n项和为Sn=2n2, 为等比数列,且
为等比数列,且
(1)求数列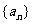 和
和 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列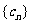 的前n项和
的前n项和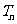 。
。
解:(1):当

故{an}的通项公式为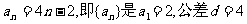 的等差数列.
的等差数列.
设{bn}的通项公式为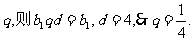
故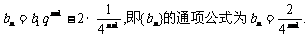 ……………6分
……………6分
(2)
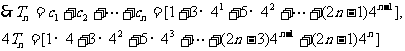
两式相减得
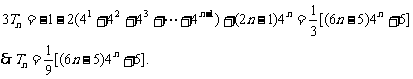
72、(湖北省荆门市2008届上期末)已知 ,且
,且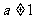 ,数列
,数列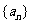 的前
的前 项和为
项和为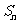 ,它满足条件
,它满足条件 .数列
.数列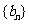 中,
中,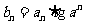 。
。
(1)求数列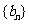 的前
的前 项和
项和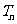 ;
;
(2)若对一切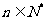 都有
都有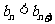 ,求
,求 的取值范围。
的取值范围。
解:(1)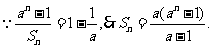
当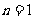 时,
时,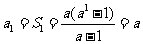 . …………2分
. …………2分
当 ≥2时,
≥2时, =
=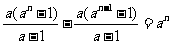 ,
,

 …………4分
…………4分
此时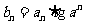
 ·
·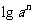 =
= ·
· ,
,

 ……
……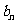 =
= …………6分
…………6分
设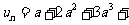 ……+
……+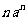 ,
,

 ……+
……+
 ,
,

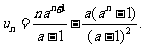

 …………8分
…………8分
(2)由 可得
可得
 当
当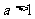 时,由
时,由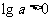 可得
可得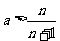 ,
,

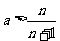 对一切
对一切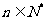 都成立,
都成立, 此时的解为
此时的解为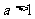 . …………10分
. …………10分
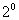 当
当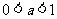 时,由
时,由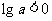 可得
可得

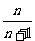 ≥
≥

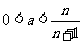 对一切
对一切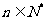 都成立,
都成立,
 此时的解为
此时的解为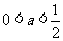 . …………12分
. …………12分
由 ,
,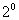 可知,对一切
可知,对一切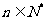 都有
都有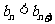 的
的 的取值范围是
的取值范围是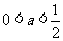 或
或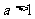 .
.
71、(湖北省黄冈市2007年秋季高三年级期末考试)已知各项均为正数的数列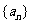 满足
满足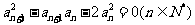 且
且 是
是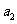 、
、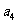 的等差中项
的等差中项
(1)求数列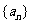 的通项公式
的通项公式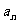 ;
;
(2)若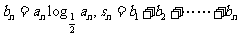 ,求使
,求使 成立的正整数
成立的正整数 的最小值。
的最小值。
解: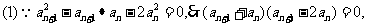
 数列
数列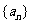 的各项均为正数,
的各项均为正数,
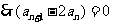 ,
,
即
 数列
数列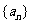 是以2为公比的等比数列。
是以2为公比的等比数列。

 是
是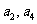 的等差中项,
的等差中项,

 数列
数列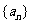 的通项公式为
的通项公式为
(2)由(1)及 ,得
,得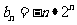 ,(6分)
,(6分)
 ①
①
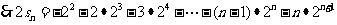 ②
②
②-①得,
要使 成立,只需
成立,只需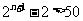 成立,即
成立,即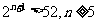
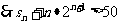 成立的正整数n的最小值为5。(12分)
成立的正整数n的最小值为5。(12分)
70、(湖北省黄冈市麻城博达学校2008届三月综合测试)把正奇数数列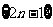 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第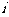 行,从左往右数第
行,从左往右数第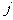 个数。
个数。
(Ⅰ)若 ,求
,求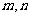 的值;
的值;
(Ⅱ)已知函数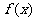 的反函数
的反函数 为,若记三角形数表中从上往下数第
为,若记三角形数表中从上往下数第 行各数的和为
行各数的和为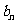 ,求数列
,求数列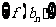 的前
的前 项和
项和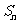 。
。
解:(Ⅰ)∵三角形数表中前 行共有
行共有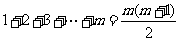 个数,
个数,
∴第 行最后一个数应当是所给奇数列中第
行最后一个数应当是所给奇数列中第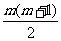 项,即
项,即 。
。
因此,使得 的
的 是不等式
是不等式 的最小正整数解。
的最小正整数解。
由 得
得 ,∴
,∴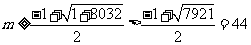 。∴
。∴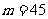 。
。
第45行第一个数是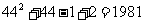 ,∴
,∴
(Ⅱ)∵ ,∴
,∴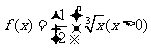 。
。
∵第 行最后一个数是
行最后一个数是 ,且有
,且有 个数,若
个数,若 将看成第
将看成第 行第一个数,则第
行第一个数,则第 行各数成公差为
行各数成公差为 的等差数列,故
的等差数列,故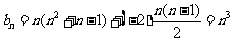 。∴
。∴ 。
。
故 。用错位相减法可求得
。用错位相减法可求得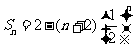 。
。
69、(湖北省鄂州市2008年高考模拟)已知函数 的图象按向量
的图象按向量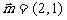 平移后便得到函数
平移后便得到函数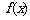 的图象,数列
的图象,数列 满足
满足 (n≥2,nÎN*).
(n≥2,nÎN*).
(Ⅰ)若 ,数列
,数列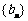 满足
满足 ,求证:数列
,求证:数列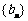 是等差数列;
是等差数列;
(Ⅱ)若 ,数列
,数列 中是否存在最大项与最小项,若存在,求出最大项与最小项,若不存在,说明理由;
中是否存在最大项与最小项,若存在,求出最大项与最小项,若不存在,说明理由;
(Ⅲ)若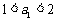 ,试证明:
,试证明: .
.
解: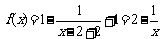 ,则
,则 (n≥2,nÎN*).
(n≥2,nÎN*).
(Ⅰ) ,
, ,∴
,∴ (n≥2,nÎN*).∴数列
(n≥2,nÎN*).∴数列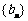 是等差数列.
是等差数列.
(Ⅱ)由(Ⅰ)知,数列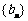 是等差数列,首项
是等差数列,首项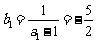 ,公差为1,则其通项公式
,公差为1,则其通项公式 ,
,
由 得
得 ,故
,故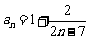 .
.
构造函数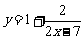 ,则
,则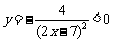 .函数
.函数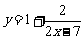 在区间
在区间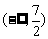 ,
, 上为减函数.
上为减函数.
∴当 时,
时, ,且在
,且在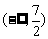 上递减,故当
上递减,故当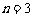 时,
时,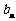 取最小值
取最小值 ;当
;当 时,
时, ,且在
,且在 上递减,故当
上递减,故当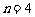 时,
时,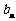 取最大值
取最大值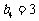 .故存在.
.故存在.
(Ⅲ)先用数学归纳法证明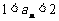 ,再证明
,再证明 .
.
①当n=1时,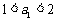 成立,
成立,
②假设n=k时命题成立,即 ,
,
则当n=k+1时,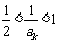 ,
,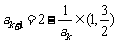 ,则
,则 ,故当n=k+1时也成立.
,故当n=k+1时也成立.
综合①②有,命题对任意nÎN*时成立,即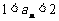 .下证
.下证 .
.
∵ ,∴
,∴ .综上所述:
.综上所述: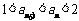 .
.
[总结点评]本题集数列、向量、函数、导数、不等式于一体,充分展示了《考试大纲》“构造有一定深度和广度的数学问题,要注重问题的多样化,体现思维的发散性”的题目,这需要我们加强这一方面的训练,需要从多层次、多角度去思考问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com