
7、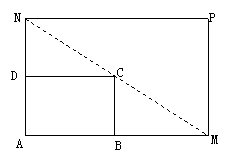 (广东省揭阳市2008年高中毕业班高考调研测试)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(广东省揭阳市2008年高中毕业班高考调研测试)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(1) 要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)
若|AN| 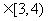 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
解:设AN的长为x米(x >2)
∵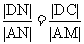 ,∴|AM|=
,∴|AM|=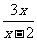
∴SAMPN=|AN|•|AM|=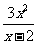 ------------------------------------- 4分
------------------------------------- 4分
(1)由SAMPN > 32 得
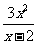 > 32 ,
> 32 ,
∵x >2,∴ ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴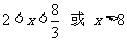 即AN长的取值范围是
即AN长的取值范围是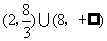 ----------- 8分
----------- 8分
(2)令y=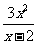 ,则y′=
,则y′=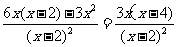 -------------- 10分
-------------- 10分
∵当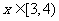 ,y′< 0,∴函数y=
,y′< 0,∴函数y=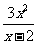 在
在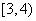 上为单调递减函数,
上为单调递减函数,
∴当x=3时y=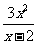 取得最大值,即
取得最大值,即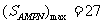 (平方米)
(平方米)
此时|AN|=3米,|AM|=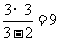 米
米
6、(福建省厦门市2008学年高三质量检查)某化工集团在靠近某河流修建两个化工厂,流
 经第一化工厂的河流流量为500万立方米/天,在两
经第一化工厂的河流流量为500万立方米/天,在两
个化工厂之间还有一条流量为200万立方米/天的支
流并入大河(如图)。第一化工厂每天排放含有某种
有害物质的工业废水2万立方米;第二化工厂每天
排放这种工业废水1.4万立方米,从第一化工厂排出
的工业废水在流到第二化工厂之前,有20%可自然
净化。
环保要求:河流中工业废水的含量应不大于0.2%,
因此,这两个工厂都需各自处理部分的工业废水,第
一化工厂处理工业废水的成本是1000元/万立方米,
第二化工厂处理工业废水的成本是800元/万立方米。
试问:在满足环保要求的条件下,两个化工厂应各自
处理多少工业废水,才能使这两个工厂总的工业废水
处理费用最小?
解:设第一化工厂每天处理工业废水x万立方米,
需满足: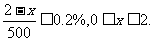 …………2分
…………2分
设第二化工厂每天处理工业废水y万立方米,
需满足: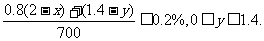 …………4分
…………4分
两个化工厂每天处理工业废水总的费用为1000x+800y元。
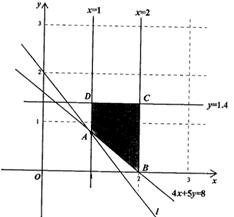 问题即为:在约束条件
问题即为:在约束条件

求目标函数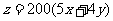 的最小值。
的最小值。
5、(山东省博兴二中高三第三次月考)为了立一块广告牌,要制造一个三角形的支架. 三角形支架形状如图,要求 ,BC的长度大于1米,且AC比AB长0.5米. 为了广告牌稳固,要求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
,BC的长度大于1米,且AC比AB长0.5米. 为了广告牌稳固,要求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
解:如图,设BC的长度为x米,AC的长度为y米,则AB的长度
为(y-0.5)米. 在△ABC中,依余弦定理得:
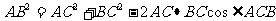 -------(4分)
-------(4分)
即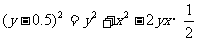
化简,得
∵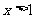 ,∴
,∴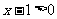 因此
因此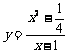 ------------------(6分)
------------------(6分)
方法一: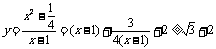 .
-------------------- (10分)
.
-------------------- (10分)
当且仅当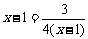 时,取“=”号,即
时,取“=”号,即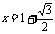 时,y有最小值
时,y有最小值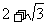 .
.
方法二: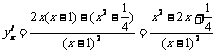 -----------------(9分)
-----------------(9分)
解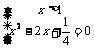 ,得
,得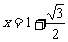 ------------------------(11分)
------------------------(11分)
∵当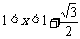 时,
时,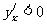 ;当
;当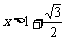 时,
时,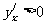 .
.
∴当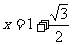 时,y有最小值
时,y有最小值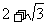 .
.
18.①由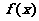 是R上的奇函数,
是R上的奇函数,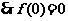 ,又因
,又因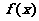 是R上的单调函数,
是R上的单调函数,
由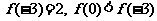 ,所以
,所以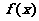 为R上的减函数。
为R上的减函数。
②当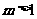 时,
时, ;
;
当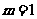 时,
时,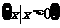
当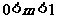 时,
时,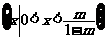 。
。
4、(四川省乐山市2008届第一次调研考试)已知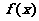 是R上的单调函数,且对任意的实数
是R上的单调函数,且对任意的实数 ,有
,有 恒成立,若
恒成立,若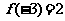
①求证: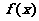 是R上的减函数;②解关于
是R上的减函数;②解关于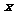 的不等式:
的不等式:
解:①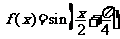 ;②
;②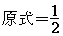 ;
;
3、(四川省巴蜀联盟2008届高三年级第二次联考)如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
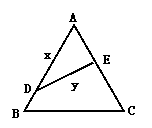 (2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
解:(1)在△ADE中,y2=x2+AE2-2x·AE·cos60° y2=x2+AE2-x·AE,①
y2=x2+AE2-x·AE,①
又S△ADE=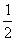 S△ABC=
S△ABC=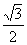 a2=
a2=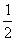 x·AE·sin60°
x·AE·sin60° x·AE=2.②
x·AE=2.②
②代入①得y2=x2+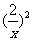 -2(y>0), ∴y=
-2(y>0), ∴y=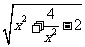 (1≤x≤2).
(1≤x≤2).
(2)如果DE是水管y= ≥
≥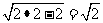 ,
,
当且仅当x2=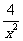 ,即x=
,即x=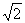 时“=”成立,故DE∥BC,且DE=
时“=”成立,故DE∥BC,且DE=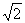 .
.
如果DE是参观线路,记f(x)=x2+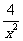 ,可知
,可知
函数在[1,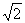 ]上递减,在[
]上递减,在[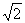 ,2]上递增,
,2]上递增,
故f(x) max=f(1)=f(2)=5. ∴y max=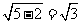 .
.
即DE为AB中线或AC中线时,DE最长.
2、(江苏省启东中学高三综合测试四)某公司一年需要一种计算机元件8000个,每天需同样多的元件用于组装整机,该元件每年分n次进货,每次购买元件的数量均为x,购一次货需手续费500元.已购进而未使用的元件要付库存费,假设平均库存量为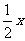 件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
件,每个元件的库存费为每年2元,如果不计其他费用,请你帮公司计算,每年进货几次花费最小?
解:设购进8000个元件的总费用为S,一年总库存费用为E,手续费为H.
则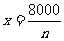 ,
,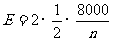 ,
,
所以S=E+H=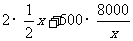
=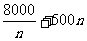
=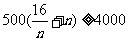 \
\
当且仅当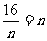 ,即n=4时总费用最少,故以每年进货4次为宜.\
,即n=4时总费用最少,故以每年进货4次为宜.\
1、(江苏省启东中学2008年高三综合测试一)关于实数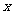 的不等式
的不等式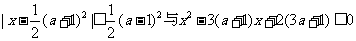 的解集依次为
的解集依次为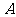 与
与 ,求使
,求使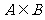 的
的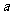 的取值范围。
的取值范围。
解:由
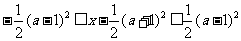
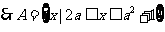
由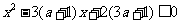 得
得
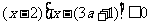
当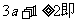
 时得
时得
当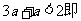
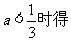
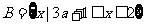
综上解述:当 时若
时若 则
则

解得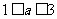
当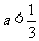 时若
时若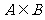 则
则

解得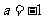
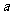 的范围是
的范围是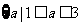 或
或
35、
34、(山西大学附中2008届二月月考)不等式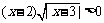 的解集为________________.
的解集为________________.
答案:(2,3)∪(3,+∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com