
17、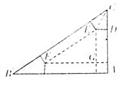 (湖南省长沙市一中2008届高三第六次月考)某加工厂有一块三角形的铁板余料(如图),经测量得知:AC=3,AB=3
(湖南省长沙市一中2008届高三第六次月考)某加工厂有一块三角形的铁板余料(如图),经测量得知:AC=3,AB=3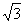 ,BC=6.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算容器的高为多少时,容器的容积最大?最大容积是多少?
,BC=6.工人师傅计划用它加工成一个无盖直三棱柱型水箱,设计方案为:将图中的阴影部分切去,再把它沿虚线折起,请计算容器的高为多少时,容器的容积最大?最大容积是多少?
解:设容器的高为x.
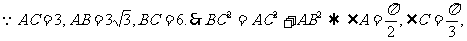
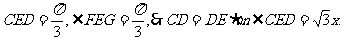
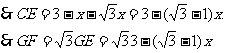
又GE>0,∴0<x<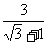
设容器的容积为V.
则V= …………………………………………………………(6分)
…………………………………………………………(6分)
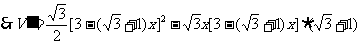
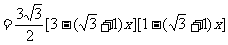 ……………………………………………………(7分)
……………………………………………………(7分)
令 ,又0<x<
,又0<x<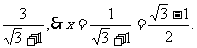 ………………………………(10分)
………………………………(10分)
当0<x<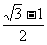 时,
时,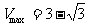 .………………………………………(13分)
.………………………………………(13分)
16、(湖北省黄冈中学2008届高三第一次模拟考试)随着机构改革的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数),每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的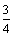 . 为获得最大的经济效益,该公司应裁员多少人?
. 为获得最大的经济效益,该公司应裁员多少人?
解:设裁员x人,可获得的经济效益为y万元,
则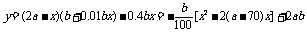 ……4分
……4分
依题意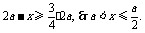
又140<2a<420, 70<a<210. ……6分
(1)当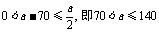 时,x=a-70, y取到最大值;……8分
时,x=a-70, y取到最大值;……8分
(2)当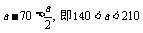 时,
时,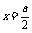 ,
y取到最大值;……10分
,
y取到最大值;……10分
答:当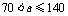 时,裁员a-70人;当
时,裁员a-70人;当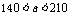 时,裁员
时,裁员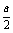 人……12分
人……12分
15、(湖北省鄂州市2008年高考模拟)某工厂有一个容量为300吨的水塔,每天从早上6时起到晚上10时止供应该厂的生产和生活用水,已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间t(小时,且规定早上6时t=0)的函数关系为W=100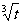 .水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
.水塔的进水量分为10级,第一级每小时进水10吨,以后每提高一级,每小时进水量就增加10吨.若某天水塔原有水100吨,在开始供水的同时打开进水管,问进水量选择为第几级时,既能保证该厂的用水(水塔中水不空)又不会使水溢出?
解:设进水量选第x级,则t小时后水塔中水的剩余量为:
y=100+10xt-10t-100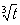 ,且0≤t≤16.
,且0≤t≤16.
根据题意0<y≤300,∴0<100+10xt-10t-100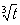 ≤300.
≤300.
当t=0时,结论成立.
当t>0时,由左边得x>1+10( ), 令m=
), 令m=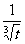 ,由0<t≤16,m ≥
,由0<t≤16,m ≥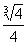 ,
,
记f(t)=1+10( )=1+10m2-10m3,(m ≥
)=1+10m2-10m3,(m ≥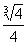 )
)
则f¢(t)=20m – 30 m 2 =0得m = 0或m =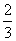 .
.
∵当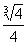 ≤m <
≤m <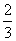 时,f¢(t)>0;当m >
时,f¢(t)>0;当m >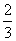 时,f¢(t)<0,
时,f¢(t)<0,
∴所以m =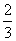 时(此时t =
时(此时t =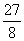 ),f(t)最大值=1+10(
),f(t)最大值=1+10(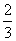 )2-10(
)2-10(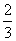 )3=
)3=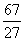 ≈2.48.
≈2.48.
当t=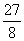 时,1+10(
时,1+10( )有最大值2.48.
)有最大值2.48.
∴x>2.48,即x≥3.
由右边得x≤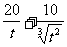 +1,当t=16时,
+1,当t=16时,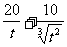 +1有最小值
+1有最小值
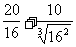 +1=
+1=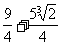 ∈(3,4).即x≤3.
∈(3,4).即x≤3.
综合上述,进水量应选为第3级.
[总结点评]本题考查数学建模的基本思想,怎么样把实际问题转化为数学问题,进而用已有的数学知识求这个数学问题的解。水塔中的水不空又不会使水溢出等到价于进出水量的平衡,进水量与选择的进水级别与进水时间相关,出水量有生活用水与工业用水两部分构成,故水塔中水的存量是一个关于进水级别与用水时间的函数,而容量为300吨的水塔就构成一个不等式,解之得问题的解.
14、(湖北省三校联合体高2008届2月测试)随着机构改革的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数 ,每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
,每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的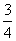 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
解:设裁员x人,可获得的经济效益为y万元,则
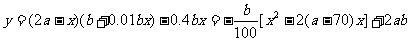 ……………4分
……………4分
依题意
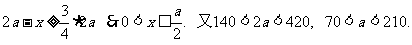 ……………6分
……………6分
(1)当 取到最大值;……………8分
取到最大值;……………8分
(2)当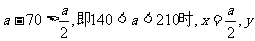 取到最大值;……………10分
取到最大值;……………10分
答:当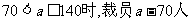 ,
,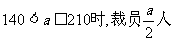 ……………12分
……………12分
13、(湖北省八校高2008第二次联考)两家共同拥有一块土地 ,形状是等腰直角三角形,
,形状是等腰直角三角形, ,
,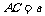 m,如果两家人准备划分一条分割线(直线段),使两家所得土地相等,其中
m,如果两家人准备划分一条分割线(直线段),使两家所得土地相等,其中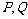 分别在线段
分别在线段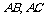 上.
上.
(Ⅰ)如果准备在分割线上建造一堵墙,请问如何划分割线,才能使造墙费用最少;
(Ⅱ)如果准备在分割线上栽种同一种果树,请问如何划分割线,才能使果树的产量最大.
解:设AQ=x,AP=y, 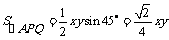 ,又
,又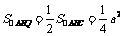 ,
,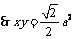 .
.
PQ=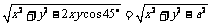 .
.
(1)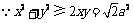 ,
, 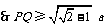 ,此时
,此时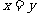 ,又
,又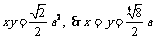 .
.
即取AP=AQ=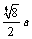 m时,PQ的长最短,因而造墙费用最少.
…………(6分)
m时,PQ的长最短,因而造墙费用最少.
…………(6分)
(2)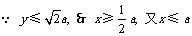 ,
,
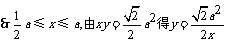 .
.
考察函数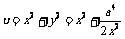 ,得当
,得当 时,函数递增,当
时,函数递增,当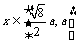 时,函数递减, 所以函数的最大值
时,函数递减, 所以函数的最大值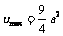 ,此时
,此时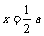 .
.
故当P取在B点,Q取在AC的中点处时,PQ最长,因而果树的产量最大. ……(12分)
12、(黑龙江省哈尔滨三中2008年高三上期末)某小型自来水厂的蓄水池中存有400吨水,水厂每小时可向蓄水池中注入自来水60吨,若蓄水池向居民不断的供水,且t小时内供水总量为210·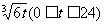 吨。
吨。
(1)供水开始几小时后,蓄水池中的水量为最小?最小水量为多少吨?
(2)若蓄水池中的水量小于200吨,就会出现供水紧张问题,试问在一天的24小时内,有多少小时会出现供水紧张情况?
答案:(1) 小时,400-140
小时,400-140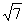 吨
吨
(2)10.5小时
11、为贯彻落实党的十七大精神,加快新农村建设步伐,红星镇政府投资c万元生产甲乙两种商品,据测算,投资甲商品x万元,可获得利润P=x万元,投资乙商品x万元可获得利润Q=40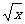 万元,如果镇政府聘请你当投资顾问,试问对甲乙两种商品的资金投入分别是多少万元?才能获得最大利润,获得最大利润是多少万元?
万元,如果镇政府聘请你当投资顾问,试问对甲乙两种商品的资金投入分别是多少万元?才能获得最大利润,获得最大利润是多少万元?
解:设对甲厂投入x万元(0≤x≤c),则对乙厂投入为c-x万元.所得利润为
y=x+40 (0≤x≤c) ……………………(3分)
(0≤x≤c) ……………………(3分)
令 =t(0≤t≤
=t(0≤t≤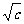 ),则x=c-t2
),则x=c-t2
∴y=f(t)=-t2+40t+c=-(t-20)2+c+400……………………(6分)
当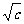 ≥20,即c≥400时,则t=20, 即x=c-400时, ymax =c+400… (8分)
≥20,即c≥400时,则t=20, 即x=c-400时, ymax =c+400… (8分)
当0<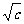 <20,
即0<c<400时,则t=
<20,
即0<c<400时,则t=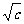 ,即x=0时,ymax=40
,即x=0时,ymax=40 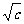 .…(10分)
.…(10分)
答:若政府投资c不少于400万元时,应对甲投入c-400万元, 乙对投入400万元,可获得最大利润c+400万元.政府投资c小于400万元时,应对甲不投入,的把全部资金c都投入乙商品可获得最大利润40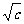 万元.…(12分)
万元.…(12分)
10、设有关于x的不等式
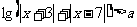
(1)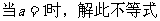
(2)当a为何值时,此不等式的解集为R(本题满分12分)
解: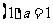 时,不等式可化为
时,不等式可化为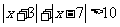 …………………………… 2分
…………………………… 2分
由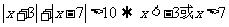 ……………………………………………..4分
……………………………………………..4分
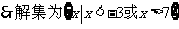 …………………………………………………………5分
…………………………………………………………5分
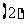
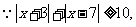 …………………………………………………………….7分
…………………………………………………………….7分
欲使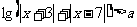 恒成立,即
恒成立,即 恒成立,
恒成立,
只须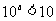 即可
即可
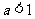 ……………………………………………………….. 10分
……………………………………………………….. 10分
9、(河北衡水中学2008年第四次调考)已知函数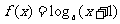 ,点
,点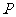 是函数
是函数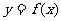 图像上任意一点,点
图像上任意一点,点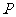 关于原点的对称点
关于原点的对称点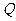 的轨迹是函数
的轨迹是函数 的图像
的图像
(1)当 时,解关于
时,解关于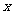 的不等式
的不等式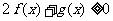 ;
;
(2)当 ,且
,且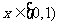 时,总有
时,总有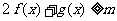 恒成立,求
恒成立,求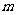 的取值范围.
的取值范围.
解:由题意知:P、Q关于原点对称,设Q(x,y)是函数y=g(x)图像上任一点,则P(-x,-y)是f(x)=loga(x+1)上的点,所以-y=loga(-x+1),于是g(x)=-loga(1-x).
(1)0<a<1,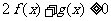
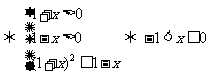
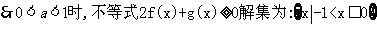
(2)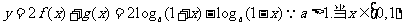 时
时
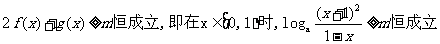

设

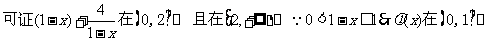
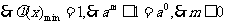
8、(广东省深圳外国语学校2008届第三次质检)据调查,某地区100万从事传统农业的农民,人均收入3000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有x(x>0)万人进企业工作,那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3000a元(a>0)。
(I)在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入,试求x的取值范围;
(II)在(I)的条件下,当地政府应该如何引导农民(即x多大时),能使这100万农民的人均年收入达到最大。
解:(I)由题意得(100-x)·3000·(1+2x%)≥100×3000,
即x2-50x≤0,解得0≤x≤50, ……………………4分
又∵x>0 ∴0<x≤50; ……………………6分
(II)设这100万农民的人均年收入为y元,
则y= =
=-[x-25(a+1)]2+3000+475(a+1)2 (0<x≤50) ………………9分
(i)当0<25(a+1)≤50,即0<a≤1,当x=25(a+1)时,y最大; ………………11分
(ii)当25(a+1)>50,即a >1,函数y在(0,50]单调递增,∴当x=50时,y取最大值。…………13分
答:在0<a≤1时,安排25(a +1)万人进入企业工作,在a>1时安排50万人进入企业工作,才能使这100万人的人均年收入最大 ………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com