
3、(江苏省南京市2008届高三第一次调研测试)已知:以点C (t, )(t∈R , t ≠ 0)为圆心的圆与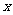 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.
解:(1) ,
,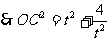 .
.
设圆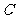 的方程是
的方程是 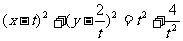 …………2分
…………2分
令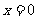 ,得
,得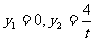 ;令
;令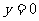 ,得
,得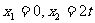
 ,即:
,即: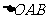 的面积为定值.
的面积为定值.
(2)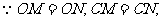
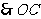 垂直平分线段
垂直平分线段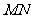 .
.
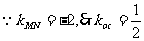 ,
,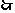 直线
直线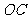 的方程是
的方程是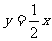 …………8分.
…………8分.
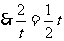 ,解得:
,解得: …………………………10分
…………………………10分
当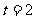 时,圆心
时,圆心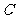 的坐标为
的坐标为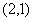 ,
,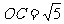 ,
,
此时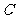 到直线
到直线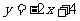 的距离
的距离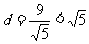 ,
,
圆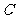 与直线
与直线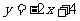 相交于两点.……………………12分
相交于两点.……………………12分
当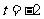 时,圆心
时,圆心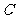 的坐标为
的坐标为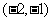 ,
,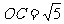 ,
,
此时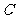 到直线
到直线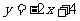 的距离
的距离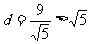
圆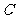 与直线
与直线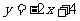 不相交,
不相交,
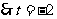 不符合题意舍去.……………………………………14分
不符合题意舍去.……………………………………14分
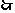 圆
圆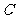 的方程为
的方程为 ……………………16分.
……………………16分.
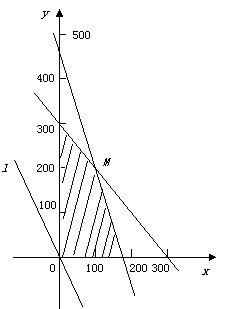
2、(湖北省荆门市2008届上期末)本地一公司计划2008年在省、市两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,省、市电视台的广告收费标准分别为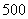 元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,规定省、市两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在省、市两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
解:设公司在省电视台和市电视台做广告的时间分别为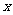 分钟
分钟
 和
和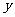 分钟,总收益为
分钟,总收益为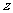 元,由题意得
元,由题意得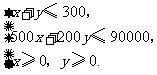
目标函数为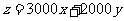 .
.
二元一次不等式组等价于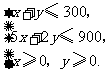
作出二元一次不等式组所表示的平面区域,即可行域.
如图:
作直线 ,
,
即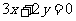 .
.
平移直线 ,从图中可知,当直线
,从图中可知,当直线 过
过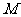 点时,目标函数取得最大值.
点时,目标函数取得最大值.
联立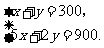 解得
解得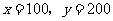 .
.
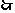 点
点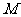 的坐标为
的坐标为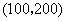 .
.
 (元)
(元)
答:该公司在省电视台做100分钟广告,在市电视台做200分钟广告,公司的收益最大,最大收益是70万元.
1、(广东省揭阳市2008年第一次模拟考试)为迎接2008年奥运会召开,某工艺品加工厂准备生产具有收藏价值的奥运会标志--“中国印·舞动的北京”和奥运会吉祥物--“福娃”.该厂所用的主要原料为A、B两种贵重金属,已知生产一套奥运会标志需用原料A和原料B的量分别为4盒和3盒,生产一套奥运会吉祥物需用原料A和原料B的量分别为5盒和10盒.若奥运会标志每套可获利700元,奥运会吉祥物每套可获利1200元,该厂月初一次性购进原料A、B的量分别为200盒和300盒.问该厂生产奥运会标志和奥运会吉祥物各多少套才能使该厂月利润最大,最大利润为多少?
解:设该厂每月生产奥运会标志和奥运会吉祥物分别为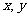 套,月利润为
套,月利润为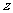 元,由题意得
元,由题意得
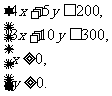 (
(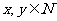 ) -----------------------4分
) -----------------------4分
目标函数为 …………5分
…………5分
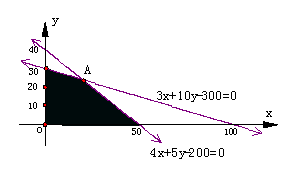
作出二元一次不等式组所表示的平面区域,即
可行域,如图: …………7分
目标函数可变形为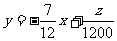 ,
,
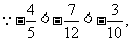
∴当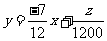 通过图中的点A时,
通过图中的点A时,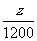 最大,这时Z最大。
最大,这时Z最大。
解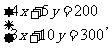 得点A的坐标为(20,24), …………10分
得点A的坐标为(20,24), …………10分
将点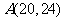 代入
代入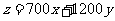 得
得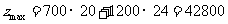 元
元
答:该厂生产奥运会标志和奥运会吉祥物分别为20,24套时月利润最大,最大利润为42800元
43、
42、(上海市部分重点中学2008届高三第二次联考)已知圆的半径为2,圆心在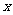 轴的正半轴上,且圆与直线3
轴的正半轴上,且圆与直线3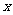 +
4
+
4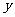 +4
= 0相切,则圆的标准方程是_______________________
+4
= 0相切,则圆的标准方程是_______________________
答案: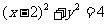
41、(山西大学附中2008届二月月考)直线l: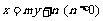 过点
过点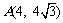 ,若可行域
,若可行域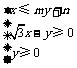 的外接圆的直径为
的外接圆的直径为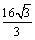 ,则实数n的值为________________.
,则实数n的值为________________.
答案:8
40、(江苏省南通通州市2008届高三年级第二次统一测试)已知两圆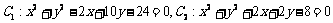 ,则以两圆公共弦为直径的圆的方程是
.
,则以两圆公共弦为直径的圆的方程是
.
答案: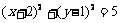
39、(江苏省南通通州市2008届高三年级第二次统一测试)在约束条件:x+2y≤5,2x+y≤4,x≥0,y≥0下,z=3x+4y的最大值是 .
答案:11
38、(江苏省南通通州市2008届高三年级第二次统一测试)若点(1,1)到直线xcosα+ysinα=2的距离为d,则d的最大值是 .
答案:2+
37、(江苏省泰兴市2007-2008学年第一学期高三调研)设直线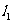 的方程为
的方程为 ,将直线
,将直线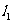 绕原点按逆时针方向旋转
绕原点按逆时针方向旋转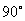 得到直线
得到直线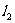 ,则
,则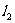 的方程是
的方程是
答案:2x-y+2=0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com