
53、(河南省濮阳市2008年高三摸底考试)直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
(1)求 ·
·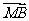 的取值范围;
的取值范围;
(2)过A、B两点分别作此抛物线的切线,两切线相交于N点.
求证: ·
· =0,
=0,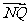 ∥
∥ .
.

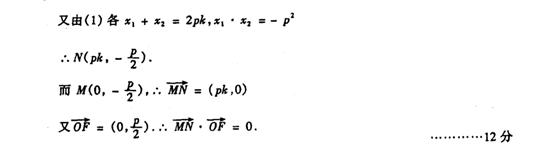
52、(河南省开封市2008届高三年级第一次质量检)双曲线 的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,
的左、右焦点分别为F1、F2,O为坐标原点,点A在双曲线的右支上,点B在双曲线左准线上,

(1)求双曲线的离心率e;
(2)若此双曲线过C(2,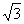 ),求双曲线的方程;
),求双曲线的方程;
(3)在(2)的条件下,D1、D2分别是双曲线的虚轴端点(D2在y轴正半轴上),过D1的直线l交双曲线M、N, 的方程。
的方程。
解:(1) 四边形F2ABO是平行四边形
四边形F2ABO是平行四边形


∴四边 形F2ABO是菱形.
∴
由双曲线定义得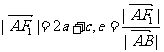
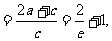
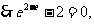

(2)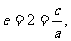
 ,双曲线方程为
,双曲线方程为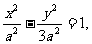
把点C 代入有
代入有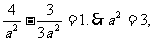
∴双曲线方程
(3)D1(0,-3),D2(0,3),设l的方程为
则由
因l与与双曲线有两个交点,


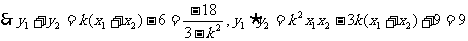

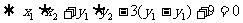
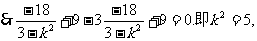
 故所求直线l方程为
故所求直线l方程为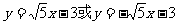
51、(河北省正定中学2008年高三第五次月考)已知直线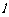 过椭圆E:
过椭圆E: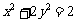 的右焦点
的右焦点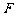 ,且与E相交于
,且与E相交于 两点.
两点.
 (1)设
(1)设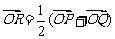 (
( 为原点),求点
为原点),求点 的轨迹方程;
的轨迹方程;
(2)若直线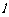 的倾斜角为60°,求
的倾斜角为60°,求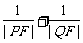 的值.
的值.
解:(1)设


由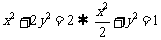 ,易得右焦点
,易得右焦点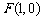 ----------(2分)
----------(2分)
当直线 轴时,直线
轴时,直线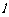 的方程是:
的方程是: ,根据对称性可知
,根据对称性可知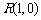
当直线 的斜率存在时,可设直线
的斜率存在时,可设直线 的方程为
的方程为
代入E有
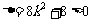 ;
; 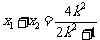 ----(5分)
----(5分)
于是
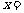
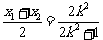 ;
; 
消去参数 得
得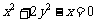 而
而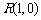 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是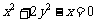 -(8分)
-(8分)
(2)设椭圆另一个焦点为 ,
,
在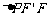 中
中 设
设 ,则
,则
由余弦定理得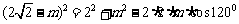

同理,在 ,设
,设 ,则
,则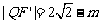
也由余弦定理得

于是 ---------(12分)
---------(12分)
50、(山东省郓城一中2007-2008学年第一学期期末考试)在直角坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P向y轴作垂线段PP′,P′为垂足.
(1)求线段PP′中点M的轨迹C的方程;
(2)过点Q(-2,0)作直线l与曲线C交于A、B两点,设N是过点 ,且以
,且以 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
解:(1)设M(x,y)是所求曲线上的任意一点,P(x1,y1)是方程x2 +y2 =4的圆上的任意一点,则
则有: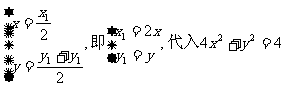 得,
得,
轨迹C的方程为
(1)当直线l的斜率不存在时,与椭圆无交点.
所以设直线l的方程为y = k(x+2),与椭圆交于A(x1,y1)、B(x2,y2)两点,N点所在直线方程为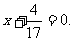
由
由△= 
即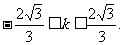 …
… 
 即
即 ,∴四边形OANB为平行四边形
,∴四边形OANB为平行四边形
假设存在矩形OANB,则 ,即
,即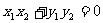 ,
,
即 ,
,
于是有 得
得 … 设
… 设 ,
,
即点N在直线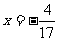 上.
上.
∴存在直线l使四边形OANB为矩形,直线l的方程为
49、过双曲线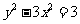 的上支上一点
的上支上一点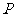 作双曲线的切线交两条渐近线分别于点
作双曲线的切线交两条渐近线分别于点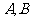 .
.
(1)求证: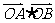 为定值;
为定值;
(2)若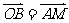 ,求动点
,求动点 的轨迹方程.
的轨迹方程.
解:(1)设直线AB: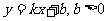
由 得
得
 …………………………………….3分
…………………………………….3分

…………………………………………………………………………………………….7分
(2)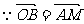 ,所以四边形BOAM是平行四边形
,所以四边形BOAM是平行四边形
 ……………………………………………………………….9分
……………………………………………………………….9分
 ①
①
 ②
②
由①②及 ……………………………………………..13分
……………………………………………..13分
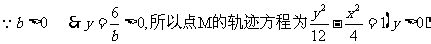 …………14分
…………14分
48、已知椭圆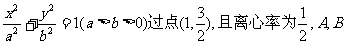 是椭圆上纵坐标不为零的两点,若
是椭圆上纵坐标不为零的两点,若 其中F为椭圆的左焦点.
其中F为椭圆的左焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)求线段AB的垂直平分线在y轴上的截距的取值范围.
解:(Ⅰ)由已知,得
 ………4分
………4分
(Ⅱ)∵A、B是椭圆上纵坐标不为零的点,
∴A、F、B三点共线,且直线AB的斜率存在且不为0.
又F(-1,0),则可记AB方程为 并整理得
并整理得
 ……………………………………6分
……………………………………6分
显然△>0,设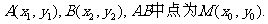
 ……………………8分
……………………8分
直线AB的垂直平分线方程为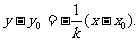
令x=0,得 ……………………………………10分
……………………………………10分
∵ “=”号,
“=”号,
∴ ,
,
所以所求的取值范围是 ……………………………………12分
……………………………………12分
47、(河北省正定中学高2008届一模)已知椭圆 的离心率为
的离心率为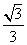 ,直线
,直线 :
: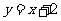 与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C1的短半轴长为半径的圆相切.
(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点F2,直线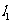 过点F1且垂直于椭圆的长轴,动直线
过点F1且垂直于椭圆的长轴,动直线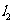 垂直
垂直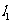 于点P,线段PF2垂直平分线交
于点P,线段PF2垂直平分线交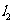 于点M,求点M的轨迹C2的方程;
于点M,求点M的轨迹C2的方程;
(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足 ,求
,求 的取值范围.
的取值范围.
解:(本小题满分12分)
解:(1) ,
,
∵直线l:x-y+2=0与圆x2+y2=b2相切,∴ =b,∴b=
=b,∴b= ,b2=2,∴a3=3. ∴椭圆C1的方程是
,b2=2,∴a3=3. ∴椭圆C1的方程是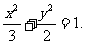 ……………………………….(3分)
……………………………….(3分)
(2)∵MP=MF,
∴动点M到定直线l1:x=-1的距离等于它的定点F2(1,0)的距离,
∴动点M的轨迹是以l1为准线,F2为焦点的抛物线,
∴点M的轨迹C2的方程为 。 ………………………………………….(7分)
。 ………………………………………….(7分)
(3)Q(0,0),设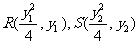 ,
,
 ,
,
由 得
得 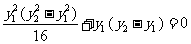 ,
,
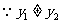 ,
,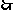 化简得
化简得 ,
,
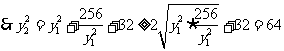
当且仅当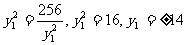 时等号成立,
时等号成立,
 ,又∵y22≥64,
,又∵y22≥64,
∴当 .
.
故 的取值范围是
的取值范围是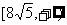 .…………………………………………….(12分)
.…………………………………………….(12分)
46、(河北衡水中学2008年第四次调考)已知平面上一定点C(4,0)和一定直线 为该平面上一动点,作
为该平面上一动点,作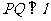 ,垂足为Q,且
,垂足为Q,且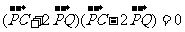 .
.
(1)问点P在什么曲线上?并求出该曲线的方程;
(2)设直线 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由.
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由.
解:(1)设P的坐标为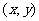 ,由
,由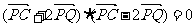 得
得
 (2分) ∴(
(2分) ∴(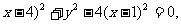 (4分)
(4分)
化简得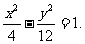 ∴P点在双曲线上,其方程为
∴P点在双曲线上,其方程为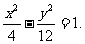 (6分)
(6分)
(2)设A、B点的坐标分别为 、
、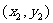 ,
,
由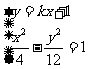 得
得 (7分)
(7分)
 ,(8分)
,(8分)
∵AB与双曲线交于两点,∴△>0,即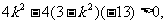
解得 (9分)
(9分)
∵若以AB为直径的圆过D(0,-2),则AD⊥BD,∴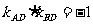 ,
,
即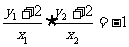 ,(10分)
,(10分)
∴
∴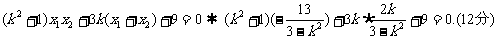
解得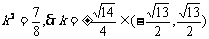 ,故满足题意的k值存在,且k值为
,故满足题意的k值存在,且k值为 .
.
45、(河北衡水中学2008年第四次调考)如图所示,已知圆 ,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足
,定点A(3,0),M为圆C上一动点,点P在AM上,点N在CM上,且满足 ,点N的轨迹为曲线E。
,点N的轨迹为曲线E。
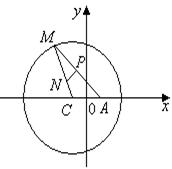 (1)求曲线E的方程;
(1)求曲线E的方程;
(2)求过点Q(2,1)的弦的中点的轨迹方程。
解:(1)∵
∴ 为
为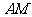 的中垂线,
的中垂线,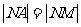 …………2分
…………2分
又因为 ,所以
,所以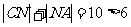
所以动点 的轨迹是以点
的轨迹是以点 和
和 为焦点的椭圆,
为焦点的椭圆,
且 …………4分
…………4分
所以曲线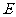 的方程为:
的方程为: ; …………6分
; …………6分
(2)设直线与椭圆交与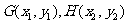 两点,中点为
两点,中点为
由点差法可得:弦的斜率 …………8分
…………8分
由 ,Q(2,1)两点可得弦的斜率为
,Q(2,1)两点可得弦的斜率为 ,…………10分
,…………10分
所以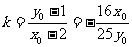 ,
,
化简可得中点的轨迹方程为: …………12分
…………12分
44、(河北衡水中学2008年第四次调考)已知曲线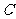 的方程为:
的方程为: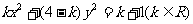
(1)若曲线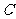 是椭圆,求
是椭圆,求 的取值范围;
的取值范围;
(2)若曲线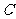 是双曲线,且有一条渐近线的倾斜角为
是双曲线,且有一条渐近线的倾斜角为 ,求此双曲线的方程.
,求此双曲线的方程.
解:(1)当

它表示椭圆的充要条件是
(2)方程表示双曲线的充要条件是:
当

其一条渐近线斜率为:
此时双曲线的方程为:
当 ,双曲线焦点在y轴上:
,双曲线焦点在y轴上:
其一条渐近线斜率为: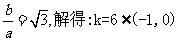
综上可得双曲线方程为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com