
63、(湖北省荆州市2008届高中毕业班质量检测)如图,已知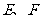 为平面上的两个定点,
为平面上的两个定点,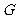 为动点,
为动点,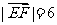 ,
,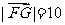 且
且 ,
,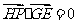 (
(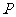 是
是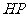 和
和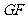 的交点)
的交点)
⑴建立适当的平面直角坐标系求出点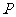 的轨迹方程;
的轨迹方程;
⑵若点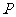 的轨迹上存在两个不同的点
的轨迹上存在两个不同的点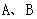 ,且线段
,且线段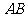 的中垂线与
的中垂线与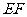 (或
(或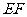 的延长线)相交于一点
的延长线)相交于一点 ,证明:
,证明: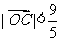 (
(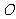 为
为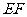 的中点)
的中点)
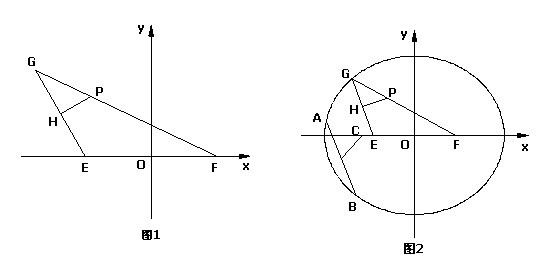
解:⑴如图1,以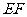 所在的直线为
所在的直线为 轴,
轴,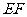 的中垂线为
的中垂线为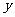 轴,建立平面直角坐标系
轴,建立平面直角坐标系
由题设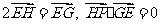
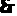
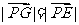 ,而
,而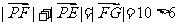
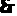 点
点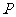 是以
是以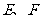 为焦点、长轴长为
为焦点、长轴长为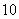 的椭圆,故点
的椭圆,故点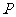 的轨迹方程为
的轨迹方程为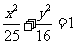 (6分)
(6分)
⑵如图2,设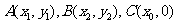 ,
,
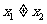 ,且
,且 ,
,
即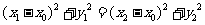 ,又
,又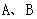 在轨迹上,
在轨迹上,
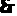
 即
即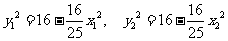
代入整理得:
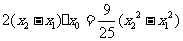
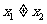 ,
,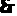
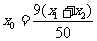 (10分)
(10分)
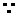
 ≤
≤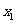 ≤
≤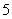 ,
, ≤
≤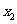 ≤
≤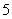 ,
,
 ≤
≤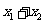 ≤
≤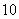
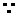
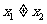 ,
,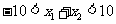
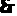
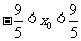 ,即
,即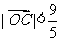 。
。
62、(湖北省荆门市2008届上期末)已知F1、F2为双曲线C: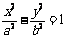 的左、右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左、右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: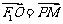 ,
,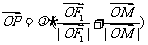 (λ>0)
(λ>0)
(1)求此双曲线的离心率;
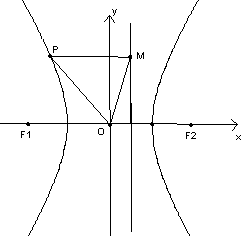 (2)若过点N(
(2)若过点N(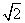 ,
, )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且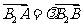 ,
,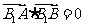 ,求双曲线C和直线AB的方程.
,求双曲线C和直线AB的方程.
解:(1)法一:依题意四边形OF1PM为菱形,设P(x,y)则F1(-c,0),M(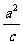 ,y)
,y)
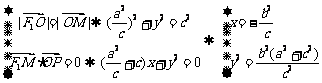 代入
代入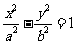 得
得
 化简得e=2
……………4分
化简得e=2
……………4分
法二: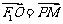
 OF1PM为平行四边形,
OF1PM为平行四边形,
又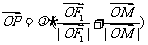 (λ>0)知P在
(λ>0)知P在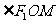 的角平分线上
的角平分线上
∴四边形OF1PM为菱形,且边长为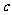 ,∴
,∴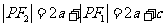 ………4分
………4分
由第二定义知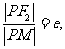 即
即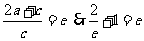 又
又
(2) ∴双曲线C的方程为
∴双曲线C的方程为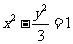 ……………8分
……………8分
∵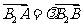 ∴过B2的直线交曲线C于A、B两点,且
∴过B2的直线交曲线C于A、B两点,且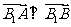
设直线AB: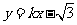 代入
代入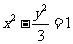 得
得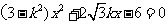

设A(x1,y1),B(x2,y2)由 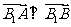
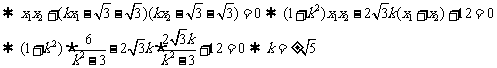
 ∴直线AB的方程为
∴直线AB的方程为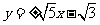
61、(湖北省黄冈市2007年秋季高三年级期末考试)在△ABC中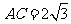 ,B是椭圆
,B是椭圆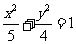 在x轴上方的顶点,
在x轴上方的顶点,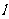 是双曲线
是双曲线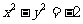 位于x轴下方的准线,当AC在直线
位于x轴下方的准线,当AC在直线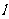 上运动时。
上运动时。
(1)求△ABC外接圆的圆心P的轨迹E的方程;
(2)过定点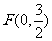 作互相垂直的直线
作互相垂直的直线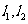 ,分别交轨迹E于M、N和R、Q,求四边形MRNQ面积的最小值。
,分别交轨迹E于M、N和R、Q,求四边形MRNQ面积的最小值。
解:(1)由椭圆方程 及双曲线方程
及双曲线方程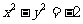 可得点
可得点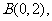 直线
直线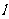 方程是
方程是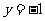
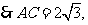 且
且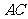 在直线
在直线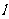 上运动。
上运动。
可设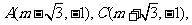
则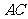 的垂直平分线方程为
的垂直平分线方程为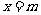 ①
①
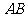 的垂直平分线方程为
的垂直平分线方程为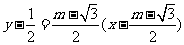 ②
②
 P是△ABC的外接圆圆心,
P是△ABC的外接圆圆心,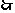 点P的坐标
点P的坐标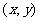 满足方程①和②
满足方程①和②
由①和②联立消去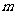 得
得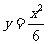
故圆心P的轨迹E的方程为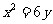
(2)由图可知,直线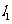 和
和 的斜率存在且不为零,设
的斜率存在且不为零,设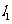 的方程为
的方程为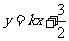 ,
,
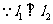 ,
,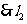 的方程为
的方程为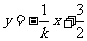
由
得 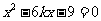
 △=
△=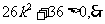 直线
直线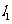 与轨迹E交于两点。
与轨迹E交于两点。
设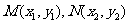 ,则
,则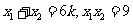 。
。
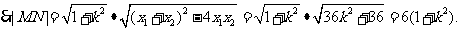
同理可得: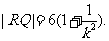
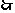 四边形MRNQ的面积
四边形MRNQ的面积

当且仅当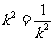 ,即
,即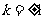 时,等号成立。
时,等号成立。
故四边形MNRQ的面积的最小值为72。(13分)
60、(湖北省黄冈市麻城博达学校2008届三月综合测试)已知直线 相交于A、B两点,M是线段AB上的一点,
相交于A、B两点,M是线段AB上的一点,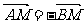 ,且点M在直线
,且点M在直线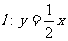 上.
上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若椭圆的焦点关于直线l的对称点在单位圆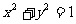 上,求椭圆的方程.
上,求椭圆的方程.
解:(Ⅰ)由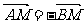 知M是AB的中点,
知M是AB的中点,
设A、B两点的坐标分别为
由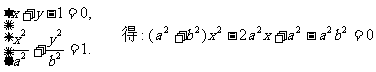
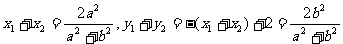 ,
,
∴M点的坐标为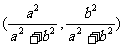 4分
4分
又M点的直线l上: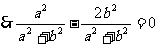

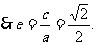 7分
7分
(Ⅱ)由(Ⅰ)知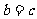 ,不妨设椭圆的一个焦点坐标为
,不妨设椭圆的一个焦点坐标为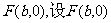 关于直线l:
关于直线l:
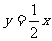 上的对称点为
上的对称点为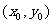 ,
,
则有 10分
10分
由已知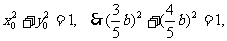
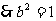 ,∴所求的椭圆的方程为
,∴所求的椭圆的方程为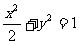 12分
12分
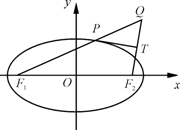
59、(湖北省鄂州市2008年高考模拟)已知椭圆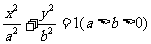 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足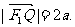 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足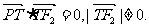
(Ⅰ)设 为点P的横坐标,证明
为点P的横坐标,证明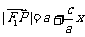 ;
;
(Ⅱ)求点T的轨迹C的方程;
 (Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=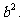 若存在,求∠F1MF2的正切值;若不存在,请说明理由.
若存在,求∠F1MF2的正切值;若不存在,请说明理由.
解 (Ⅰ)设点P的坐标为(x,y),由P(x,y)在椭圆上,得
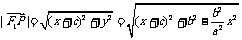
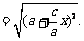
又由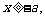 知
知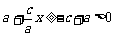 ,
,
所以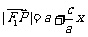
(Ⅱ) 当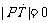 时,点(
时,点(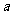 ,0)和点(-
,0)和点(-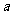 ,0)在轨迹上.
,0)在轨迹上.
当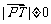 且
且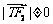 时,由
时,由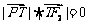 ,得
,得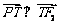 .
.
又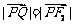 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,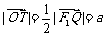 ,所以有
,所以有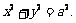
综上所述,点T的轨迹C的方程是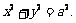
(Ⅲ) C上存在点M(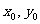 )使S=
)使S=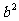 的充要条件是
的充要条件是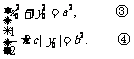
由③得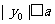 ,由④得
,由④得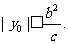 所以,当
所以,当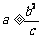 时,存在点M,使S=
时,存在点M,使S=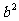 ;
;
当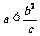 时,不存在满足条件的点M.
时,不存在满足条件的点M.
当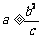 时,
时,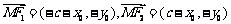 ,
,
由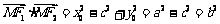 ,
,
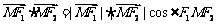 ,
,
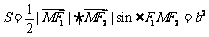 ,得
,得
 [总结点评]平面向量与椭圆的综合问题是《考试大纲》所
[总结点评]平面向量与椭圆的综合问题是《考试大纲》所
强调的问题,应熟练掌握其解题技巧,一般地,在这类问题
种,平面向量只起“背景”或“结论”的作用,几乎都不会
在向量的知识上设置障碍,所考查的核心内容仍然是解析几
何的基本方法和基本思想,比如本题(Ⅰ)本质是焦半径公
式,核心内容还是椭圆的第二定义的转化思想.(Ⅱ) 由
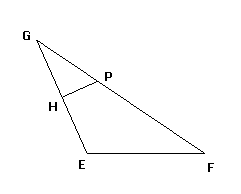
“PT其实为线段QF2的垂直平分线”可联想到下面的题目:如右图,Q为长轴为2a椭圆上一动点,QP是∠F1QF2的外角平分线,且F1P⊥QP,延长F2Q,使F2Q与F1P交于点M,则|QF1|=|QM|,所以点M的轨迹是以F2为圆心2a为半径的圆,进一步可得到P的轨迹是以O为圆心a为半径的圆.
58、(湖北省三校联合体高2008届2月测试)已知半圆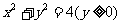 ,动圆
,动圆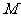 与此半圆相切且与
与此半圆相切且与 轴相切。
轴相切。
(1)求动圆圆心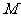 的轨迹方程。
的轨迹方程。
(2)是否存在斜率为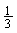 的直线
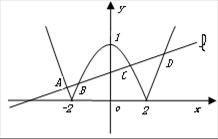
的直线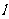 ,它与(1)中所得轨迹由左到右顺次交于A、B、C、D四个不同的点,且满足|AD|=2|BC|?若存在,求出
,它与(1)中所得轨迹由左到右顺次交于A、B、C、D四个不同的点,且满足|AD|=2|BC|?若存在,求出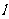 的方程,若不存在,说明理由。
的方程,若不存在,说明理由。
(1)设动圆圆心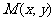 ,作
,作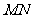 ⊥
⊥ 轴于点
轴于点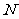
①若两圆外切: 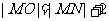 ,则
,则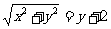 化简得:
化简得:
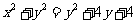

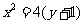
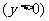 ……………3分
……………3分
 ②若两圆内切:
②若两圆内切: 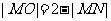 ,则
,则

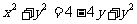

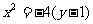
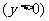 ……………5分
……………5分
综上,动圆圆心的轨迹方程是
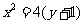
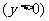 及
及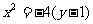
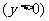 ………6分
………6分
其图象为两条抛物线位于 轴上方的部分,如图所示。
轴上方的部分,如图所示。
(2)假设直线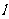 存在,可设
存在,可设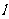 的方程为
的方程为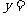
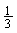
 。
。

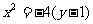
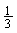

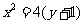 依题意得,它与曲线
依题意得,它与曲线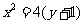 交于点
交于点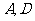 ,与曲线
,与曲线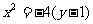 交于点
交于点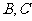 。
。
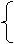
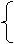 即
即
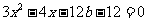 ①
①
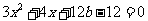 ②
②
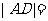
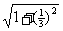
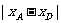 ,
, 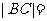
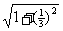
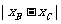

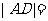 2
2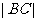
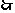
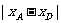 =2
=2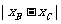
即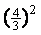 +
+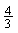
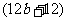 =4
=4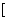
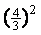 -
-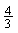
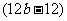 得
得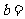
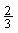 ……………11分
……………11分
将其代入方程①得 
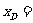

因为曲线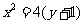 的横坐标范围为
的横坐标范围为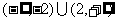 ,所以这样的直线
,所以这样的直线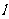 不存在。……………13分
不存在。……………13分
57、(湖北省八校高2008第二次联考)已知A,B是抛物线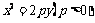 上的两个动点,
上的两个动点,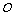 为坐标原点,非零向量
为坐标原点,非零向量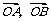 满足
满足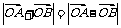 .
.
(Ⅰ)求证:直线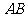 经过一定点;
经过一定点;
(Ⅱ)当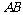 的中点到直线
的中点到直线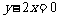 的距离的最小值为
的距离的最小值为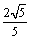 时,求
时,求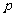 的值.
的值.
解: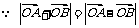 ,
, 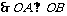 .设A,B两点的坐标为(
.设A,B两点的坐标为(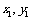 ),(
),( )则
)则
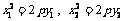 .
.
(1)经过A,B两点的直线方程为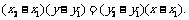
由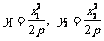 ,得
,得
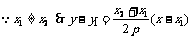 .
令
.
令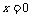 ,得
,得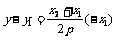 ,
, 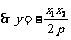 .
.
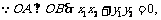 从而
从而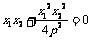 .
. 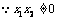 (否则,
(否则, 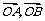 有一个为零向量),
有一个为零向量),
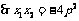 . 代入①,得
. 代入①,得 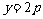 ,
,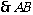 始终经过定点
始终经过定点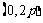 . ……………(6分)
. ……………(6分)
(2)设AB中点的坐标为(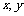 ),则
),则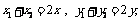
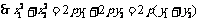 .
.
又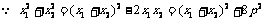 ,
, 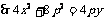 ,
,
即 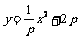 .……………①
.……………①
AB的中点到直线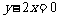 的距离
的距离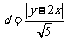 .
.
将①代入,得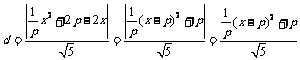 .
.
因为d的最小值为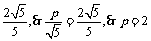 . ……………(12分)
. ……………(12分)
(若用导数求切线的斜率为2的切点坐标,参考给分.)
56、(黑龙江省哈尔滨九中2008年第三次模拟考试)已知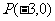 ,点
,点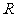 在
在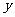 轴上,点
轴上,点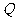 在
在 的正半轴上,点
的正半轴上,点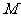 在直线
在直线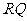 上,且
上,且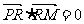
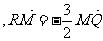 .
.
(1)当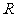 在
在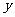 轴上移动时,求
轴上移动时,求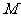 点轨迹C;
点轨迹C;
(2)若曲线 的准线交
的准线交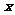 轴于
轴于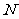 ,过
,过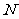 的直线交曲线
的直线交曲线 于两点
于两点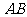 ,又
,又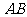 的中垂线交
的中垂线交 轴于点
轴于点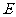 ,求
,求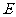 横坐标取值范围;
横坐标取值范围;
(3)在(2)中,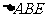 能否为正三角形.
能否为正三角形.
解:(1)设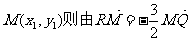 得
得
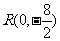 又由
又由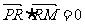 得
得 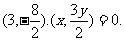
即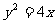 …………………………4分
…………………………4分
(2)由(1)知N(-1,0)设得:
由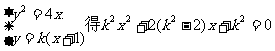
由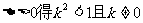
设
对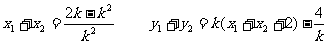
∴AB的中点为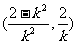
∴AB的中点为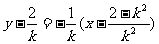
令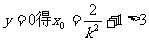
即x0>3.
55、(河南省许昌市2008年上期末质量评估)已知椭圆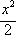 +y2=l的左焦点为F,O为坐标原点.
+y2=l的左焦点为F,O为坐标原点.
( I )求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(Ⅱ)设过点F的直线交椭圆于A、B两点,并且线段AB的中点在直线x+y=0上,求直线AB的方程.

54、设圆满足:(1)截直线y=x所得弦长为2;(2)被直线y=-x分成的一段劣弧所在的扇形面积是圆面积的倍.在满足条件(1)、(2)的所有圆中,求圆心到直线x+3y=0的距离最小的圆的的方程.
解:设所求圆的圆心为P(a,b),半径为r,
则P到直线y=x、直线y=-x的距离分别为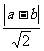 、
、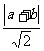 .………(2分)
.………(2分)
由题设知圆P截直线y=-x所得劣弧所对圆心角为90°,
圆P截直线y=-x所得弦长为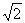 r,故r2=
r,故r2=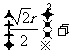 (
(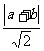 )2,
)2,
即r2=(a+b)2,……………………(4分)
又圆P截直线y=x所得弦长为2,所以有r2=1+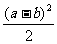 ,
,
从而有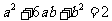 .……………………(6分)
.……………………(6分)
又点P到直线x+3y=0的距离为d=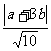 ,
,
所以10d2=|a+3b|2=a2+6ab+9b2=8b2+2≥2……………………(8分)
当且仅当b=0时上式等号成立,
此时5d2=1,从而d取得最小值,由此有a=±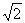 ,r=
,r=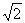 .…………(10分)
.…………(10分)
于是所求圆的方程为(x-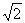 )2+y2=2或(x-
)2+y2=2或(x-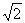 )2+y2=2…………(12分)
)2+y2=2…………(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com