
83、(山东省实验中学2008届高三第三次诊断性测试)已知椭圆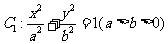 的离心率为,直线
的离心率为,直线 :
: 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆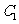 的方程;
的方程;
(2)设椭圆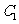 的左焦点为
的左焦点为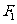 ,右焦点
,右焦点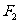 ,直线
,直线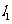 过点
过点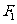 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直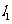 于点
于点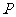 ,线段
,线段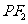 垂直平分线交
垂直平分线交 于点
于点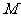 ,求点
,求点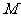 的轨迹
的轨迹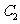 的方程;
的方程;
(3)设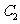 与
与 轴交于点
轴交于点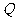 ,不同的两点
,不同的两点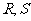 在
在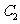 上,且满足
上,且满足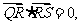 求
求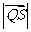 的取值范围.
的取值范围.
解:(Ⅰ)∵ ……1分
……1分
∵直线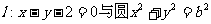 相切,
相切,
∴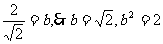 …………2分
…………2分
∴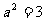 …………3分
…………3分
∵椭圆C1的方程是 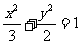 ………………4分
………………4分
(Ⅱ)∵MP=MF2,
∴动点M到定直线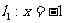 的距离等于它到定点F1(1,0)的距离,
的距离等于它到定点F1(1,0)的距离,
∴动点M的轨迹是C为l1准线,F2为焦点的抛物线 ………………6分
∴点M的轨迹C2的方程为 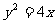 …………7分
…………7分
(Ⅲ)Q(0,0),设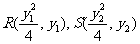 …………8分
…………8分
∴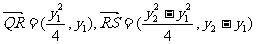 …………9分
…………9分
∵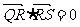
∴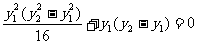
∵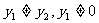 ,化简得
,化简得
∴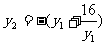 ………………11分
………………11分
∴
当且仅当 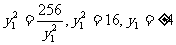 时等号成立 …………13分
时等号成立 …………13分
∵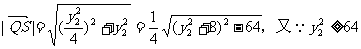
∴当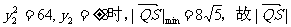 的取值范围是
的取值范围是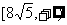 ……14分
……14分
82、(山东省聊城市2008届第一期末统考)已知定点A(-2,0),动点B是圆F: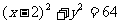 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹E的方程;
(2)直线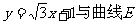 交于M,N两点,试问在曲线E位于第二象限部分上是否存在一点C,使
交于M,N两点,试问在曲线E位于第二象限部分上是否存在一点C,使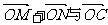 共线(O为坐标原点)?若存在,求出点C的坐标;若不存在,请说明理由.
共线(O为坐标原点)?若存在,求出点C的坐标;若不存在,请说明理由.
解:(1)由题意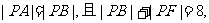
∴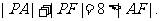
因此点P的轨迹是以A,F为焦点的椭圆.……………………4分
设所求椭圆的方程为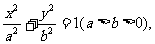
∴
∴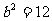
∴点P的轨迹方程为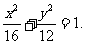 …………………………6分
…………………………6分
(2)假设存在满足题意的点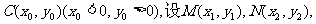
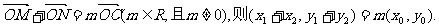
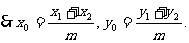
由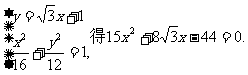 ……………………8分
……………………8分
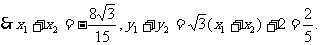
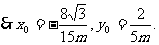 ……………………10分
……………………10分
又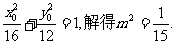
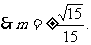
又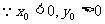
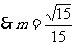
所以存在满足题意的点C(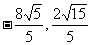 )……………………12分
)……………………12分
81、(宁夏区银川一中2008届第六次月考)如图,直线y=kx+b与椭圆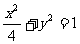 交于A、B两点,记△AOB的面积为S.
交于A、B两点,记△AOB的面积为S.
(I)求在k=0,0<b<1的条件下,S的最大值;
 (II)当|AB|=2,S=1时,求直线AB的方程.
(II)当|AB|=2,S=1时,求直线AB的方程.
解:(Ⅰ)解:设点 的坐标为
的坐标为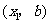 ,点
,点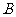 的坐标为
的坐标为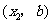 ,
,
由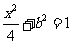 ,解得
,解得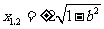 ,
,
所以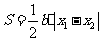
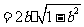
 .
.
当且仅当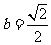 时,
时,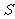 取到最大值
取到最大值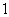 .
.
(Ⅱ)解:由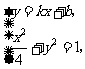
得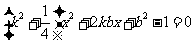 ,
,
 ,
,

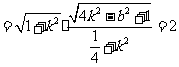 .
②
.
②
设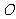 到
到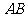 的距离为
的距离为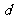 ,则
,则
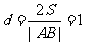 , 又因为
, 又因为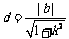 ,
,
所以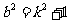 ,代入②式并整理,得
,代入②式并整理,得
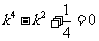 ,
,
解得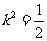 ,
,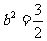 ,代入①式检验,
,代入①式检验, ,
,
故直线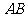 的方程是
的方程是
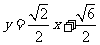 或
或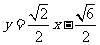 或
或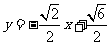 ,或
,或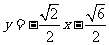 .
.
80、(江西省鹰潭市2008届高三第一次模拟)椭圆C: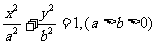 的两个焦点分别为
的两个焦点分别为
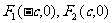 ,
,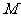 是椭圆上一点,且满足
是椭圆上一点,且满足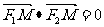 。
。
(1)求离心率e的取值范围
(2)当离心率e取得最小值时,点N( 0 , 3 )到椭圆上的点的最远距离为5
(i)求此时椭圆C的方程
(ii)设斜率为k(k¹0)的直线l与椭圆C相交于不同的两点A、B,Q为AB的中点,问A、B两点能否关于过点P(0,- )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由。
解:(1)、由几何性质知的取值范围为:≤e<1………………3分
(2)、(i) 当离心率e取最小值时,椭圆方程可表示为+ = 1 。设H( x , y )是椭圆上的一点,则| NH |2 =x2+(y-3)2 = - (y+3)2+2b2+18 ,其中 - b≤y≤b
若0<b<3 ,则当y = - b时,| NH |2有最大值b2+6b+9 ,所以由b2+6b+9=50解得b = -3±5(均舍去) …………………5分
若b≥3,则当y = -3时,| NH |2有最大值2b2+18 ,所以由2b2+18=50解得b2=16
∴所求椭圆方程为+ = 1………………7分
(ii) 设 A( x1 , y1 ) ,B( x2 , y2 ),Q( x0 , y0 ),则由两式相减得x0+2ky0=0;………① ……………………8分
又直线PQ⊥直线l,∴直线PQ的方程为y= - x - ,将点Q( x0 , y0 )坐标代入得y0= - x0- ………② ……………………9分
由①②解得Q( - k , ),而点Q必在椭圆的内部
∴ + < 1,…………… 10分
由此得k2 < ,又k≠0
∴ - < k < 0或0 < k <
故当( - , 0 ) ∪( 0 , )时,A、B两点关于过点P、Q、的直线对称。…………12分
79、(江苏省南通通州市2008届高三年级第二次统一测试)设A、B是抛物线y=2x2上两点,求证:AB的垂直平分线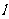 经过抛物线焦点的充要条件是线段AB的中点落在y 轴上。
经过抛物线焦点的充要条件是线段AB的中点落在y 轴上。
证明:设A(x1,y1),B(x2,y2),AB的中点落在y 轴上即x1+x2=0;
∵抛物线y=2x2的焦点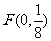 3′
3′
充分性:当AB的中点落在y 轴上即x1+x2=0时,y1=y2,A、B关于y轴对称,直线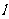 即为y轴,经过抛物线的焦点。
6′
即为y轴,经过抛物线的焦点。
6′
必要性:
(1)直线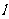 的斜率不存在且经过
的斜率不存在且经过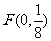 时,直线
时,直线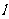 即为y轴,A、B关于y轴对称,AB的中点落在y 轴上。
即为y轴,A、B关于y轴对称,AB的中点落在y 轴上。
(2)直线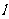 经过
经过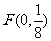 且斜率存在,设斜率为k(显然k≠0),截距为
且斜率存在,设斜率为k(显然k≠0),截距为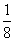 ,
,
即直线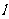 :y=kx+
:y=kx+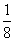
由已知得:
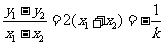 ≠0
≠0
即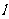 的斜率存在时,AB的中点不可能落在y 轴上即题设A、B点不存在。 9′
的斜率存在时,AB的中点不可能落在y 轴上即题设A、B点不存在。 9′
综上所述,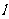 经过抛物线焦点的充要条件是线段AB的中点落在y 轴上。 10′
经过抛物线焦点的充要条件是线段AB的中点落在y 轴上。 10′
78、(江苏省南通通州市2008届高三年级第二次统一测试)倾斜角为60°的一束平行光线,将一个半径为 的球投影在水平地面上,形成一个椭圆.若以该椭圆的中心为原点,较长的对称轴为x轴,建立平面直角坐标系.
的球投影在水平地面上,形成一个椭圆.若以该椭圆的中心为原点,较长的对称轴为x轴,建立平面直角坐标系.
(1)求椭圆的标准方程;
(2)若球的某一条直径的两个端点在地面上的投影恰好分别落在椭圆边界的A、B两点上,且已知C(-4,0),求·的取值范围.
解:(1)设椭圆方程是,由题知b= ,2a=
,2a=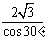 ,a=2
,a=2
所求椭圆的标准方程是. 6′
(2)设A(x1,y1),B(x2,y2),A、B关于坐标原点O对称,
=(x1+4,y1),=(x2+4,y2),
·=(x1+4,y1)·(x2+4,y2)=x1x2+4(x1+x2)+16+y1y2
= x1x2+16+y1y2 9′
AB与x轴不垂直时,设直线AB的方程是y=kx,代入椭圆方程得:
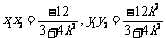
·=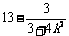 12′
12′
由于k可以取任意实数,故·∈[12,13), 14′
AB与x轴垂直时,||=||=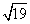 ,cos∠ACB=
,cos∠ACB=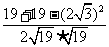 =
=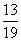
·=13
∴·∈[12,13]. 16′
77、(江苏省前黄高级中学2008届高三调研)在平面直角坐标系 中,直线
中,直线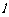 与抛物线
与抛物线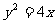 相交于不同的
相交于不同的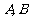 两点.
两点.
(Ⅰ)如果直线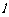 过抛物线的焦点,求
过抛物线的焦点,求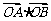 的值;
的值;
(Ⅱ)如果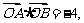 证明直线
证明直线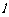 必过一定点,并求出该定点.
必过一定点,并求出该定点.
解:(Ⅰ)由题意:抛物线焦点为(1,0)
设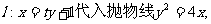 消去x得
消去x得
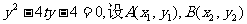
则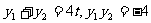 ,
,
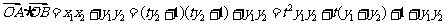
=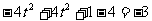
(Ⅱ)设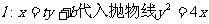 消去x,得
消去x,得
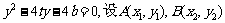 ,则y1+y2=4t ,y1y2=-4b。
,则y1+y2=4t ,y1y2=-4b。
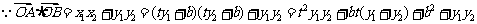
=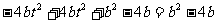 。
。
令 ,∴直线l过定点(2,0)。
,∴直线l过定点(2,0)。
76、(江苏省前黄高级中学2008届高三调研)已知直线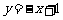 与椭圆
与椭圆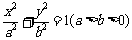 相交于A、B两点,且线段AB的中点在直线
相交于A、B两点,且线段AB的中点在直线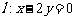 上.
上.
(Ⅰ)求此椭圆的离心率;
(Ⅱ)若椭圆的右焦点关于直线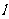 的对称点的在圆
的对称点的在圆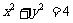 上,求此椭圆的方程.
上,求此椭圆的方程.
解:(1)设A、B两点的坐标分别为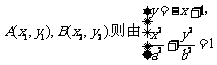 得
得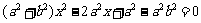 , 根据韦达定理,得
, 根据韦达定理,得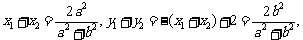
∴线段AB的中点坐标为(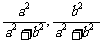 ).
).
由已知得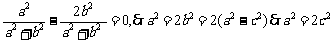
故椭圆的离心率为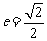
(2)由(1)知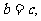 从而椭圆的右焦点坐标为
从而椭圆的右焦点坐标为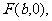 设
设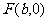 关于直线
关于直线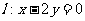 的对称点为
的对称点为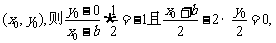 解得
解得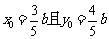 。由已知得
。由已知得 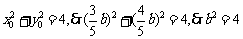 ,故所求的椭圆方程为
,故所求的椭圆方程为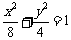 .
.
75、(江苏省南通市2008届高三第二次调研考试)已知椭圆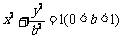 的左焦点为F,左、右顶点分别为A、C,上顶点为B.过F、B、C作⊙P,其中圆心P的坐标为(m,n).
的左焦点为F,左、右顶点分别为A、C,上顶点为B.过F、B、C作⊙P,其中圆心P的坐标为(m,n).
(Ⅰ)当m+n>0时,求椭圆离心率的范围;
(Ⅱ)直线AB与⊙P能否相切?证明你的结论.
解:(Ⅰ)设F、B、C的坐标分别为(-c,0),(0,b),(1,0),则FC、BC的中垂线分别为
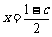 ,
,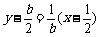 .………………………………………………………………2分
.………………………………………………………………2分
联立方程组,解出 ……………………………………………………………4分
……………………………………………………………4分
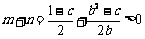 ,即
,即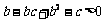 ,即(1+b)(b-c)>0,
,即(1+b)(b-c)>0,
∴ b>c. ……………………………………………………………………………………6分
从而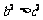 即有
即有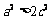 ,∴
,∴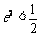 .……………………………………………………7分
.……………………………………………………7分
又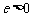 ,∴
,∴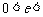
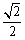 .
…………………………………………………………………8分
.
…………………………………………………………………8分
(Ⅱ)直线AB与⊙P不能相切.…………………………………………………………………9分
由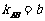 ,
,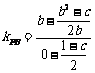 =
=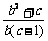 .
………………………………………………10分
.
………………………………………………10分
如果直线AB与⊙P相切,则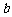 ·
·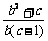 =-1. ………………………………………12分
=-1. ………………………………………12分
解出c=0或2,与0<c<1矛盾,………………………………………………………14分
所以直线AB与⊙P不能相切. …………………………………………………………15分
评讲建议:
此题主要考查直线与直线、直线与圆以及椭圆的相关知识,要求学生理解三角形外接圆圆心是三边中垂线的交点,从而大胆求出交点坐标,构造关于椭圆中a,b,c的齐次等式得离心率的范围.第二小题亦可以用平几的知识:圆的切割线定理,假设直线AB与⊙P相切,则有AB2=AF×AC,易由椭圆中a,b,c的关系推出矛盾.
74、(江苏省常州市北郊中学2008届高三第一次模拟检测)在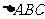 中,已知
中,已知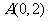 ,
,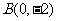 ,
,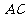 、
、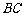 两边所在的直线分别与
两边所在的直线分别与 轴交于原点同侧的点
轴交于原点同侧的点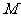 、
、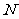 ,且满足
,且满足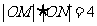 。
。
(1)求点 的轨迹方程
的轨迹方程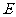 ;
;
(2)若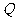 是
是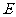 上任一点,动点
上任一点,动点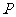 在线段
在线段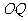 上,求
上,求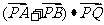 的最小值。
的最小值。
解:(1)设点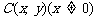 ,
,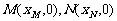 .
.
当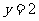 时,
时,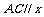 轴,当
轴,当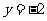 时,
时,
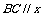 轴,与题意不符,所以
轴,与题意不符,所以 ;
;
由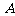 .
.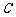 .
.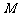 三点共线有
三点共线有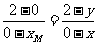 ,解得
,解得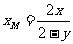 .同理由
.同理由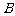 .
.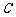 .
.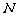 三点共线,解得
三点共线,解得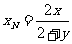 .
.
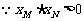 ,
, 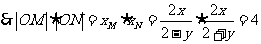 ,
,
化简得点 的轨迹方程为
的轨迹方程为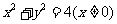
(2)解略。最小值为-2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com