
33、(福建省漳州一中2008年上期期末考试)如图所示,四棱锥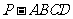 的底面为直角梯形,
的底面为直角梯形,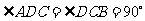 ,
,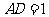 ,
, ,
,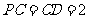 ,
, 底面
底面 ,
, 为
为 的中点.
的中点.
 (Ⅰ)求证:平面
(Ⅰ)求证:平面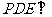 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成的角;
所成的角;
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
解法一:(Ⅰ)设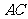 与
与 交点为
交点为 ,延长
,延长 交
交 的延长线于点
的延长线于点 ,
,
则 ,∴
,∴ ,∴
,∴ ,∴
,∴ ,
,
又∵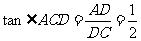 ,∴
,∴ ,
,
又∵ ,∴
,∴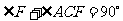 ,
,
∴ ,∴
,∴
又∵ 底面
底面 ,∴
,∴ ,∴
,∴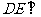 平面
平面 ,
,
∵ 平面
平面 ,∴平面
,∴平面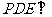 平面
平面 …………………………………(4分)
…………………………………(4分)
(Ⅱ)连结 ,过点
,过点 作
作 于
于 点,
点,
则由(Ⅰ)知平面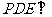 平面
平面 ,
,
且 是交线,根据面面垂直的性质,
是交线,根据面面垂直的性质,
 得
得 平面
平面 ,从而
,从而 即
即
 为直线
为直线 与平面
与平面 所成的角.
所成的角.
在 中,
中,
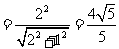 ,
,
在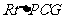 中,
中,

 . 所以有
. 所以有 ,
,
即直线 与平面
与平面 所成的角为
所成的角为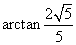 …………………………………(8分)
…………………………………(8分)
(Ⅲ)由于 ,所以可知点
,所以可知点 到平面
到平面 的距离等于点
的距离等于点 到平面
到平面 的距离的
的距离的 ,即
,即 . 在
. 在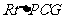 中,
中, ,
,
从而点 到平面
到平面 的距离等于
的距离等于 ………………………………………………(12分)
………………………………………………(12分)
解法二:如图所示,以点 为坐标原点,
为坐标原点,
 直线
直线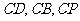 分别为
分别为 轴,
轴,
建立空间直角坐标系 ,
,
则相关点的坐标为
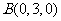 ,
, ,
,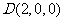 ,
, .
.
(Ⅰ)由于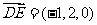 ,
, ,
,
 ,
,
所以 ,
,
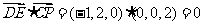 ,
,
所以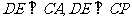 ,
,
而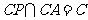 ,所以
,所以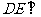 平面
平面 ,∵
,∵ 平面
平面 ,
,
∴平面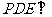 平面
平面 ……………………………………………………………(4分)
……………………………………………………………(4分)
(Ⅱ)设 是平面
是平面 的一个法向量,则
的一个法向量,则 ,
,
由于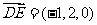 ,
,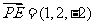 ,所以有
,所以有
 ,
,
令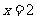 ,则
,则 ,即
,即 ,
,
再设直线 与平面
与平面 所成的角为
所成的角为 ,而
,而 ,
,
所以 ,
,
∴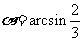 ,因此直线
,因此直线 与平面
与平面 所成的角为
所成的角为 ………………(8分)
………………(8分)
(Ⅲ)由(Ⅱ)知 是平面
是平面 的一个法向量,而
的一个法向量,而 ,
,
所以点 到平面
到平面 的距离为
的距离为
32、(福建省仙游一中2008届高三第二次高考模拟测试)在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB= ,EF=EC=1,
,EF=EC=1,
⑴求证:平面BEF⊥平面DEF;
⑵求二面角A-BF-E的大小。
解法1:⑴ ①证明: ∵平面ACEF⊥平面ABCD,EC⊥AC,
∴EC⊥平面ABCD;连接BD交AC于点O,连接FO,
∵正方形ABCD的边长为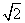 ,∴AC=BD=2;
,∴AC=BD=2;
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1;易求得DF=BF=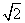 ,
,
DE=BE=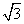 ,由勾股定理知 DF⊥EF,BF⊥EF,
,由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角,
 由BF=DF=
由BF=DF=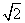 ,BD=2可知∠BFD=
,BD=2可知∠BFD= ,
,
∴平面BEF⊥平面DEF ………………(6分)
⑵取BF中点M,BE中点N,连接AM、MN、AN,
∵AB=BF=AF=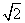 ,∴AM⊥BF,
,∴AM⊥BF,
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角。
易求得 ,
,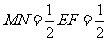 ;
;
在Rt△ 中,可求得
中,可求得 ,
,
∴在△ 中,由余弦定理求得
中,由余弦定理求得 ,
,
∴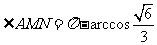 ……………………………(12分)
……………………………(12分)
解法2:⑴∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD;
建立如图所示的空间直角坐标系C-xyz,则

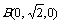 ,
, ,
, ,
, ,
,
∴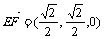 ,
,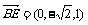 ,
, …(2分)
…(2分)
设平面BEF、平面DEF的法向量分别为
 ,则
,则
 ①
①
 ②,
②, ③,
③,  ④.
④.
由①③③④解得 ,∴
,∴ ,…(4分)
,…(4分)
∴ ,∴
,∴ ,故平面BEF⊥平面DEF…………(6分)
,故平面BEF⊥平面DEF…………(6分)
⑵设平面ABF的法向量为 ,∵
,∵ ,
,
∴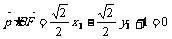 ,
, ,解得
,解得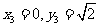
∴ ,………(8分)∴
,………(8分)∴ ……(10分)
……(10分)
由图知,二面角A-BF-E的平面角是钝角,故所求二面角的大小为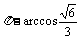
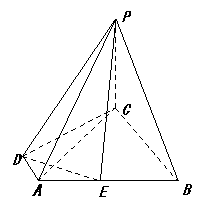
31、(福建省厦门市2008学年高三质量检查)
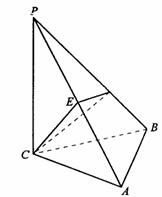 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB。
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB。
(1)求证:AB⊥平面PCB;
(2)求二面角C-PA-B的大小的余弦值。
(1)解:∵PC⊥平面ABC,AB 平面ABC,
平面ABC,
∴PC⊥AB。
∵CD⊥平面PAB,AB 平面PAB,
平面PAB,
∴CD⊥AB。
又PC∩CD=C,
∴AB⊥平面PCB。
(2)解法一:
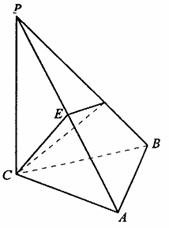 取AB的中点E,连结CE、DE。
取AB的中点E,连结CE、DE。
∵PC=AC=2,∴CE⊥PA,CE=
∵CD⊥平面PAB,
由三垂线定理的逆定理,得DE⊥PA。
∴∠CED为二面角C-PA-B的平面角。
由(1)AB⊥平面PCB,∴AB⊥BC,
又∵AB=BC,AC=2,求得BC=
(2)解法二:
∵AB⊥BC,AB⊥平面PBC,过点B作直线l∥PA,
 则l⊥AB,l⊥BC,以BC、BA、l所在直线为x、y、
则l⊥AB,l⊥BC,以BC、BA、l所在直线为x、y、
z轴建立空间直角坐标系(如图)。…………6分
设平面PAB的法向量为
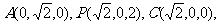

得 …………8分
…………8分
设平面PAC的法向量为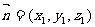 ,
,

解得 …………10分
…………10分
 …………11分
…………11分
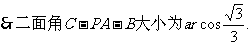 …………12分
…………12分
(2)解法三:
∵CD⊥平面PAB,∴ 是平面PAB的一个法向量。
是平面PAB的一个法向量。
取AC中点F,∵AB=BC= ,∴BF⊥AC,
,∴BF⊥AC,
又PC⊥平面ABC,有平面PAC⊥平面ABC,
∴BF⊥平面PAC,∴ 是平面PAC的一个法向量。
是平面PAC的一个法向量。
 …………7分
…………7分

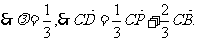 …………9分
…………9分
 …………10分
…………10分

45、
44、(上海市部分重点中学2008届高三第二次联考)设a,b,c表示三条直线, 表示两个平面,下列命题中不正确的是---------( )
表示两个平面,下列命题中不正确的是---------( )
A. 
 B.
B.  Þb⊥c
Þb⊥c
C.  D.
D. 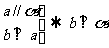
答案:D
43、(山西大学附中2008届二月月考)湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下一个直径为12cm,深2cm的空穴,则该球的表面积为_____________cm2.( )
)
答案:400π
42、(山东省郓城一中2007-2008学年第一学期期末考试)在1200的二面角 -l-β内有一点P,P在平面
-l-β内有一点P,P在平面 、β内的射影A、B分别落在半平面
、β内的射影A、B分别落在半平面 、β内,且PA=3,PB=4,则P到l的距离为
、β内,且PA=3,PB=4,则P到l的距离为
答案: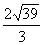
41、(山东省济南市2008年2月高三统考)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为2,2,3,则此球的表面积为 .
答案:17π
40、(江西省鹰潭市2008届高三第一次模拟)空间三条直线中,任何两条不共面,且两两互相垂直,直线 与这三条直线所成的角都为
与这三条直线所成的角都为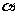 ,则
,则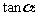 =
。
=
。
答案:
39、(江苏省南通通州市2008届高三年级第二次统一测试)已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题:
①若m∥β,n∥β,m、n α,则α∥β;
α,则α∥β;
②若α⊥γ,β⊥γ,α∩β=m,n γ,则m⊥n;
γ,则m⊥n;
③若m⊥α,α⊥β,m∥n,则n∥β;
④若n∥α,n∥β,α∩β=m,那么m∥n;
其中所有正确命题的序号是 .
答案:②④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com