
78、(江苏省南通通州市2008届高三年级第二次统一测试)如图已知在三棱柱ABC--A1B1C1中,AA1⊥面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
 (1)求证:面PCC1⊥面MNQ;
(1)求证:面PCC1⊥面MNQ;
(2)求证:PC1∥面MNQ.
主要得分步骤:(1)AB⊥面PCC1; 4′
MN∥AB,故MN⊥面MNQ
MN在平面MNQ内,∴面PCC1⊥面MNQ; 7′
(2)连AC1、BC1,BC1∥NQ,AB∥MN
面ABC1∥面MNQ 11′
PC1在面ABC1内.
∴PC1∥面MNQ. 13′
77、(江苏省泰兴市2007-2008学年第一学期高三调研)已知等腰梯形PDCB中(如图1),PB=3,DC=1,PB=BC= ,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
,A为PB边上一点,且PA=1,将△PAD沿AD折起,使面PAD⊥面ABCD(如图2).
(Ⅰ)证明:平面PAD⊥PCD;
(Ⅱ)试在棱PB上确定一点M,使截面AMC
把几何体分成的两部分 ;
;
(Ⅲ)在M满足(Ⅱ)的情况下,判断直线PD
是否平行面AMC.
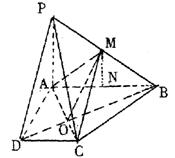
(I)证明:依题意知: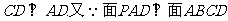
 …………2分
…………2分
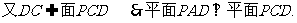 …4分
…4分
(II)由(I)知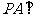 平面ABCD
平面ABCD
∴平面PAB⊥平面ABCD. …………5分
在PB上取一点M,作MN⊥AB,则MN⊥平面ABCD,
设MN=h
则
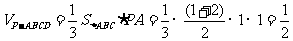 …………8分
…………8分
要使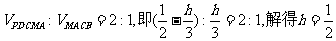
即M为PB的中点. …………10分
(Ⅲ)连接BD交AC于O,因为AB//CD,AB=2,CD=1,由相似三角形易得BO=2OD
∴O不是BD的中心……………………10分
又∵M为PB的中点
∴在△PBD中,OM与PD不平行
∴OM所以直线与PD所在直线相交
又OM 平面AMC
平面AMC
∴直线PD与平面AMC不平行.……………………15分
76、(江苏省前黄高级中学2008届高三调研)如图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.E、F分别是线段AB、BC上的点,且EB= FB=1.
(1)求直线EC1与FD1所成角的余弦值;
(2)求二面角C-DE-C1的平面角的正切值.
解:以A为原点, 分别为x轴,y轴,z轴的
分别为x轴,y轴,z轴的
正向建立空间直角坐标系A-xyz,则有D(0,3,0)、
D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2).
于是,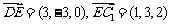 ,
,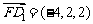 .
.
(1)设EC1与FD1所成角为b,则 .
.
(2)设向量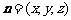 与平面C1DE垂直,则有
与平面C1DE垂直,则有
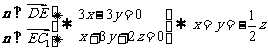 .
.
∴ 其中z>0.
其中z>0.
取n0=(-1,-1,2),则n0是一个与平面C1DE垂直的向量.
∵向量 =(0,0,2)与平面CDE垂直,
=(0,0,2)与平面CDE垂直,
∴n0与 所成的角θ为二面角C-DE-C1的平面角.
所成的角θ为二面角C-DE-C1的平面角.
∵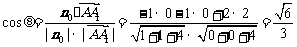 ,∴
,∴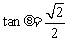 .
.
50、 (河北省正定中学2008年高三第五次月考)如图,在直三棱柱ABC-A1B1C1中,
(河北省正定中学2008年高三第五次月考)如图,在直三棱柱ABC-A1B1C1中,
 E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
(3)在(2)的条件下,求二面角A1-AG-E的大小(文科求其正切值)。
解:(1)取B1C1的中点E1,连A1E1,E1C,则AE∥A1E1,∴∠E1A1C是异面直线AE与A1C所成的角。设 ,则
,则
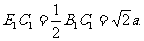

 中,
中,
 。
。
所以异面直线AE与A1C所成的角为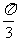 。 ------------------4分
。 ------------------4分
(2).由(1)知,A1E1⊥B1C1,又因为三棱柱ABC-A1B1C1是直三棱柱

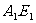 ⊥BCC1B1,又
⊥BCC1B1,又 EG⊥A1C
EG⊥A1C  CE1⊥EG.
CE1⊥EG.
 ∠
∠ =∠GEC
=∠GEC 
 ~
~
 即
即 得
得
所以G是CC1的中点 ---------------------------- --8分
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC.
又 平面ABC⊥平面ACC1A1
平面ABC⊥平面ACC1A1  EP⊥平面ACC1A1
EP⊥平面ACC1A1
而PQ⊥AG  EQ⊥AG.
EQ⊥AG. ∠PQE是二面角C-AG-E的平面角.
∠PQE是二面角C-AG-E的平面角.
由EP=a,AP=a,PQ=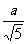 ,得
,得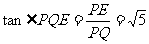
所以二面角C-AG-E的平面角是arctan,而所求二面角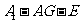 是二面角C-AG-E的补角,故二面角
是二面角C-AG-E的补角,故二面角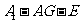 的平面角是π-arctan
------------------------12分
的平面角是π-arctan
------------------------12分
(文)二面角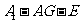 的平面角的正切值为-。------------------------12分
的平面角的正切值为-。------------------------12分
49、 矩形ABCD与矩形ABEF的公共边为AB,且平面ABCD
矩形ABCD与矩形ABEF的公共边为AB,且平面ABCD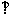 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD , AD=1, EF=
, AD=1, EF=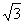 .
.
(Ⅰ)证明:AE 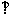 平面FCB;
平面FCB;
(Ⅱ)求异面直线BD与AE所成角的余弦值
(Ⅲ)若M是棱AB的中点,在线段FD上是
 否存在一点N,使得MN∥平面FCB?
否存在一点N,使得MN∥平面FCB?
证明你的结论.
解:(1)  平面ABCD
平面ABCD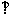 平面ABEF,
平面ABEF,
且四边形ABCD与ABEF是矩形,
 AD
AD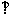 平面ABEF,
平面ABEF, AD
AD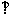 AE,
AE,
 BC∥AD
BC∥AD  BC
BC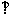 AE
AE
又FD=2,AD=1,所以AF=EF=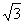 ,
,
所以四边形ABEF为正方形. AE
AE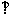 FB,
FB,
又BF BF
BF 平面BCF,BC
平面BCF,BC 平面BCF
平面BCF
所以AE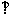 平面BCF……………………………………………4分
平面BCF……………………………………………4分
(2)设BF AE=O,取FD的中点为H,连接OH,在
AE=O,取FD的中点为H,连接OH,在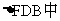 OH//BD,
OH//BD,

 HOF即为异面直线BD与AE所成的角(或补角),
HOF即为异面直线BD与AE所成的角(或补角),
在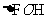 中,OH=1,FH=1,FO=
中,OH=1,FH=1,FO= ,
, cos
cos HOF=
HOF=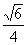
 异面直线BD与AE所成的角的余弦值为
异面直线BD与AE所成的角的余弦值为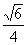 ………………………….8分
………………………….8分
(3)当N为FD的中点时, MN∥平面FCB
证明:取CD的中点G,连结NG,MG,MN,
则NG//FC,MG//BC,
又NG 平面NGM,MG
平面NGM,MG 平面NGM且NG
平面NGM且NG MG=G
MG=G
所以平面NGM//平面FBC,
 MN
MN 平面NGM
平面NGM
 MN//平面FBC……………………………………………………………12分
MN//平面FBC……………………………………………………………12分
48、(河北省正定中学高2008届一模)在五棱锥P-ABCDE中,PA=AB=AE=4a,PB=PE= a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若 为
为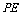 中点,求证:
中点,求证: 平面
平面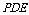 .
.
(2)求二面角A-PD-E的正弦值;(3)求点C到平面PDE的距离.
解(1)∵∠AED=90°,∴AE⊥ED.∵PA⊥平面ABCDE,∴PA⊥ED.∴ED⊥平面PAE,所以DE⊥AG。 ,
, 为
为 中点,所以AG⊥PE,DE∩PE=E,∴AG⊥平面PDE ………………………(4分)
中点,所以AG⊥PE,DE∩PE=E,∴AG⊥平面PDE ………………………(4分)
(2)∵∠AED=90°,∴AE⊥ED.
∵PA⊥平面ABCDE,∴PA⊥ED.∴ED⊥平面PAE.
过A作AG⊥PE于G,过DE⊥AG,∴AG⊥平面PDE.过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.∴∠AHG为二面角A-PD-E的平面角.
在直角△PAE中,AG=2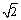 a.在直角△PAD中,AH=
a.在直角△PAD中,AH=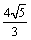 a
a
∴在直角△AHG中,sin∠AHG= =
= .
.
∴二面角A-PD-E的正弦值为 . …………………………………………..(
8分)
. …………………………………………..(
8分)
(3)∵∠EAB=∠ABC=∠DEA=90°, BC=DE=2a,AB=AE=4a,
取AE中点F,连CF,∵AF∥=BC,∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE,∴CF∥DE,而DE 平面PDE,CF
平面PDE,CF 平面PDE,
平面PDE,
∴CF∥平面PDE.∴点C到平面PDE的距离等于F到平面PDE的距离.
∵PA⊥平面ABCDE,∴PA⊥DE.
又∵DE⊥AE,∴DE⊥平面PAE.∴平面PAE⊥平面PDE.
∴过F作FG⊥PE于G,则FG⊥平面PDE.∴FG的长即F点到平面PDE的距离.在△PAE中,PA=AE=4a,F为AE中点,FG⊥PE,
∴FG=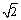 a.
∴点C到平面PDE的距离为
a.
∴点C到平面PDE的距离为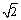 a.(或用等体积法求)…………(12分)
a.(或用等体积法求)…………(12分)
47、(安徽省合肥市2008年高三年级第一次质检)如图,在几何体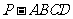 中,面
中,面 为矩形,
为矩形,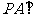 面
面 ,
,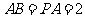
 (1)求证;当
(1)求证;当 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;
(2)当 时,求二面角
时,求二面角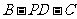 的取值范围。
的取值范围。
以A为坐标原点,射线AP、AB、AD分别为x轴、y轴、z轴的正半轴建立如图所示的坐标系。设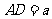 ,由已知得
,由已知得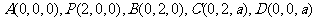
(1)当 时,
时, ,
,
 ∴
∴ 4分
4分
∴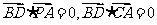 ,∴
,∴
又 ,∴平面PBD⊥平面PAC; 6分
,∴平面PBD⊥平面PAC; 6分
解法二:当 时,矩形
时,矩形 为正方形,∴
为正方形,∴
∵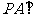 面
面 ,∴
,∴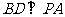 2分
2分
又 ,∴BD⊥平面PAC,BD
,∴BD⊥平面PAC,BD 平面PBD,∴平面PBD⊥平面PAC
平面PBD,∴平面PBD⊥平面PAC
(2)由
得
设 平面PDC,∴
平面PDC,∴
∴ 不妨设
不妨设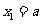 ,则
,则
设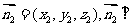 平面PDB,∴
平面PDB,∴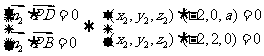
∴ 不妨设
不妨设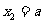 ,则
,则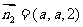 10分
10分
∴
当 变化时,即
变化时,即 ,
,

又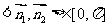 ,∴
,∴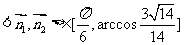
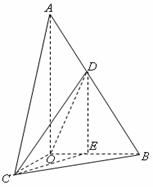
46、(贵州省贵阳六中、遵义四中2008年高三联考)如图,在 中,
中, ,斜边
,斜边 .
. 可以通过
可以通过 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角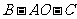 是直二面角.动点
是直二面角.动点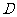 在斜边
在斜边 上。
上。
(I)求证:平面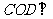 平面
平面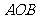 ;
;
(II)当 为
为 的中点时,求异面直线
的中点时,求异面直线 与
与 所
所
 成角的大小;
成角的大小;
(III)(理)求 与平面
与平面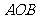 所成角的最大值。
所成角的最大值。
(文)当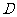 为
为 的中点时,求
的中点时,求 与平面
与平面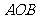 所成的角。
所成的角。
解:(I)由题意, ,
,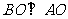 ,
, 是二面角
是二面角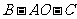 是直二面角,
是直二面角,
又 二面角
二面角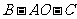 是直二面角,
是直二面角, ,又
,又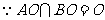 ,
,
 平面
平面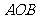 ,又
,又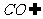 平面
平面 ,
, 平面
平面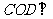 平面
平面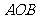 .……4分
.……4分
(II)解法一:作 ,垂足为
,垂足为 ,连结
,连结 (如图),则
(如图),则 ,
,
 是异面直线
是异面直线 与
与 所成的角.
所成的角.
在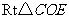 中,
中, ,
, ,
, .
.
又 .
. 在
在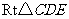 中,
中,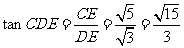 .
.
 异面直线
异面直线 与
与 所成角的大小为
所成角的大小为 .……8分
.……8分

解法二:建立空间直角坐标系 ,如图,则
,如图,则 ,
,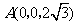 ,
, ,
,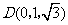 ,
, ,
, ,
,
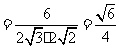 .
. 异面直线
异面直线 与
与 所成角的大小为
所成角的大小为 .……8分
.……8分
(III)(理)由(I)知,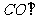 平面
平面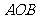 ,
,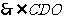 是
是 与平面
与平面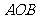 所成的角,
所成的角,
且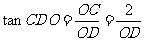 .当
.当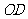 最小时,
最小时,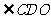 最大,这时,
最大,这时, ,垂足为
,垂足为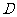 ,
, ,
,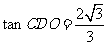 ,
, 与平面
与平面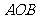 所成角的最大值为
所成角的最大值为 .……12分
.……12分
(文)由(I)知,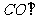 平面
平面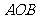 ,
,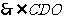 是
是 与平面
与平面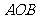 所成的角,且
所成的角,且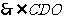 =45o。……12分
=45o。……12分
45、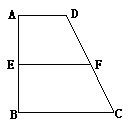 (广东省五校2008年高三上期末联考)已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =
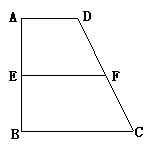
(广东省五校2008年高三上期末联考)已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =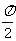 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
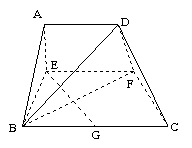 (3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
(3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
解:(1)(法一)∵平面 平面
平面 ,AE⊥EF,∴AE⊥面平面
,AE⊥EF,∴AE⊥面平面 ,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。…………………………………………… 1分
,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。…………………………………………… 1分
则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),E(0,0,0)…………2分

 (-2,2,2),
(-2,2,2),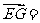 (2,2,0)…………………………………………………3分
(2,2,0)…………………………………………………3分

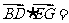 (-2,2,2)
(-2,2,2) (2,2,0)=0,∴
(2,2,0)=0,∴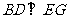 ……………………………4分
……………………………4分
(法二)作DH⊥EF于H,连BH,GH,……………1分
由平面 平面
平面 知:DH⊥平面EBCF,
知:DH⊥平面EBCF,
而EG 平面EBCF,故EG⊥DH。
平面EBCF,故EG⊥DH。
又四边形BGHE为正方形,∴EG⊥BH,
BH DH=H,故EG⊥平面DBH,………………… 3分
DH=H,故EG⊥平面DBH,………………… 3分
而BD 平面DBH,∴ EG⊥BD。………………… 4分
平面DBH,∴ EG⊥BD。………………… 4分
(或者直接利用三垂线定理得出结果)
(2)∵AD∥面BFC,
所以  VA-BFC=
VA-BFC= =
=
 4
4 (4-x)
(4-x) x
x
 ………………………………………………………………………7分
………………………………………………………………………7分
即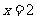 时
时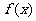 有最大值为
有最大值为 。…………………………………………………………8分
。…………………………………………………………8分
(3)(法一)设平面DBF的法向量为 ,∵AE=2, B(2,0,0),D(0,2,2),
,∵AE=2, B(2,0,0),D(0,2,2),
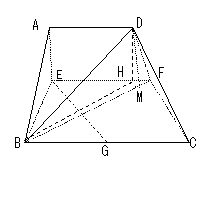 F(0,3,0),∴
F(0,3,0),∴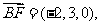
 (-2,2,2), ………………………………9分
(-2,2,2), ………………………………9分
则
 ,
,
即 ,
,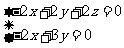
取x=3,则y=2,z=1,∴
面BCF的一个法向量为 ……………………………12分
……………………………12分
则cos<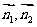 >=
>=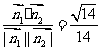 …………………………………………13分
…………………………………………13分
由于所求二面角D-BF-C的平面角为钝角,所以此二面角的余弦值为-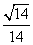 ……………14分
……………14分
(法二)作DH⊥EF于H,作HM⊥BF,连DM。
由三垂线定理知 BF⊥DM,∴∠DMH是二面角D-BF-C的平面角的补角。…………………………9分
由△HMF∽△EBF,知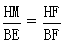 ,而HF=1,BE=2,
,而HF=1,BE=2, ,∴HM=
,∴HM=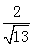 。
。
又DH=2,
∴在Rt△HMD中,tan∠DMH=- ,
,
因∠DMH为锐角,∴cos∠DMH=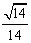 , ………………………………13分
, ………………………………13分
而∠DMH是二面角D-BF-C的平面角的补角,
故二面角D-BF-C的余弦值为-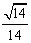 。 ………………………………14分
。 ………………………………14分
44、(广东省四校联合体第一次联考)
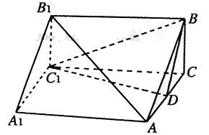 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
(1)求证:AB1//面BDC1;
(2)求二面角C1-BD-C的余弦值;
(3)在侧棱AA1上是否存在点P,使得
CP⊥面BDC1?并证明你的结论.
(1)连接B1C,交BC1于点O,则O为B1C的中点,
∵D为AC中点 ∴OD∥B1A
又B1A 平面BDC1,OD
平面BDC1,OD 平面BDC1
平面BDC1
∴B1A∥平面BDC1
(2)∵AA1⊥面ABC,BC⊥AC,AA1∥CC1
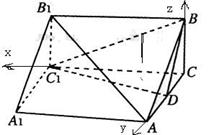 ∴CC1⊥面ABC
∴CC1⊥面ABC
则BC⊥平面AC1,CC1⊥AC
如图建系 则C1(3,0,0) B(0,0,2) D(0,1,0) C(0,0,0)
∴
设平面C1DB的法向量为
则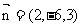
又平面BDC的法向量为
∴二面角C1-BD-C的余弦值:cos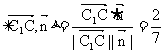
(Ⅲ)设P(h,2,0) 则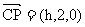
若CP⊥面BDC1 则 即(h,2,0)=λ(2,-6,3)
即(h,2,0)=λ(2,-6,3)
此时λ不存在
∴在侧棱AA1上不存在点P,使得CP⊥面BDC1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com