
23、(北京市丰台区2008年4月高三统一练习一)已知直线m、l,平面α、β,且m⊥α, l  β,给出下列命题:①若α∥β,则m⊥l;②若α⊥β,则m∥l;③若m⊥l,则α∥β;④若m∥l,则α⊥β.其中正确命题的个数是
β,给出下列命题:①若α∥β,则m⊥l;②若α⊥β,则m∥l;③若m⊥l,则α∥β;④若m∥l,则α⊥β.其中正确命题的个数是
(A)1 (B)2
(C)3 (D)4
答案:B
22、(北京市东城区2008年高三综合练习二)已知正四面体A-BCD,动点P在△ABC内,且点P到平面BCD的距离与点P到点A的距离相等,则动点P的轨迹为 ( )
A.椭圆的一部分 B.双曲线的一部分 C.抛物线的一部分 D.一条线段
答案:A
21、(北京市东城区2008年高三综合练习二)直线a∥平面α的一个充分条件是( )A.存在一条直线b,b∥α,a∥b B.存在一个平面β,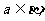 α∥β
α∥β
C.存在一个平面β,a∥β,α∥β D.存在一条直线b,b α,a∥b
α,a∥b
答案:B
20、(北京市东城区2008年高三综合练习一)长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )
A.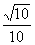 B.
B.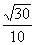 C.
C.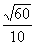 D.
D.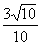
答案:B
19、(北京市崇文区2008年高三统一练习一)如图,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1上的动点,则直线NO、AM的位置关系是( )
A.平行 B.相交
C.异面垂直 D.异面不垂直
答案:C
18、(北京市朝阳区2008年高三数学一模)设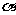 、
、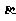 、
、 是三个不同的平面,a、b是两条不同的直线,给出下列4个命题:
是三个不同的平面,a、b是两条不同的直线,给出下列4个命题:
①若a∥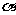 ,b∥
,b∥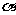 ,则a∥b; ②若a∥
,则a∥b; ②若a∥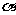 ,b∥
,b∥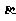 ,a∥b,则
,a∥b,则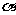 ∥
∥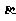 ;
③若a⊥
;
③若a⊥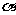 ,b⊥
,b⊥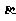 ,a⊥b,则
,a⊥b,则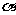 ⊥
⊥ ;④若a、b在平面
;④若a、b在平面 内的射影互相垂直,则a⊥b. 其中正确命题是
内的射影互相垂直,则a⊥b. 其中正确命题是
A. ③ B. ④ C. ①③ D. ②④
 答案:A
答案:A
16、(安徽省淮南市2008届高三第一次模拟考试)已知α、β是平面,m、n是直线,则下命题不正确的是( ▲ ).
A.若m∥n , m⊥α, 则n⊥α B. 若,m⊥α, m⊥β, 则α∥β
C.若m⊥α, m∥n, n β,
则α⊥β D. .若m∥α, α ∩β=n则m∥n
β,
则α⊥β D. .若m∥α, α ∩β=n则m∥n
答案:D
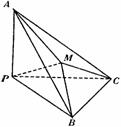 17、9.(安徽省巢湖市2008届高三第二次教学质量检测)如图,在三棱锥P-ABC中,
17、9.(安徽省巢湖市2008届高三第二次教学质量检测)如图,在三棱锥P-ABC中,
∠APB=∠BPC=∠APC=90°,M在△ABC内,
∠MPA=60°,∠MPB=45°,则∠MPC的度数为( )
A.30° B.45° C.60° D.75°
答案:C
15、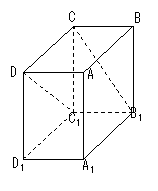 (安徽省淮南市2008届高三第一次模拟考试)在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为( ▲ )
(安徽省淮南市2008届高三第一次模拟考试)在长方体ABCD-A1B1C1D1中,B1C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成的角的余弦值为( ▲ )
A.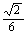 B.
B. 
C. 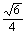 D.
D.
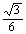
答案:C
14、(四川省成都市新都一中高2008级12月月考)一个四面体的所有棱长都为,四个顶点在同一球面上,则此球的表面积为( )
A、3π B、4π C、3π D、6π
本题考查正多面体、球的基本概念和性质,以及他们相互之间的关系,常见几何量的计算
解法1 如图,点O为球心,OA、OB、OC、OD都是球的半径,因为ABCD是正四面体,所以这四条半径的两两夹角彼此相等,设其大小为θ.
由空间中的一点O,引四条射线,两两的夹角都等于θ,则有
<θ<
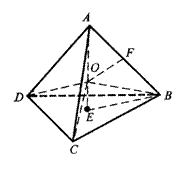
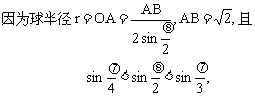
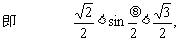
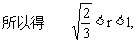
因此球的表面积S=4πr2满足π<S<4π
据此,可排除选项B、C和D,应取A作答.
解法2 联想棱长为1的正方体ABCD-A1B1C1D1,则四面体ACB1D1的棱长都为,它的外接球也是正方体的外接球,其半径为正方体对角线长的一半,即有r=,故所求球面积为S=3π.
答案 A
13、(四川省成都市新都一中高2008级12月月考)已知一个四面体有五条棱长都等于2,则该四面体的体积最大值为( )
A、 B、 C、1 D、2
本题主要考查空间几何体的基本性质,最值.
解析:由于有五条棱长都等于2,则四面体中至少有两个面是边长为2的正三角形,以其中一个为底面,则当另一个正三角形所在平面与它垂直时,四面体体积最大.
此时,底面积为,高为,
所以,体积为××=1
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com