
64、(湖北省鄂州市2008年高考模拟)在正三棱锥 中,
中,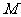 、
、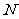 分别是棱
分别是棱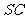 、
、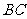 的中点,且
的中点,且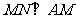 ,若侧棱
,若侧棱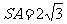 ,则正三棱锥
,则正三棱锥 外接球的表面积是( )
外接球的表面积是( )
A.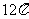 B.
B.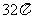 C.
C.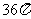 D.
D.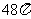
答案:C 正三棱锥对棱互相垂直,即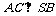 ,又SB∥MN,且
,又SB∥MN,且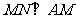 ,
∴
,
∴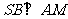 ,从而
,从而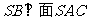 . ∴
. ∴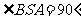 ,以
,以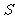 为顶点,将三棱锥补成一个正方体,故球的直径
为顶点,将三棱锥补成一个正方体,故球的直径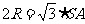 ,即
,即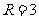 ,∴
,∴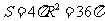 ,故选C.
,故选C.
[总结点评]本题主要考查线面的位置关系,几何体与球的切接问题,球的表面积公式,关键利用四面体的性质及通过补形求球的半径.
63、(湖北省鄂州市2008年高考模拟)在正三棱锥中,相邻两侧面所成二面角的取值范围是( )
A.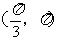 B.
B.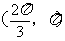 C.(0,
C.(0, ) D.
) D.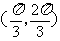
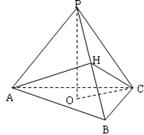 答案:A 方法一:观察正三棱锥P–ABC,O为底面中心,不妨将底面正△ABC固定,顶点P运动,相邻两侧面所成二面角为∠AHC.当PO→0时,面PAB→△OAB,面PBC→△OBC,∠AHC→π,当PO→+∞时,
答案:A 方法一:观察正三棱锥P–ABC,O为底面中心,不妨将底面正△ABC固定,顶点P运动,相邻两侧面所成二面角为∠AHC.当PO→0时,面PAB→△OAB,面PBC→△OBC,∠AHC→π,当PO→+∞时,
∠AHC→∠ABC=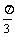 .故
.故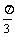 <∠AHC <π,
<∠AHC <π,
选A.
方法二:不妨设AB=2,PC= x,
则x > OC =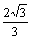 .等腰△PBC中,
.等腰△PBC中,
S△PBC =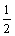 x·CH =
x·CH =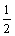 ·2·
·2·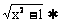 CH =
CH =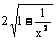 ,等腰△AHC中,sin
,等腰△AHC中,sin .由x>
.由x>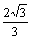 得
得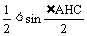 <1,∴
<1,∴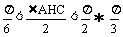 <∠AHC<π.
<∠AHC<π.
[总结点评]本题主要考查多面体、二面角等基础知识,分析问题与解决问题的能力,注重考查我们对算法算理的理解.
62、(湖北省三校联合体高2008届2月测试)关于直线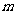 ,
,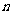 与平面
与平面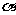 ,
,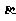 ,有以下四个命题:
,有以下四个命题:
①若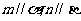 且
且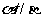 ,则
,则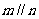 ; ②若
; ②若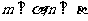 且
且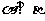 ,则
,则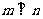 ;
;
③若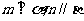 且
且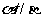 ,则
,则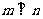 ; ④若
; ④若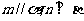 且
且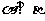 ,则
,则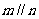 .
.
其中真命题的序号是 ( )
A.①② B.③④ C.①④ D.②③
答案:D
61、(湖北省八校高2008第二次联考)一个凸多面体各面都是三角形,各顶点引出的棱的条数均为4,则这个多面体只能是( )
A.四面体 B.六面体 C.七面体 D.八面体
答案:D
60、(湖北省八校高2008第二次联考)二面角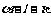 为
为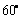 ,A,B是棱
,A,B是棱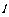 上的两点,AC,BD分别在半平面
上的两点,AC,BD分别在半平面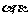 内,
内,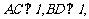 且
且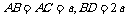 ,则
,则 的长为( )
的长为( )
A.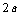 B.
B.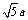 C.
C.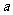 D.
D.
答案:A
59、(黑龙江省哈师大附中2008届高三上期末)设直线m,n和平面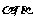 ,对下列命题:
,对下列命题:
(1)若 ;
;
(2)若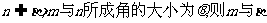 所成角的大小也为
所成角的大小也为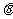 ;
;
(3)若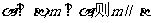 ;
;
(4)若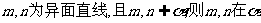 上的射影为两条直交直线,其中正确命题的个数为( )
上的射影为两条直交直线,其中正确命题的个数为( )
A.2个 B.1个 C.3个 D.4个
答案:B
58、(黑龙江省哈尔滨九中2008年第三次模拟考试)有如下一些说法,其中正确的是
①若直线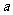 ∥
∥ ,
, 在面
在面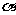 内,则
内,则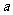 ∥
∥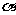 ;②若直线
;②若直线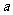 ∥
∥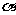 ,
, 在面
在面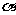 内,则
内,则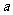 ∥
∥ ;
;
③若直线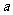 ∥
∥ ,
,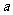 ∥
∥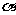 ,则
,则 ∥
∥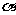 ;④若直线
;④若直线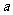 ∥
∥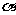 ,
, ∥
∥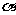 ,则
,则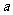 ∥
∥ .
.
A.①④ B.①③ C.② D.均不正确
答案:D
57、(黑龙江省哈尔滨九中2008年第三次模拟考试)直线 与平面
与平面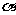 成45°角,若直线
成45°角,若直线 在
在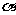 内的射影与
内的射影与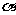 内的直线
内的直线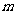 成45°角,则
成45°角,则 与
与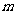 所成的角是( )
所成的角是( )
A.30° B.45° C. 60° D.90°
答案:C
56、(河南省濮阳市2008年高三摸底考试)在直三棱柱A1B1C1-ABC中,∠BAC=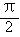 ,AB=AC=AA1=1.已知G与E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围为( )
,AB=AC=AA1=1.已知G与E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点).若GD⊥EF,则线段DF的长度的取值范围为( )
A.[ 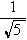 ,1) B.[
,1) B.[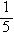 ,2)
C.[1,
,2)
C.[1,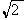 ) D.[
) D.[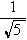 ,
,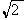 )
)
答案:A
55、(河南省开封市2008届高三年级第一次质量检)从P点出发三条射线PA,PB,PC两两成60°,且分别与球O相切于A,B,C三点,若球的体积为,则OP的距离为( )
A. B. C. D.2
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com