
3.已知数列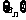 中,
中,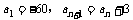 ,那么
,那么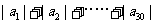 等于( )
等于( )
A、-495 B、765 C、1080 D、3105
2.数列{an}的前n项和Sn=3n-2n2 (n∈N),当n>2时有( )
A.Sn>na1>nan B.Sn< nan<na1 C.na1<Sn<nan D.nan<Sn<na1
例12. 设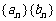 是两个数列,点
是两个数列,点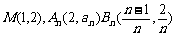 为直角坐标平面上的点.
为直角坐标平面上的点.
(1)对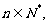 若三点
若三点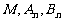 共线,求数列
共线,求数列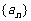 的通项公式;
的通项公式;
(2)若数列{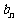 }满足:
}满足: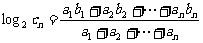 ,其中
,其中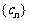 是第三项为8,公比为4的等比数列.求证:点列
是第三项为8,公比为4的等比数列.求证:点列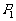 (1,
(1,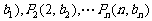 在同一条直线上,并求此直线的方程.
在同一条直线上,并求此直线的方程.
例13. 已知曲线y=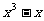 ,过曲线上一点
,过曲线上一点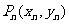 (异于原点)作切线
(异于原点)作切线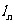 。
。
(1)求证:直线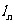 与曲线y=
与曲线y=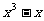 交于另一点
交于另一点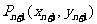 ;
;
(2)在(1)的结论中,求出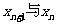 的递推关系。若
的递推关系。若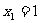 ,求数列
,求数列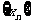 的通项公式;
的通项公式;
(3)在(2)的条件下,记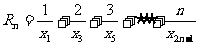 ,问是否存在自然数m,M,使得不等式m<Rn<M对一切
,问是否存在自然数m,M,使得不等式m<Rn<M对一切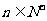 恒成立,若存在,求出M-m的最小值;否则请说明理由。
恒成立,若存在,求出M-m的最小值;否则请说明理由。
变式:
由坐标原点O向曲线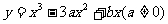 引切线,切于O以外的点P1
引切线,切于O以外的点P1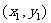 ,再由P1引此曲线的切线,切于P1以外的点P2
,再由P1引此曲线的切线,切于P1以外的点P2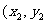 ),如此进行下去,得到点列{ Pn
),如此进行下去,得到点列{ Pn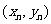 }.
}.
求:(1)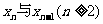 的关系式;(2)数列
的关系式;(2)数列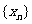 的通项公式
的通项公式
反馈练习:
1.已知数列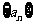 的前n项和
的前n项和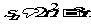 ,那么这个数列中的奇数项依照原来的顺序构成的数列的通项公式是( )
,那么这个数列中的奇数项依照原来的顺序构成的数列的通项公式是( )
A.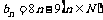 B.
B.
C.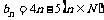 D.
D. 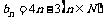
例11. 某地为了防止水土流失,植树造林,绿化荒沙地,每年比上一年多植相同亩数的林木,但由于自然环境和人为因素的影响,每年都有相同亩数的土地沙化,具体情况为下表所示:
|
|
1998年 |
1999年 |
2000年 |
|
新植亩数 |
1000 |
1400 |
1800 |
|
沙地亩数 |
25200 |
24000 |
22400 |
而一旦植完,则不会被沙化。问:(1)每年沙化的亩数为多少?(2)到那一年可绿化完全部荒沙地?
变式:
某公司按现有能力,每月收入为70万元,公司分析部门测算,若不进行改革,入世后因竞争加剧收入将逐月减少.分析测算得入世第一个月收入将减少3万元,以后逐月多减少2万元,如果进行改革,即投入技术改造300万元,且入世后每月再投入1万元进行员工培训,则测算得自入世后第一个月起累计收入Tn与时间n(以月为单位)的关系为Tn=an+b,且入世第一个月时收入将为90万元,第二个月时累计收入为170万元,问入世后经过几个月,该公司改革后的累计纯收入高于不改革时的累计纯收入.
例9.已知函数f(x)=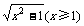
(1)求f(x)的反函数f-1 (x)的表达式;
(2)数列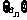 中,a1 =1;an =f-1 (an-1) (
中,a1 =1;an =f-1 (an-1) ( 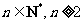 ),如果bn =
),如果bn =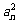 (nÎN),求数列
(nÎN),求数列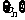 的通项公式及前n项和Sn;
的通项公式及前n项和Sn;
(3)如果g(n)=2Sn-17n,求函数g(x) (xÎR)在区间[t,t+2] (tÎR)上的最小值h(t)的表达式。
例10. 函数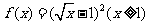 的反函数为
的反函数为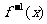 ,数列
,数列 满足:
满足: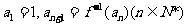 ,数列
,数列 满足:
满足: ,
,
(1)求数列 和
和 的通项公式;
的通项公式;
(2)记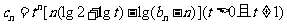 ,若对任意的
,若对任意的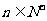 ,恒有
,恒有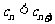 成立,求实数
成立,求实数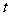 的取值范围.
的取值范围.
变式:
已知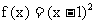 ,
,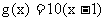 ,数列
,数列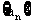 满足
满足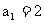 ,
,
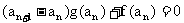 ,
, 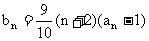 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)当n取何值时,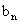 取最大值,并求出最大值;
取最大值,并求出最大值;
(III)若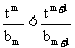 对任意
对任意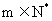 恒成立,求实数
恒成立,求实数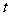 的取值范围.
的取值范围.
例7. 若函数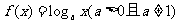 ,数列
,数列  成等差数列.
成等差数列.
(1)求数列 的通项
的通项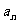 ;
;
(2)若 ,令
,令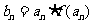 ,求数列
,求数列 前
前 项和
项和 ;
;
(3)在(2)的条件下对任意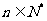 ,都有
,都有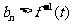 ,求实数
,求实数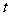 的取值范围。
的取值范围。
例8. 设数列{an}的首项a1=1,前n项和Sn满足关系式:3tSn-(2t+3)Sn-1=3t (t>0,n=2,3,4…)
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使b1=1,bn=f(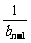 )(n=2,3,4…),求数列{bn}的通项bn;
)(n=2,3,4…),求数列{bn}的通项bn;
(3)求和:b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1
变式:
已知二次函数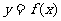 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为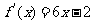 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点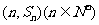 均在函数
均在函数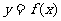 的图像上.
的图像上.
(1) 求数列 的通项公式;
的通项公式;
(2) 设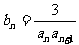 ,
,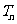 是数列
是数列 的前n项和,求使得
的前n项和,求使得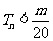 对所有
对所有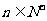 都成立的最小正整数m.
都成立的最小正整数m.
 例5. 如图,将圆分成
例5. 如图,将圆分成 个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为
个区域,用3种不同颜色给每一个区域染色,要求相邻区域颜色互异,把不同的染色方法种数记为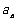 。求
。求
(Ⅰ)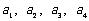 ;
;
(Ⅱ)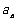 与
与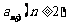 的关系式;
的关系式;
(Ⅲ)数列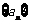 的通项公式
的通项公式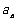 ,并证明
,并证明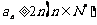 。
。
例6. 在数列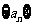 中,
中,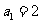 ,
,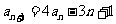 ,
,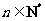 .
.
(1)证明数列 是等比数列;
是等比数列;
(2)求数列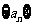 的前
的前 项和
项和 ;
;
(3)证明不等式 ,对任意
,对任意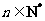 皆成立.
皆成立.
变式:
数列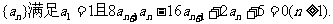 记
记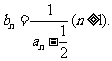
(1)求b1、b2、b3、b4的值;(2)求数列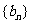 的通项公式及数列
的通项公式及数列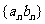 的前n项和
的前n项和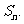
2.设 是数列
是数列 (
(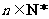 )的前
)的前 项和,
项和,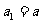 ,且
,且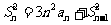 ,
,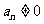 ,
,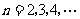 .
.
(I)证明:数列 (
(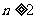 )是常数数列;
)是常数数列;
(II)试找出一个奇数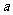 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列 (
(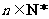 )中的所有项都是数列
)中的所有项都是数列 中的项,并指出
中的项,并指出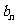 是数列
是数列 中的第几项.
中的第几项.
例3.已知数列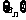 的前n项和为Sn,满足条件
的前n项和为Sn,满足条件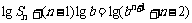 ,其中b>0且b
,其中b>0且b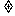 1。
1。
(1)求数列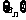 的通项an;(2)若对
的通项an;(2)若对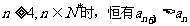 ,试求b的取值范围。
,试求b的取值范围。
例4. 已知数列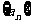 的前
的前 项和为
项和为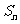 ,若
,若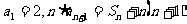 ,
,
(1)证明数列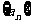 为等差数列,并求其通项公式;
为等差数列,并求其通项公式;
(2)令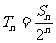 ,①当
,①当 为何正整数值时,
为何正整数值时,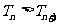 ;②若对一切正整数
;②若对一切正整数 ,总有
,总有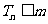 ,求
,求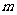 的取值范围。
的取值范围。
变式:
1.在等差数列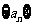 中,
中,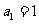 ,前
,前 项和
项和 满足条件
满足条件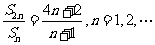 ,
,
(Ⅰ)求数列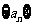 的通项公式;
的通项公式;
(Ⅱ)记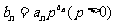 ,求数列
,求数列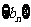 的前
的前 项和
项和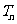 。
。
例1.数列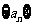 中,
中,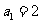 ,
,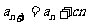 (
(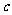 是常数,
是常数,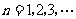 ),且
),且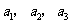 成公比不为
成公比不为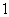 的等比数列。(1)求
的等比数列。(1)求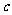 的值;(2)求
的值;(2)求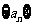 的通项公式。
的通项公式。
例2.若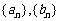 都是各项为正的数列,对任意的正整数
都是各项为正的数列,对任意的正整数 都有
都有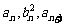 成等差数列
成等差数列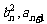 ,
,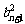 成等比数列。
成等比数列。
(1)试问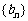 是否是等差数列?为什么?
是否是等差数列?为什么?
(2)求证:对任意的正整数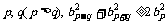 成立;
成立;
(3)如果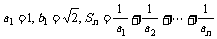 ,求
,求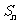 。
。
变式:
数列{an}中,a1=8,a4=2且满足an+2=2an+1-an,(n∈N*)。
(1)求数列{an}的通项公式;
(2)设Sn=|a1|+|a2|+…+|an|,求Sn;
(3)设bn=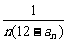 (n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn>
(n∈N*),Tn=b1+b2+……+bn(n∈N*),是否存在最大的整数m,使得对任意n∈N*均有Tn>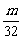 成立?若存在,求出m的值;若不存在,说明理由。
成立?若存在,求出m的值;若不存在,说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com