3.(★★★★)如图21-6，是钾、氧两元素形成的一种晶体在高温时的立体结构。该结构是具有代表性的最小重复单元。试问：每个钾离子周围最近且距离相等的钾离子、氧离子数目分别是________和________。

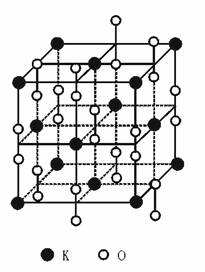
图21-6

2.(★★★★)图21-5所示结构是干冰晶体中具有代表性的最小重复单元。则每个CO₂分子周围距离相等且最近的CO₂分子数目为(　 )

A.6　　　　　　　　　　　　　　　 B.8　　　　　　　　　　　　　　　 C.10　　　　　　　　　　　　　　　　　 D.12

1.(★★★)石墨晶体结构如图21-4所示。每个C原子周围离它最近且距离相等的C原子个数是(　 )

A.3　　　　　　　　　　　　　　　 B.4　　　　　　　　　　　　　　　 C.5　　　　　　　　　　　　　　　 D.6

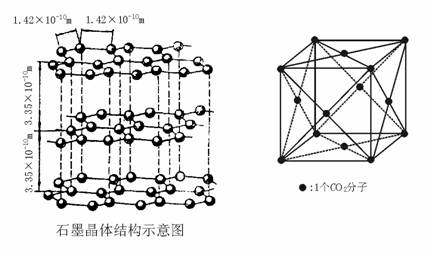
图21-4　　　　　　　　　　　　　 图21-5　

对于这类问题的解决，一定要看清条件，按照所要解决的问题，利用条件，关键在于能否找到条件与所求的联系。这类问题没有现成的方法，它所考查的是同学们的发散思维。

例9、已知函数f ( x )满足f ( ab ) =　 f ( a ) + f ( b )，且f ( 2 ) = p, f ( 3 ) = q,则f ( 36 ) =　 ?

[分析]该题要求的是f ( 36 ),而条件中给我们f ( ab ) = ……，自然会想到，36能拆成什么的乘积了。

例10、已知f ( x ) = 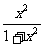，那么f ( 1 ) + f ( 2) + f (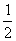) + f ( 3 ) + f( 　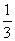) 　+ f ( 4 )　 + f ()

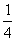例11、若上题要求： f ( 1 ) + f ( 2 ) + f (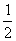) + …… + f ( n ) + f (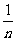) + …… + f ( 2003 ) + f () 　　　　

对于复合函数的解析式的求法，虽然种类很多，在这里重点介绍配凑法和换元法，详细内容请参阅《教学周刊》第6期。

(1)配凑法

　 若已知f [ g ( x ) ] = F ( x )是关于x的函数，可以把F ( x )表示g ( x )的复合函数形式，然后用x替换g ( x )，即可得到f ( x )的解析式。

例5、已知f (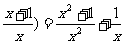，求f ( x )的解析式。

例6、已知f ( x + 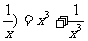,求f ( x )的解析式。

(2)换元法

　 若已知f [ g ( x ) ]的表达式，可以令g ( x ) = t，从中解出x再将x代入f [ g ( x ) ]的表达式中，这样f [ g ( x ) ]就表示成关于t 的函数，即得函数f ( x )的解析式。　

例7、已知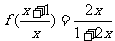　 ( x > 0 )求f ( x )的解析式。

例8、用换元法看看例5，例6能否适用。

(1)若f(x)的定义域为a ≤ x ≤ b,则f [ g ( x ) ] 中的a ≤ g ( x ) ≤ b ，从中解得x的范围，即为f [g ( x )]的定义域。

例1、y = f ( x ) 的定义域为[ 0 ， 1 ]，求f ( 2x + 1 )的定义域。

例2、已知f ( x )的定义域为(0，1)，求f ( x ²)的定义域。

(2)若f [ g ( x ) ]的定义域为(m , n)则由m < x < n 确定出g ( x )的范围即为f ( x )的定义域。

C.[H]和ATP　　 D.184条、0条

例3、已知函数f ( 2x + 1 )的定义域为(0，1)，求f ( x ) 的定义域。

(3)由f [ g ( x ) ] 的定义域，求得f ( x )的定义域后，再求f [ h ( x ) ]的定义域。

例4、已知f ( x + 1 )的定义域为[-2 ，3],求f ( 2x ² – 2 ) 的定义域。

对于这类问题的解决，一定要看清条件，按照所要解决的问题，利用条件，关键在于能否找到条件与所求的联系。这类问题没有现成的方法，它所考查的是同学们的发散思维。

例9、已知函数f ( x )满足f ( ab ) =　 f ( a ) + f ( b )，且f ( 2 ) = p, f ( 3 ) = q,则f ( 36 ) =　 ?

[分析]该题要求的是f ( 36 ),而条件中给我们f ( ab ) = ……，自然会想到，36能拆成什么的乘积了。

对于复合函数的解析式的求法，虽然种类很多，在这里重点介绍配凑法和换元法，详细内容请参阅《教学周刊》第6期。

(1)配凑法

　 若已知f [ g ( x ) ] = F ( x )是关于x的函数，可以把F ( x )表示g ( x )的复合函数形式，然后用x替换g ( x )，即可得到f ( x )的解析式。

例5、已知f (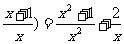，求f ( x )的解析式。

　 答案：f(x)= x ²

例6、已知f ( x + 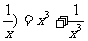,求f ( x )的解析式。

　 答案：f(x)= x ³-2x-1

(2)换元法

　 若已知f [ g ( x ) ]的表达式，可以令g ( x ) = t，从中解出x再将x代入f [ g ( x ) ]的表达式中，这样f [ g ( x ) ]就表示成关于t 的函数，即得函数f ( x )的解析式。　

例7、已知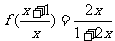　 ( x > 0 )求f ( x )的解析式。

答案： 2 / (x-3)

例8、用换元法看看例5，例6能否适用。

　 答案：f(x)= x ²　 f(x)= x ³-2x-1

(1)若f(x)的定义域为a ≤ x ≤ b,则f [ g ( x ) ] 中的a ≤ g ( x ) ≤ b ，从中解得x的范围，即为f [g ( x )]的定义域。

例1、y = f ( x ) 的定义域为[ 0 ， 1 ]，求f ( 2x + 1 )的定义域。

　 答案： [-1/2 ，0 ]

例2、已知f ( x )的定义域为(0，1)，求f ( x ²)的定义域。

　 答案： [-1 ，1]

(2)若f [ g ( x ) ]的定义域为(m , n)则由m < x < n 确定出g ( x )的范围即为f ( x )的定义域。

例3、已知函数f ( 2x + 1 )的定义域为(0，1)，求f ( x ) 的定义域。

　 　答案： [ 1 ，3]

(3)由f [ g ( x ) ] 的定义域，求得f ( x )的定义域后，再求f [ h ( x ) ]的定义域。

例4、已知f ( x + 1 )的定义域为[-2 ，3],求f ( 2x ² – 2 ) 的定义域。

　 答案：[-√3/2 ，-√3]∪[√3/2 ，√3]

如果y是u的函数，而u是x的函数，即y = f ( u ), u = g ( x ) ,那么y关于x的函数y = f [g ( x ) ]叫做函数f 与 g 的复合函数，u 叫做中间变量。

注意：复合函数并不是一类新的函数，它只是反映某些函数在结构方面的某种特点，因此，根据复合函数结构，将它折成几个简单的函数时，应从外到里一层一层地拆，注意不要漏层。

另外，在研究有关复合函数的问题时，要注意复合函数的存在条件，即当且仅当g ( x )的值域与f ( u )的定义域的交集非空时，它们的复合函数才有意义，否则这样的复合函数不存在。

例：f ( x + 1 ) = (x + 1)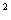 可以拆成y = f ( u ) = u² , u = g ( x ) , g ( x ) = x + 1 ,即可以看成f ( u ) = u² 与g ( x ) = x + 1 两个函数复合而成。